《医学物理学》课程教学资源（PPT课件）静电场习题课

静电场习题课 ★基本概念： L 5E6-24 ★基本定理： ∮E●i=0 ★基本计算： E u u. W A.=q(u.-u,)=W.-W,=qfE.di

静电场习题课 ★基本概念： E  u ★基本定理：  • =  s qi E ds 0 1     E • dl = 0   ★基本计算： E  u uab W a = − = − =  • b a a b a b a b A q( u u ) W W q E dl  

本章内容要点： 静电场的场量 点电荷 电场叠加性 Eu关系 ∑E, 4π6r2 E= ∫E u,-Eod u ∑4 E =-Yu 4π。 a a= ∫du

静电场的场量 点电荷 电场叠加性 E  u 关系 q0 F E   =   = = • a a a E dl q W u   0 2 0 4 0 r r q E    = r q u 4 0 = E =   Ei   dE  ui  du   = • P P u E dl   E = −u  u = 本章内容要点：

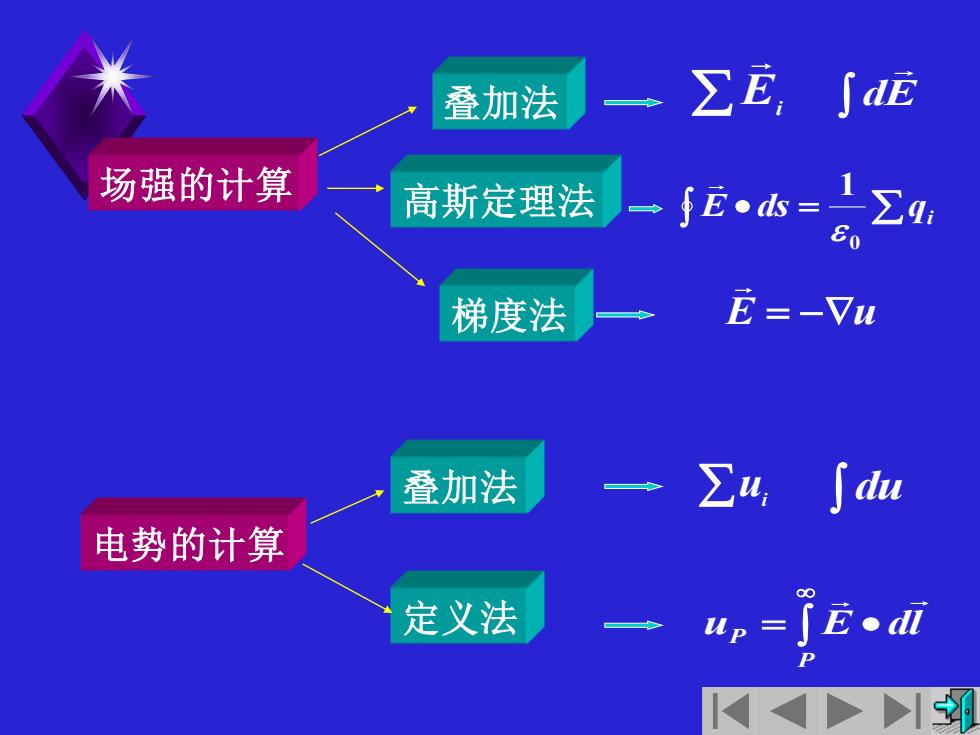
叠加法 ∑E,∫dE 场强的计算 高斯定理法 手Ew=Σa 梯度法 E =-Yu 叠加法 一∑4，∫du 电势的计算 定义法 一u=了E0

场强的计算 电势的计算 叠加法 高斯定理法 梯度法 叠加法 定义法  Ei   dE   E • ds = qi 0 1   E = −u  ui  du   = • P P u E dl  

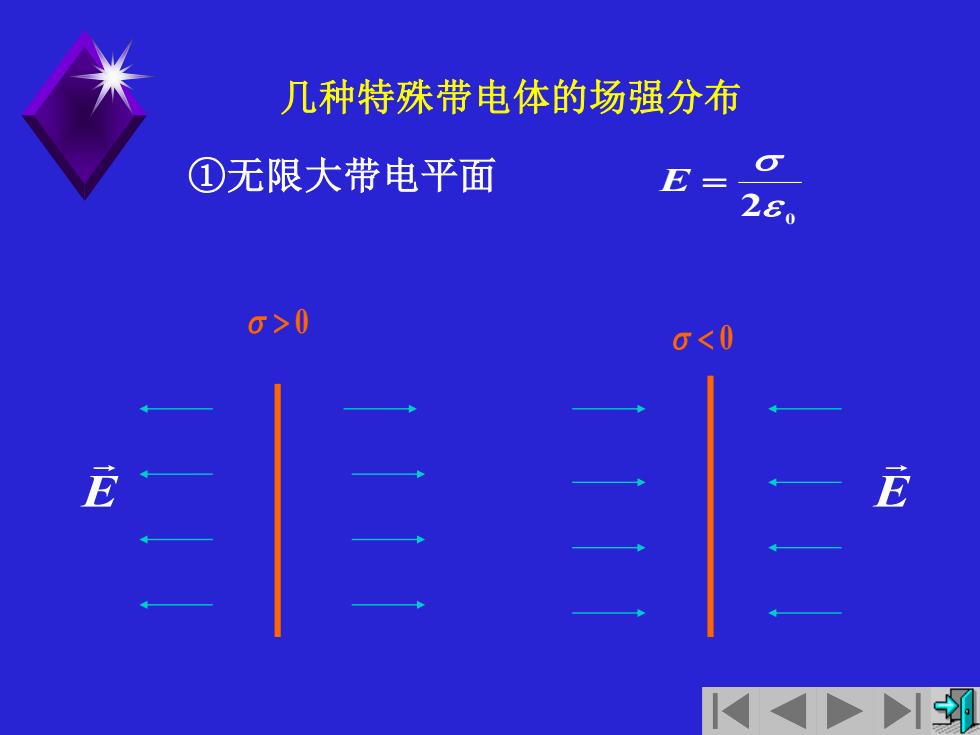
几种特殊带电体的场强分布 ①无限大带电平面 E- 20 g>0 g<0

①无限大带电平面 2 0  E =   0 E    0 E  几种特殊带电体的场强分布

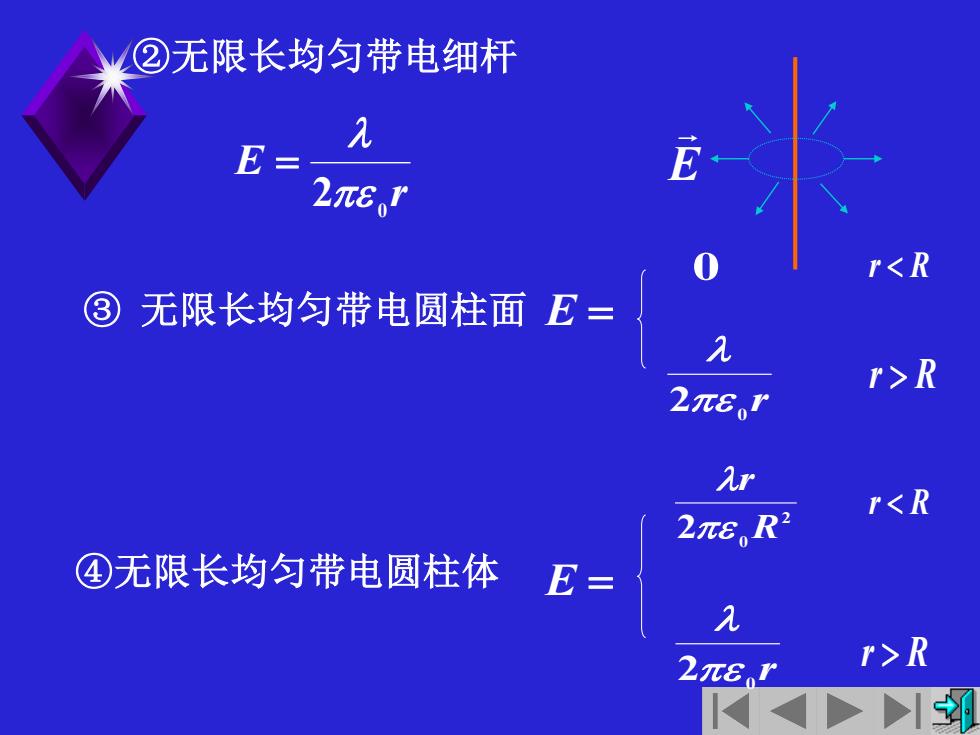
②无限长均匀带电细杆 E= 2π6，T rR 2π8，r Ar 2π6。R2 rR

②无限长均匀带电细杆 r E 2 0  = ④无限长均匀带电圆柱体 ③ 无限长均匀带电圆柱面 r 2 0  E = 0 r  R r  R 2 2 0 R r   r 2 0  E = r  R r  R E 

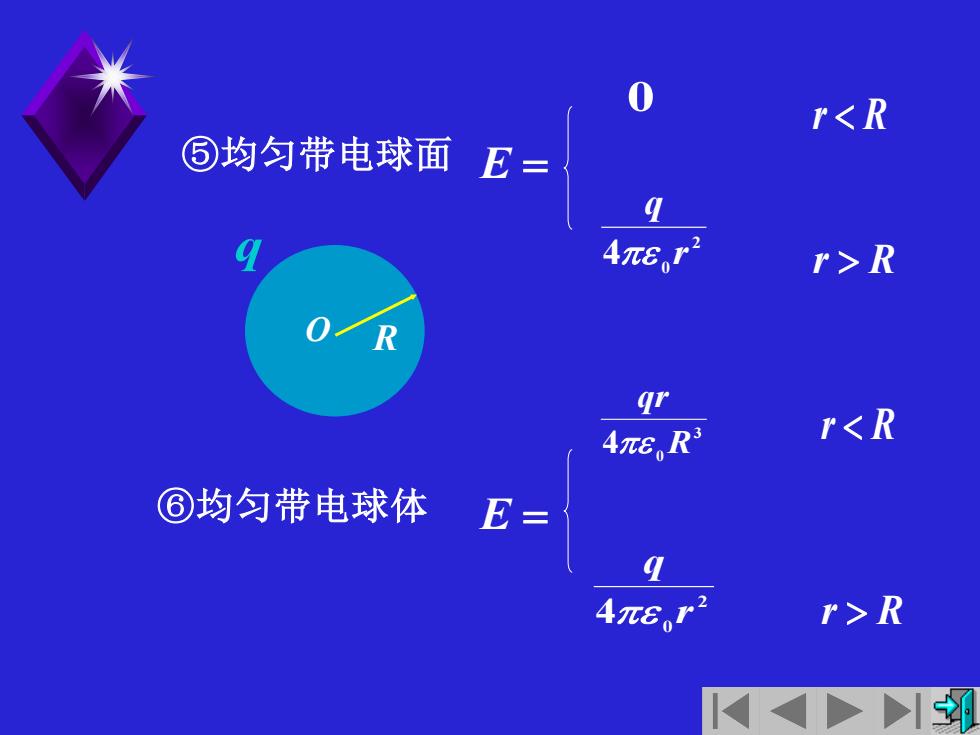
rR R gr 4π6R rR

⑤均匀带电球面 ⑥均匀带电球体 2 4 0 r q  E = 0 r  R r  R 3 4 0 R qr  2 4 0 r q  E = r  R r  R O R q

静电场中的导体 导体静电平衡条件 电荷分布 场强分布 二静电场中的电介质 oE 真空中 1.D= 806,E 介质中 2.高斯定理 fD·S=∑q

一.静电场中的导体 导体静电平衡条件 电荷分布 场强分布 二.静电场中的电介质 1. D =  E  0  r E   0 真空中 介质中 2. 高斯定理  • =  S D dS qi  

三 电容 电容器 五.求C的方法 孤立导体 C= 定义法 u 电容器 能量法 C= UA一B 四电场能量 1.电容器 O: W= 2.电场 w-fwav

三. 电容 电容器 孤立导体 u q C = 电容器 uA uB q C − = 四.电场能量 1. 电容器 Cu Qu C Q W 2 1 2 1 2 2 2 = = = 2.电场 =  V W wdV 2 2 1 w = E 五. 求 C 的方法 定义法 能量法

补偿法求场强 1带电圆弧 已知：R=50cm d 2cm q=3.12×10-9C 求：E。 解：圆弧 = 2元R 带电园环 + 园弧上电荷 0处的E=0 空隙 点电荷 d 0处的E2=4玩eR2=4rER d ∴.E。=E2= AnenR2

Eo  补偿法求场强 1.带电圆弧 q . C 9 3 12 10− d = 2cm =  o R d 求: Eo  解:圆弧 R q   2 = 空隙 0 o 处的 E1 = −  +  + 园弧上电荷 带电园环 点电荷 2 0 2 0 2 4 4 R d R q E    =  o 处的 = 2 0 2 4 R d Eo E    = = 已知: R = 50cm

2.求两无限长同轴圆柱面的电势差 已知：+2-入R2R 解：场强分布 - 兄 2πeor RR 电势差 n=了Eh= T€0

2.求两无限长同轴圆柱面的电势差 −  R2 R1 已知: +  R2 解: 场强分布 −  +  R1 r 2 0  E = 1 R2 R  r  0 1 R2 r  R r  =  = 2 1 1 2 0 1 12 2 R R R R u Edr ln   电势差