
量子 第十五章量子力学基础 (光的量子性) 、 学习本章后,我们应该: 1.掌握热辐射、辐出度、黑体等概念; 2.掌握斯蒂芬-玻尔兹曼定律、维恩位移定 律; 3.理解黑体辐射能量分布曲线、普朗克公 式、光电效应、 康普顿效应; 结束 二、授课重点: 黑体辐射、 斯蒂芬一玻尔兹曼定律、维 恩位移定律。 三、学时数: 2-3学时 2010.11. 10:1:1d 后页
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 1 第十五章 量子力学基础(光的量子性) 一、学习本章后,我们应该: 1.掌握热辐射、辐出度、黑体等概念; 2.掌握斯蒂芬-玻尔兹曼定律、维恩位移定 律; 3.理解黑体辐射能量分布曲线、普朗克公 式、光电效应、康普顿效应; 二、授课重点: 黑体辐射、斯蒂芬-玻尔兹曼定律、维 恩位移定律。 三、学时数:2-3学时

量 学 基 第一节黑体辐射 (红外、可见光波段的辐射) 热辐射(Thermal radiation) 光电 1.热辐射:由分子原子热运动引起的辐射 现象或与温度有关的辐射。 2.热辐射产生的原因:物体中的原子不停 的作热运动?在剧烈的碰撞中,总是不断 结束 有原子吸收动能进入激发状态,处在激发 态上原子不稳定,跃迁!多余能量以电磁 波的形式辐射,形成热辐射。 问题与思考:热辐射的实质? 返回前页 9 后页
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 2 第一节 黑体辐射(红外、可见光波段的辐射) 1.热辐射:由分子原子热运动引起的辐射 现象或与温度有关的辐射。 2.热辐射产生的原因:物体中的原子不停 的作热运动?在剧烈的碰撞中,总是不断 有原子吸收动能进入激发状态,处在激发 态上原子不稳定,跃迁! 多余能量以电磁 波的形式辐射,形成热辐射。 问题与思考:热辐射的实质? 一、热辐射(Thermal radiation) :

量子 3.性质 (1)物体的温度不同辐射的能量不同(电磁波 的波长不同)。或者说 热 光电狼 注意:低温物体的辐射远红外线,不易觉察; 效应 高温物体的辐射可见光、紫外线,易被感知、 感觉,如太阳发光、火炉发热等。 问题与思考:人体在冬季和夏季辐射是否一样? 结束 (2)一切物体都在不断的辐射着电磁波。为什 么? 进一步思考:物体在辐射的同时还有吸收! 前页 后页
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 3 3.性质 (1)物体的温度不同辐射的能量不同(电磁波 的波长不同) 。或者说. 注意:低温物体的辐射远红外线,不易觉察; 高温物体的辐射可见光、紫外线,易被感知、 感觉,如太阳发光、火炉发热等。 问题与思考:人体在冬季和夏季辐射是否一样? (2)一切物体都在不断的辐射着电磁波。为什 么? 进一步思考:物体在辐射的同时还有吸收!

量 4.热平衡辐射(thermal radiation of balance) 若物体辐射能等于它在相同时间内吸收的辐 射能时,物体的温度保持不变,此过程称为 光电 热平衡辐射。 推论:一个物体辐射能小于它同一时间内吸 收的辐射能,物体的温度将升高;否则,温 度降低。 结 注意!物体吸收和辐射不相等,但过程缓慢 短时间内有确定温度。 返回 为描述物体的热辐射引进
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 4 若物体辐射能等于它在相同时间内吸收的辐 射能时,物体的温度保持不变,此过程称为 热平衡辐射。 推论:一个物体辐射能小于它同一时间内吸 收的辐射能,物体的温度将升高;否则,温 度降低。 注意!物体吸收和辐射不相等,但过程缓慢, 短时间内有确定温度。 为描述物体的热辐射引进 4.热平衡辐射(thermal radiation of balance)

量子 5.辐出度 (radiant exitance 物体在单位时间、单位表面积上的辐射能量称为辐 出度,用MT)表示.单位为:Wm2 物体对某一单色光的辐出度称为单色辐出度M(T) 注意!) 对于波长在 入-人+d讥范围的辐出度dM,T) dM,(T)=M,(T)da 那么: 小 某一温度下物体对所有波长的总辐出度为: 作业 结束 M(T)=0aM,(T)=。M,(T1入 问题与思考:这是物体某一温度下的总辐出度。 返回 那么任意温度下的总辐出度? 前页 2010.11 10:10:1 好!物体辐射和吸收能量是物体的属性,辐射复杂
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 5 5.辐出度(radiant exitance) 物体在单位时间、单位表面积上的辐射能量称为辐 出度,用M (T)表示.单位为:W·m-2 物体对某一单色光的辐出度称为单色辐出度M λ (T) 注意!对于波长在 范围的辐出度 那么: 某一温度下物体对所有波长的总辐出度为: 好!物体辐射和吸收能量是物体的属性,辐射复杂。 dM(T) dM T T d ( )=M( ) 问题与思考:这是物体某一温度下的总辐出度。 那么任意温度下的总辐出度? λ− λ+dλ

量 力学 基础 二.黑体辐射(black body radiation) 1.黑体(black body 如果一个物体对入射的电磁波能全部吸收, 即称为黑体。黑体可以吸收投射到其表面 上所有波长的辐射能量,显然黑体是一种 光电 理想模型。 应 问题与思考: 理想模型类别,学了那些? 2.黑体模型 结束 实验室的黑体 模型!黑洞! 生活中的黑体 模型? 返回 play 9 注意:实验表明, 在一定温度下黑体的辐射能按波长分布。 后页 6
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 6 如果一个物体对入射的电磁波能全部吸收, 即称为黑体。黑体可以吸收投射到其表面 上所有波长的辐射能量,显然黑体是一种 理想模型。 二.黑体辐射(black body radiation) 1.黑体(black body ) 2.黑体模型 实验室的黑体 模型!黑洞! 生活中的黑体 模型? 注意:实验表明,在一定温度下黑体的辐射能按波长分布。 问题与思考:理想模型类别,学了那些?
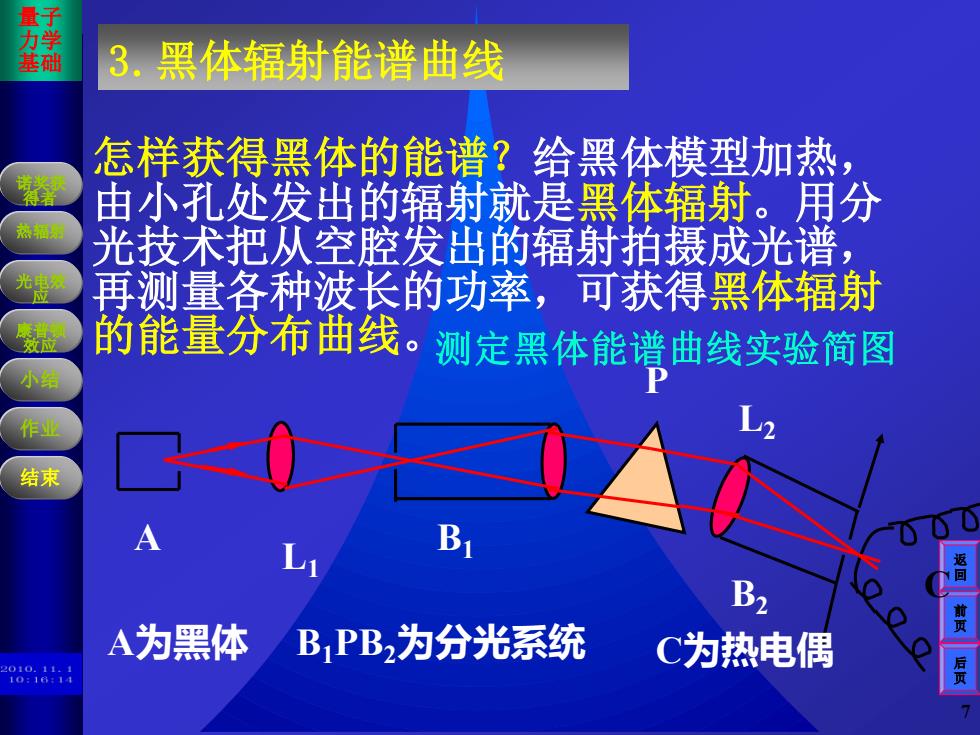
量子 3.黑体辐射能谱曲线 怎样获得黑体的能谱?给黑体模型加热, 由小孔处发出的辐射就是黑体辐射。用分 热 光技术把从空腔发出的辐射拍摄成光谱, 再测量各种波长的功率,可获得黑体辐射 的能量分布曲线。测定黑体能谱曲线实验简图 作 结束 B2 前页 A为黑体 BPB,为分光系统 C为热电偶
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 7 怎样获得黑体的能谱?给黑体模型加热, 由小孔处发出的辐射就是黑体辐射。用分 光技术把从空腔发出的辐射拍摄成光谱, 再测量各种波长的功率,可获得黑体辐射 的能量分布曲线。 3.黑体辐射能谱曲线 P L2 B2 A L1 B1 C A为黑体 B1PB2为分光系统 C为热电偶 测定黑体能谱曲线实验简图

量 力学 基础 注意看图!能否找出其中的规律? (1)温度升高,各波长的能量增加, 总辐射能量增加: 光电辣 应 (2)任意温度下,册 1700K 1500K 作 有辐射最强的波 1300K 结束 长(3)温度升高, 100K 辐射最强的波长 向短波方向移动。 返回 λ(m 注意:根据以上实验事实,可总结两个重要的黑体辐射定律
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 8 Mλ (T) 1 2 3 4 λ(μm) 1700K 1500K 1300K 1100K 注意看图!能否找出其中的规律? (2)任意温度下, 有辐射最强的波 长(3)温度升高, 辐射最强的波长 向短波方向移动。 (1)温度升高,各波长的能量增加, 总辐射能量增加. 注意:根据以上实验事实,可总结两个重要的黑体辐射定律:

量子 力学 基础 4.两个重要的定律 (1)Stefan and Boltzman Law 实验证明:总辐射能量M(T)=M,T)d,与绝 对温度T的四次方成正比,即 M(T)=oT4 光电 o=5.67×10-8w/mk4,称为斯蒂芬常数。 相关连接:斯蒂芬(J.Stefan)建立了黑体的总辐 出度与绝对温度之间关系的经验公式,制成辐射 作 高温计,测得太阳表面温度约为6000K; 结束 1884年玻尔兹曼根据经典的热力学理论证明了公 式的成立,故此定律称为斯蒂芬一玻尔兹曼定律。 启发:在已知物体表面温度时,我们可以求出物 前页 体因辐射损失的质量。太阳的辐射! 10:1:14
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 9 4.两个重要的定律 (1)Stefan and Boltzman Law 相关连接: 斯蒂芬(J.Stefan)建立了黑体的总辐 出度与绝对温度之间关系的经验公式,制成辐射 高温计,测得太阳表面温度约为6000K; 1884年玻尔兹曼根据经典的热力学理论证明了公 式的成立,故此定律称为斯蒂芬-玻尔兹曼定律。 实验证明:总辐射能量M(T)=∫Mλ (T)dλ与绝 对温度T的四次方成正比,即 M (T)=σT4 σ= 5.67×10-8 w/m2k 4 ,称为斯蒂芬常数。 启发:在已知物体表面温度时,我们可以求出物 体因辐射损失的质量。太阳的辐射!
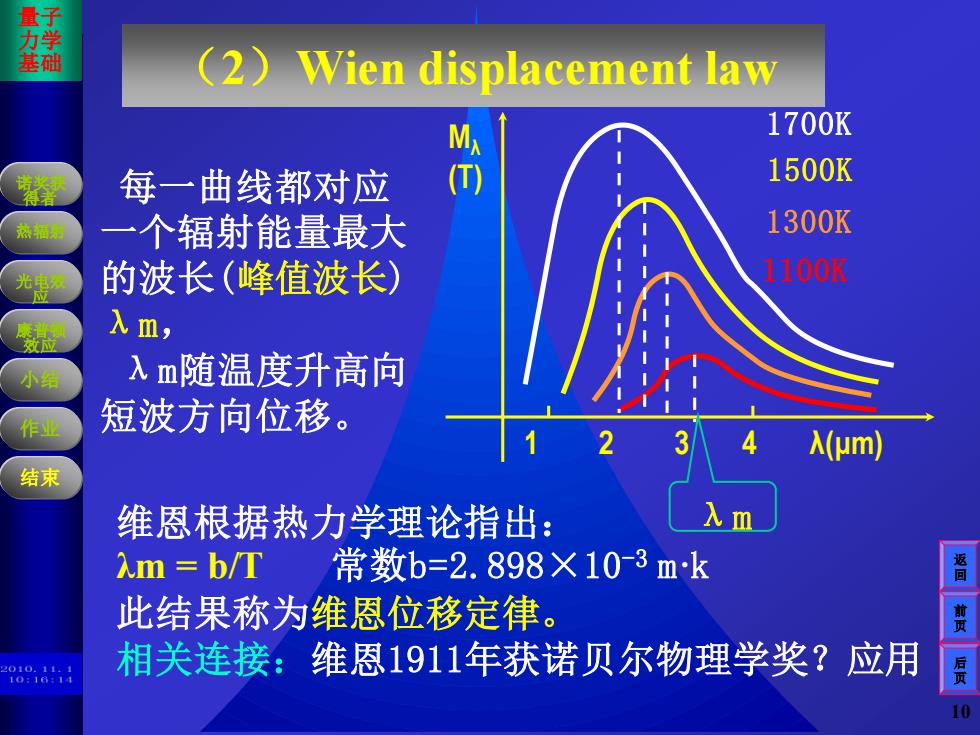
量子 力学 基础 (2)Wien displacement law 1700K 若奖用 每一曲线都对应 1500K 一个辐射能量最大 1300K 光电辣 的波长(峰值波长)》 1100K 入m, 应 小结 入m随温度升高向 作 短波方向位移。 (m) 结束 维恩根据热力学理论指出: Am b/T 常数b=2.898×10-3mk 此结果称为维恩位移定律。 相关连接:维恩1911年获诺贝尔物理学奖?应用 10
魏杰制作 ,版权所 有,不得 翻录。 魏杰制作 ,版权所 有,不得 翻录。 光电效 应 康普顿 效应 作业 诺奖获 得者 量子 力学 基础 小结 热辐射 前 页 后 页 返 回 结束 10 (2)Wien displacement law 维恩根据热力学理论指出: λm = b/T 常数b=2.898×10-3 m·k 此结果称为维恩位移定律。 相关连接:维恩1911年获诺贝尔物理学奖?应用 Mλ (T) 1 2 3 4 λ(μm) 1100K 1300K 1500K 1700K 每一曲线都对应 一个辐射能量最大 的波长(峰值波长) λm, λm随温度升高向 短波方向位移。 λm