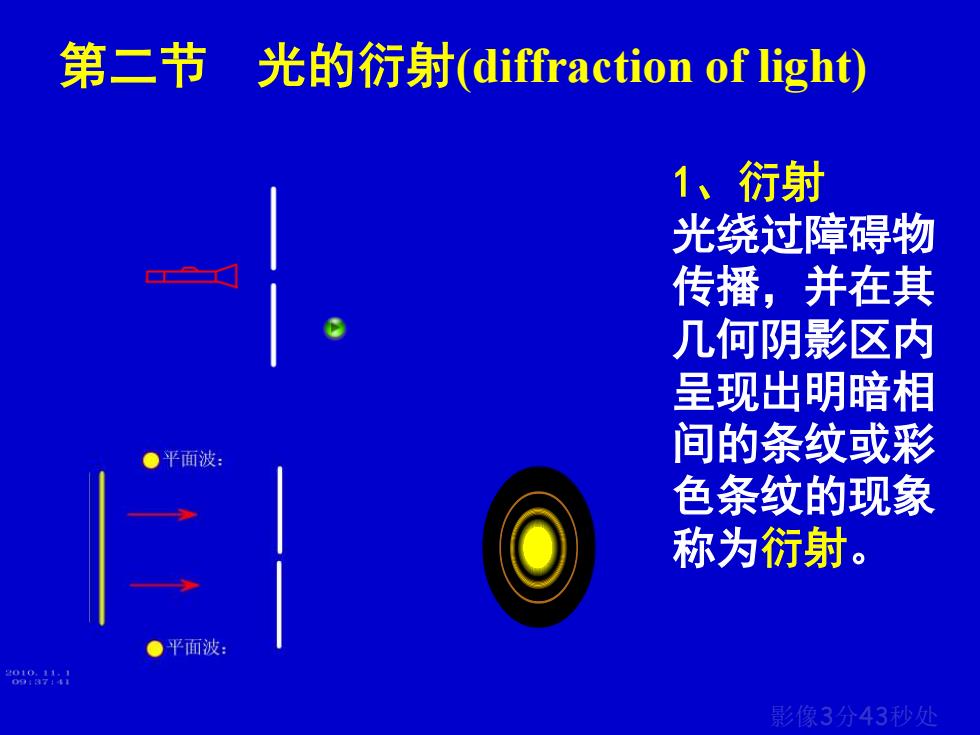
第二节光的衍射(diffraction of light) 1、衍射 光绕过障碍物 传播,并在其 几何阴影区内 呈现出明暗相 D平面波 间的条纹或彩 色条纹的现象 称为衍射。 ●平面波: 480a 影像3分43秒处
第二节 光的衍射(diffraction of light) 影像3分43秒处 1、衍射 光绕过障碍物 传播,并在其 几何阴影区内 呈现出明暗相 间的条纹或彩 色条纹的现象 称为衍射
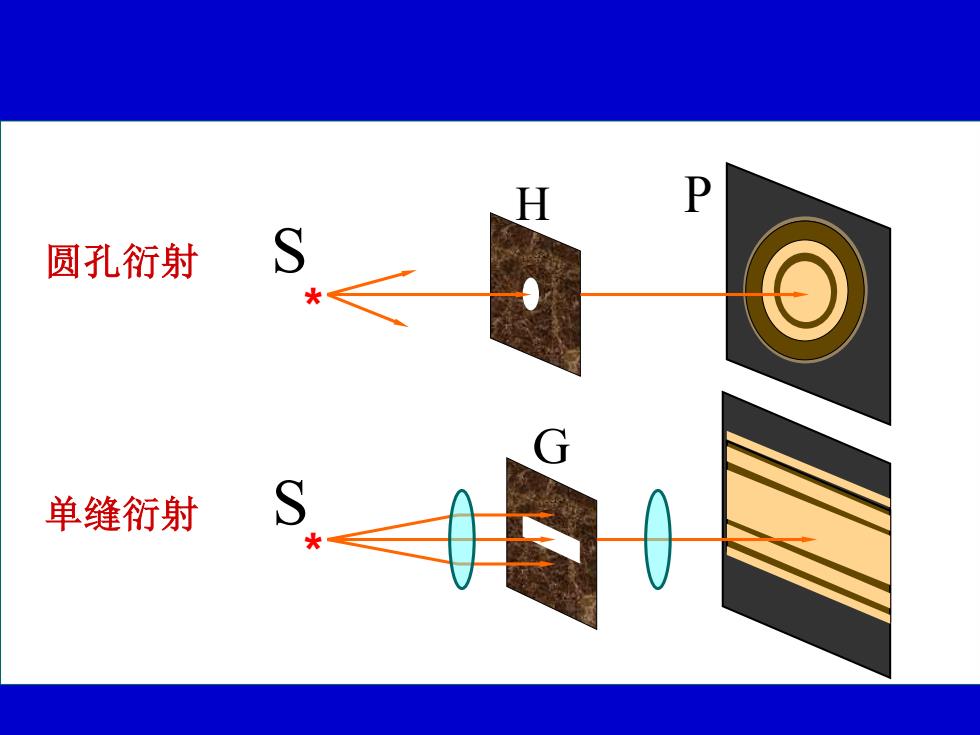
圆孔衍射 S 单缝衍射 S
圆孔衍射 单缝衍射 H P * S G * S

2、衍射产生的原因 媒质中波阵面上的每一点都是新波源,向各个方向发出子 波,子波若在传播过程中相遇,即会叠加,产生干涉。此 即惠更斯一菲涅耳原理。 波的衍射 水波通过狭缝后的衍射
波 的 衍 射 水 波 通 过 狭 缝 后 的 衍 射 媒质中波阵面上的每一点都是新波源,向各个方向发出子 波,子波若在传播过程中相遇,即会叠加,产生干涉。此 即惠更斯-菲涅耳原理。 2、衍射产生的原因
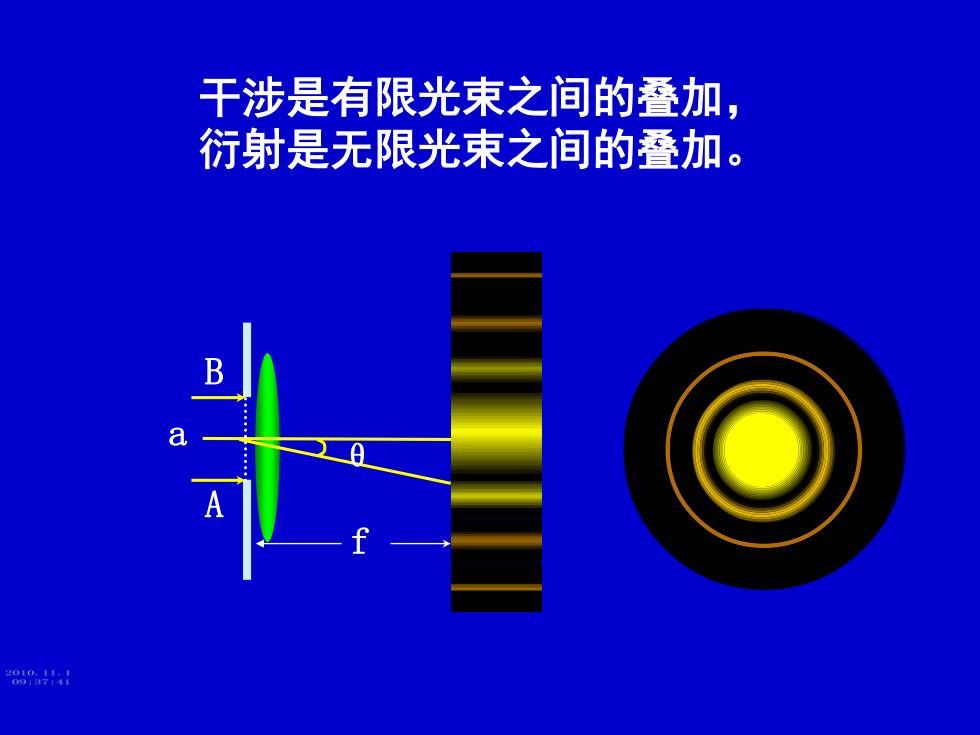
干涉是有限光束之间的叠加, 衍射是无限光束之间的叠加。 288a
A B f θ a 干涉是有限光束之间的叠加, 衍射是无限光束之间的叠加
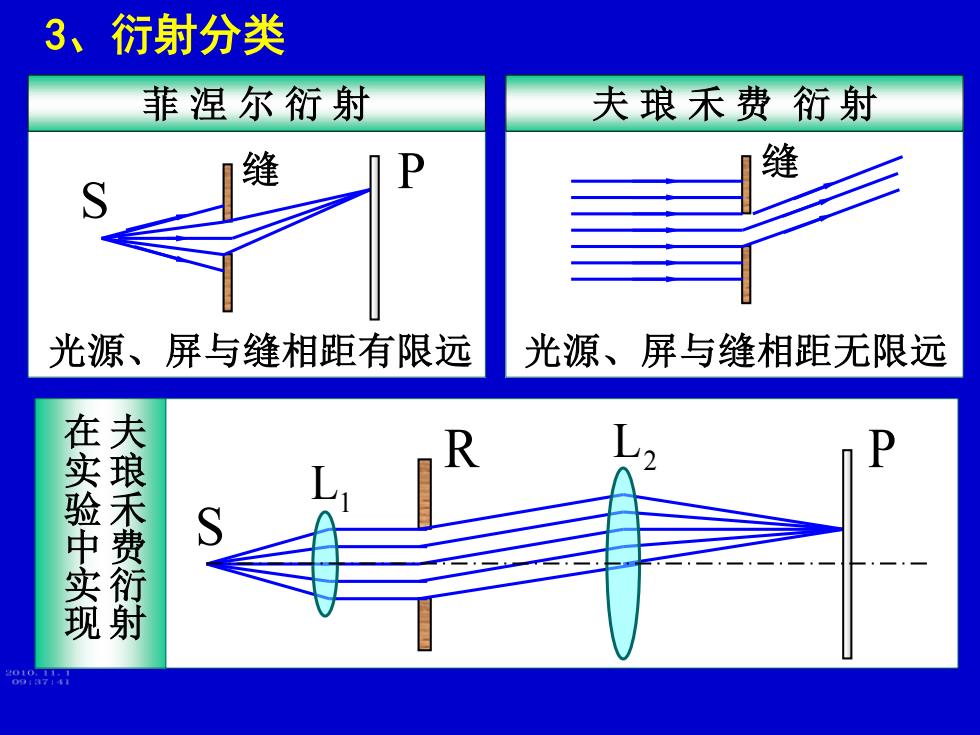
3、衍射分类 菲涅尔衍射 夫琅禾费衍射 缝 缝 光源、屏与缝相距有限远 光源、屏与缝相距无限远 8a
3、衍射分类 夫 琅 禾 费 衍 射 光源、屏与缝相距无限远 缝 L1 L2 在 实 验 中 实 现 夫 琅 禾 费 衍 射 S R P 菲 涅 尔 衍 射 缝 P S 光源、屏与缝相距有限远

一、夫琅禾费单缝衍射 B 狭逢 开始 ③返回 子波与原入射光之间的夹角日称为衍射角。 0371 问题:衍射角日为多大值出现暗纹或明纹?
一、夫琅禾费单缝衍射 子波与原入射光之间的夹角θ称为衍射角。 问题:衍射角θ为多大值出现暗纹或明纹?
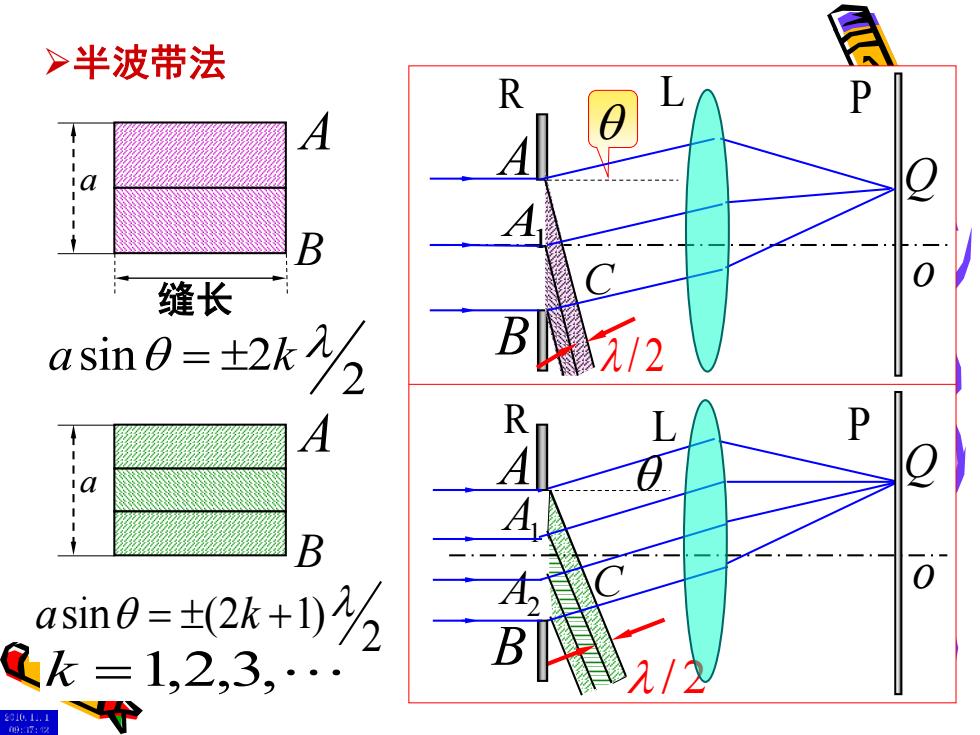
>半波带法 P A 缝长 asin0=±2k3 B 元/2 D A R 'a A asin8=±(2k+0)2 0 0k=1,2,3, /
o R P A B Q sin 2 2 a k = sin (2 1) 2 a k = + ➢半波带法 k =1,2,3, A1 A2 C / 2 a A B a 缝长 A B o A Q B R L P C A1 / 2 L
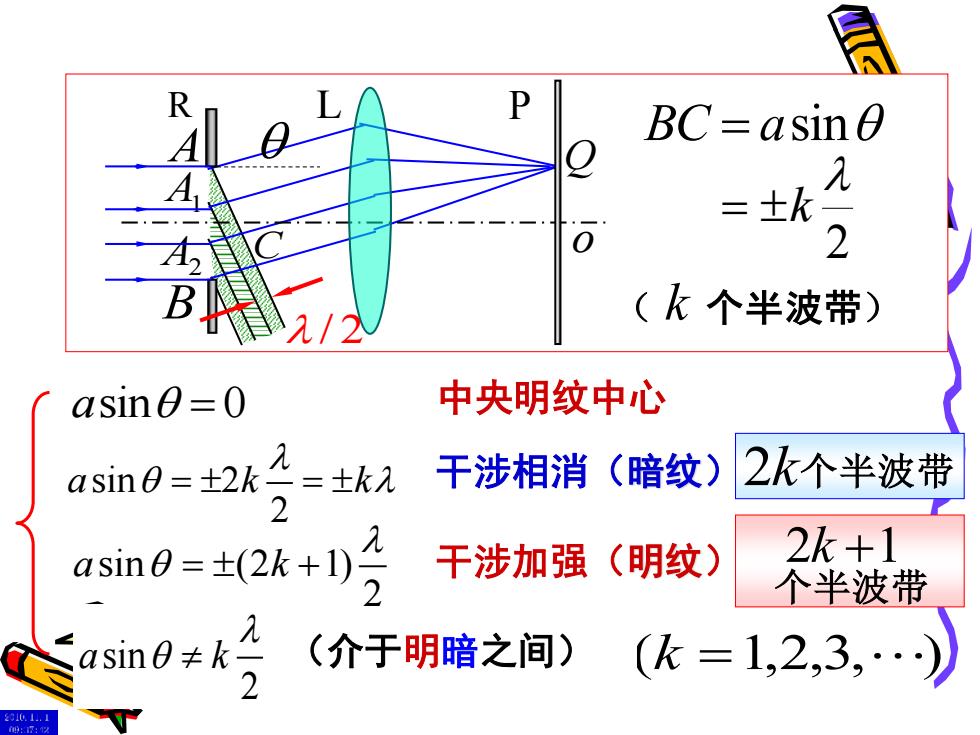
P BC=asin = 士k 0 2 (飞个半波带) asin=0 中央明纹中心 asin0=±2k =±k入 干涉相消(暗纹) 2k个半波带 2 snB=(2k+1片 干涉加强(明纹) 2k+1 个半波带 asin0≠k (介于明暗之间) (k=1,2,3,》 2
(k =1,2,3, ) sin 2 2 a k k = = 干涉相消(暗纹) sin (2 1) 2 a k = + 干涉加强(明纹) sin 2 a k (介于明暗之间) L o R P A Q B A1 A2 C / 2 BC a = sin 2 = k ( k 个半波带) 2k 个半波带 个半波带 2k +1 asin 0 = 中央明纹中心
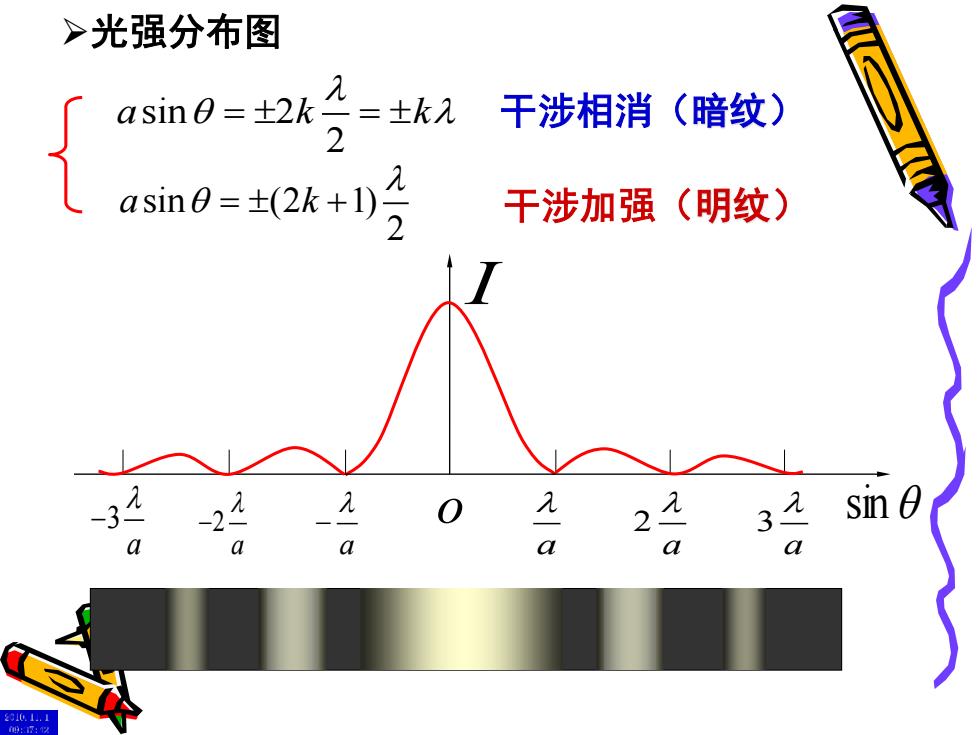
>光强分布图 2=士k元 干涉相消(暗纹) asin0=±(2k+)2 干涉加强(明纹) 2 3 ¥Snθ a a a
sin I o a 2 a 3 a a 2 − a 3 − a − sin (2 1) 2 a k = + 干涉加强(明纹) sin 2 2 a k k = = 干涉相消(暗纹) ➢光强分布图
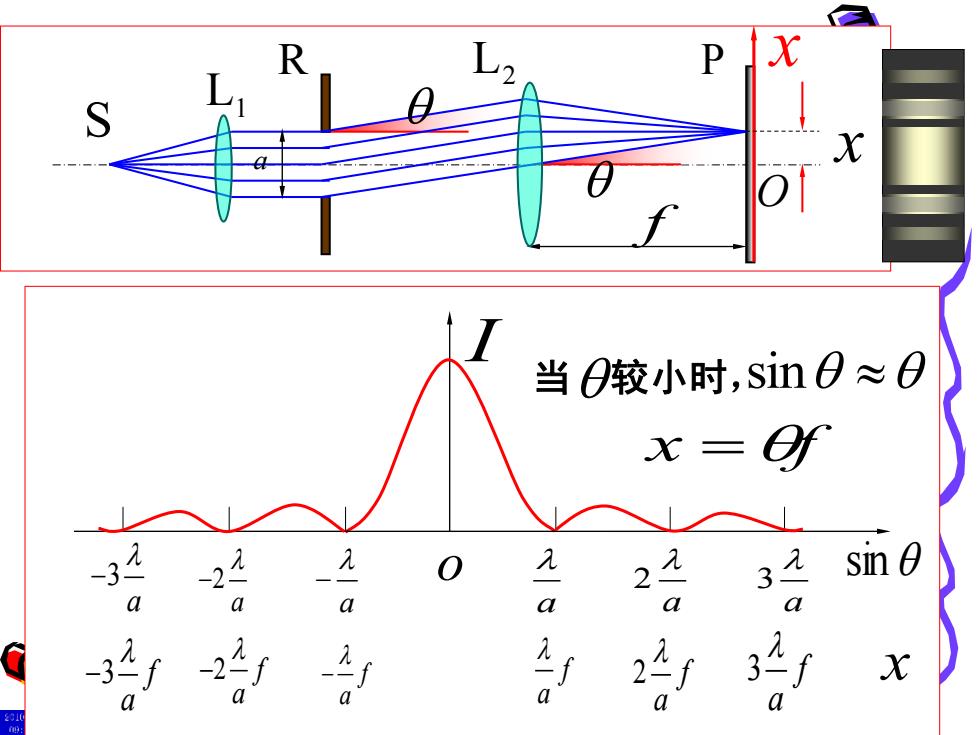
当O较小时,sin0≈0 2 3 元 si 0 a a a 34 X
L1 L2 f a S R P O x x sin x =f 当 较小时, f x a f a − 2 f a 2 f a 3 f − a − 3 f a sin I o a 2 a 3 a a 2 − a 3 − a −