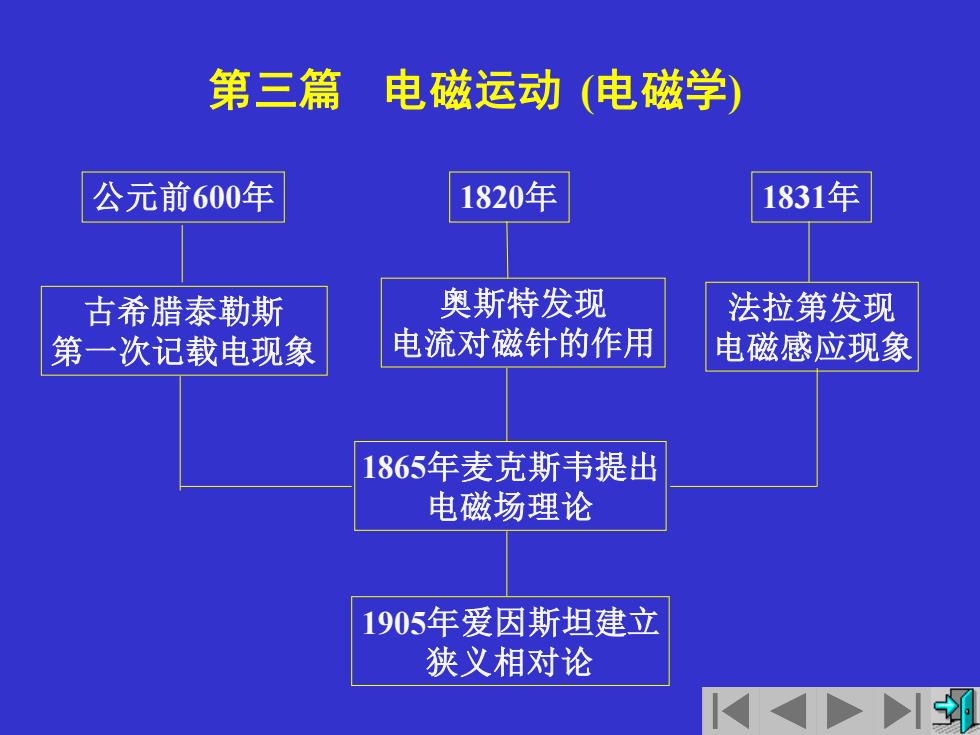
第三篇 电磁运动(电磁学) 公元前600年 1820年 1831年 古希腊泰勒斯 奥斯特发现 法拉第发现 第一次记载电现象 电流对磁针的作用 电磁感应现象 1865年麦克斯韦提出 电磁场理论 1905年爱因斯坦建立 狭义相对论
1905年爱因斯坦建立 狭义相对论 1865年麦克斯韦提出 电磁场理论 1820年 奥斯特发现 电流对磁针的作用 公元前600年 1831年 法拉第发现 电磁感应现象 古希腊泰勒斯 第一次记载电现象 第三篇 电磁运动 (电磁学)

第九章 静电场 静电场-一一相对于观察者静止的电荷产生的电场 ●两个物理量: 场强、电势 ● 一个实验规律:库仑定律 ●两个定理: 高斯定理、环流定理 9-1电荷库仑定律 ☆自然界中只存在正、负两种电荷 一电荷 ☆电荷守恒定律:在一个孤立系统内发生的 过程中,正负电荷的代数和保持不变。 ☆电荷的量子化效应:Q=Ne
第九章 静电场 静电场-相对于观察者静止的电荷产生的电场 ● 两个物理量: 场强、电势 ● 一个实验规律:库仑定律 ● 两个定理: 高斯定理、环流定理 9-1 电荷 库仑定律 ☆自然界中只存在正、负两种电荷 ☆电荷守恒定律: 在一个孤立系统内发生的 过程 中,正负电荷的代数和保持不变。 ☆电荷的量子化效应:Q=Ne 一.电荷

二.库仑定律(静电场的基本实验规律) 1定律内容:F=K92元。 2 定律的一般形式: 令 K三 4π60 则真空中: F- 4927f 2 4元E0r 无限大介质中: 9192 士之4元EE≥ 91 ●2
2 0 1 2 r r q q F K = 2 0 0 1 2 4 r r q q F = 2 0 0 1 2 4 r r q q F r = 二.库仑定律(静电场的基本实验规律) 1.定律内容: 4 0 1 令 K = 则真空中: 无限大介质中: r 0 r • q2 • q1 r r r 0 = 定律的一般形式:
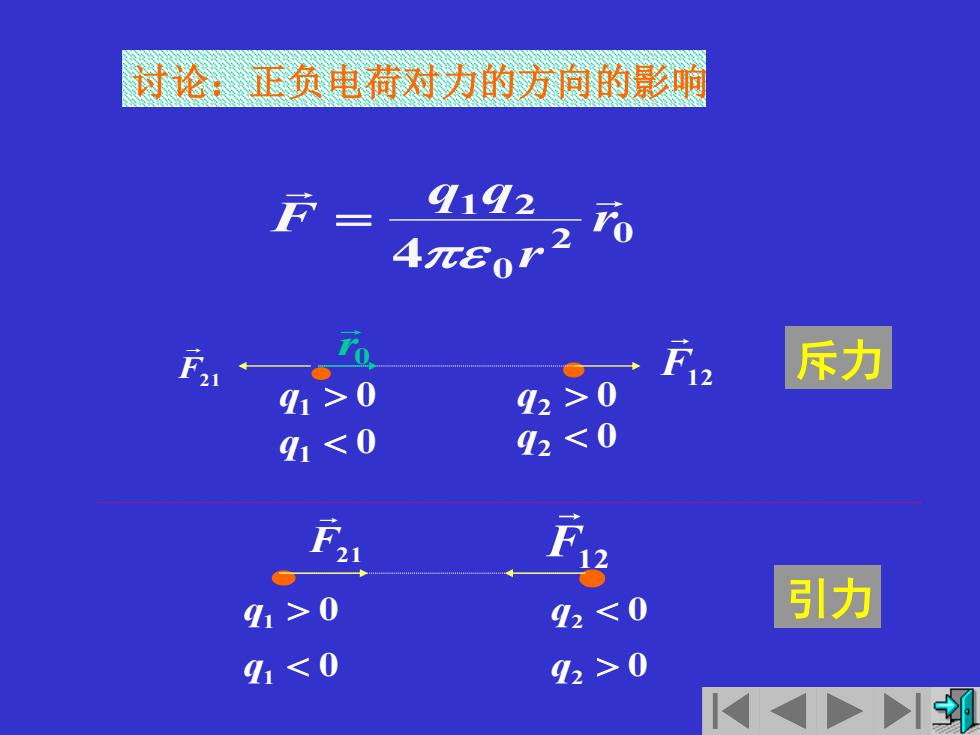
讨时论:正负电荷对力的方向的影响 9192 4πe0r2 斥力 91>0 93>0 91≤0 920 92≤0 引力 9q1≤0 92>0
• • q1 0 q2 0 q1 0 q2 0 F12 F21 0 r 2 0 0 1 2 4 r r q q F = 讨论:正负电荷对力的方向的影响 • • q1 0 q1 0 q2 0 q2 0 F12 F21 斥力 引力
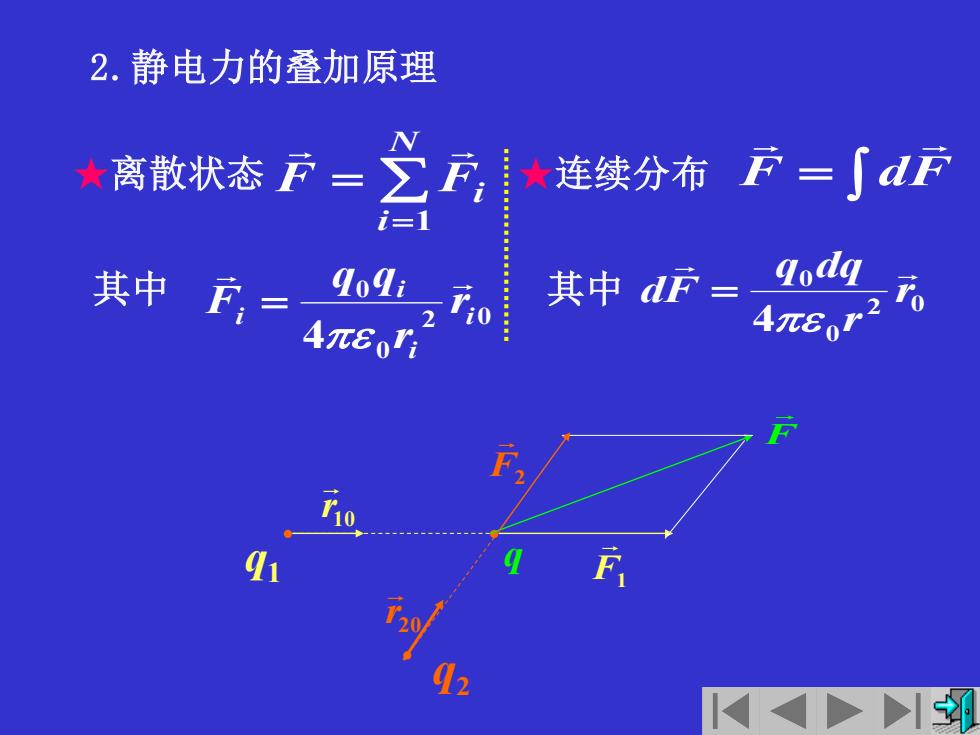
2.静电力的叠加原理 ★离散状态下=】 ★ 连续分布F=∫d下 中= 共中=2
q1 q2 q 2.静电力的叠加原理 ★离散状态 = = N i F Fi 1 其中 2 0 0 0 4 i i i i r r q q F = ★连续分布 F = dF 2 0 0 0 4 r r q dq dF 其中 = 10 r F1 F F2 20 r

例12-1氢原子在氢原子中,电子与质子的距离 为5.3x101米,试求静电引力及万有引力,并比 较这两个力的数量关系。 解:由于电子与质子之间距离约为它们自身直 径的10倍,因而可将电子、质子看成点电荷
5 10 解:由于电子与质子之间距离约为它们自身直 径的 倍,因而可将电子、质子看成点电荷。 例 12-1 氢原子 在氢原子中,电子与质子的距离 11 5.3 10− 为 米,试求静电引力及万有引力,并比 较这两个力的数量关系

·电子与质子之间静电力(库仑力)为吸引力 数量为FE=e2/46R2=8.2×10-8m ·电子与质子之间的万有引力为 F。=GmM/R2=3.6×10-47N ·所以库仑力与万有引力数值之比为 FE/Fc=2.3×1039 考虑带电粒子间的相互作用力时,可忽略万有引力
●所以库仑力与万有引力数值之比为 3 9 FE FG = 2.310 考虑带电粒子间的相互作用力时, 可忽略万有引力。 2 8 0 2 4 8 2 10− FE = e R = . ●电子与质子之间的万有引力为 数量为 2 47 3 6 10− FG = GmM R = . (N) ●电子与质子之间静电力(库仑力)为吸引力 (N)
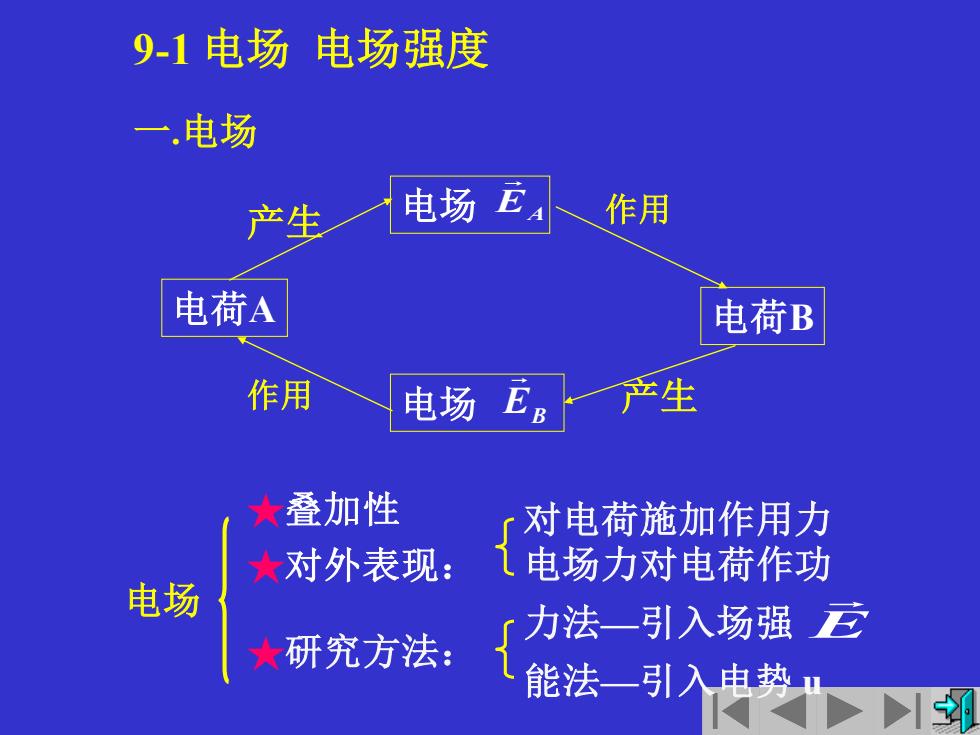
9-1电场电场强度 一电场 产生 电场卫 作用 电荷A 电荷B 作用 电场 E 产生 ★ 叠加性 「对电荷施加作用力 ★对外表现: 电场力对电荷作功 电场 ★研究方法: ∫力法一引入场强五 能法一引入电势
力法—引入场强 一.电场 电场 EA 电场 EB 电荷A 电荷B 产生 产生 作用 作用 电场 ★叠加性 ★对外表现: 能法—引入电势 u E 对电荷施加作用力 电场力对电荷作功 9-1 电场 电场强度 ★研究方法:

二,电场强度一描述电场的基本物理量 ★试验电荷q。:电荷量足够小的点电荷 比例系数与试验电荷电量无关 1定义:它= 电场中某点的电场强度在数值和方向上等于单位 正电荷在该点所受的电场力。单位:NC-1‖v/m
F 1.定义: q0 F E = ★试验电荷 q0 :电荷量足够小的点电荷 电场中某点的电场强度在数值和方向上等于单位 正电荷在该点所受的电场力。单位: Q 0 q A q0 B q0 C 二.电场强度—描述电场的基本物理量 NC v m −1 0 F q 比例系数与试验电荷电量无关

注意 a.空间是否存在场以及电场的强弱和方向, 与试验电荷q0无关,而由场本身决定。 b.在电场中,空间每一点都相应有一个 矢量 E为点函数,记作E(x,y,z》
注意 b.在电场中,空间每一点都相应有一个 与试验电荷 q0 无关,而由场本身决定。 a.空间是否存在场以及电场的强弱和方向, E 矢量 E E( x, y,z ) 为点函数,记作