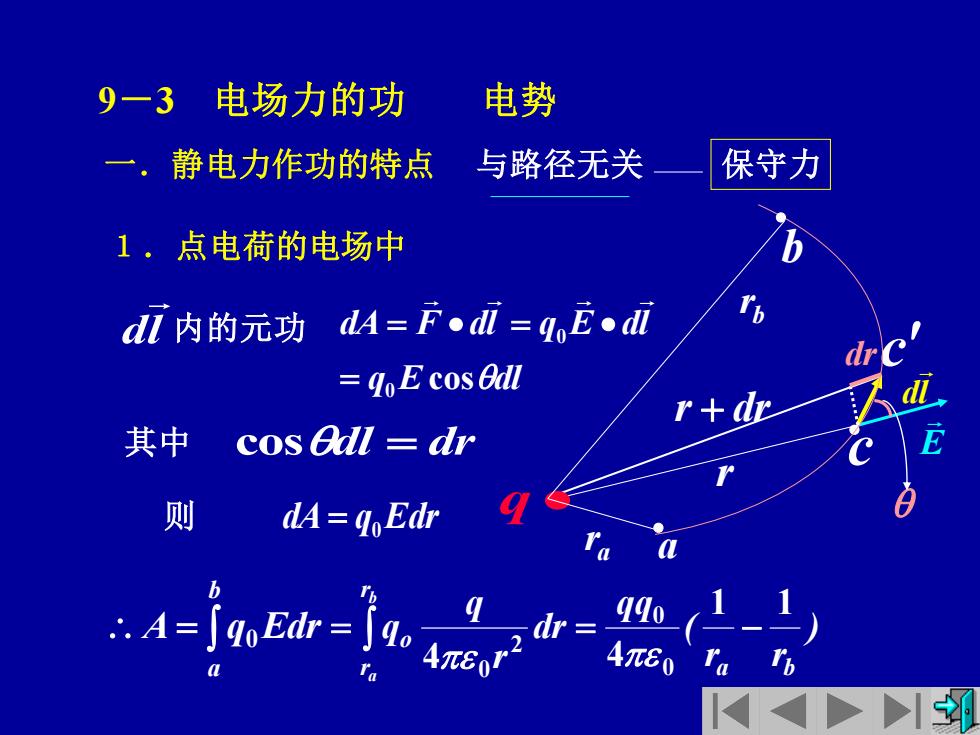
9一3电场力的功 电势 一.静电力作功的特点 与路径无关 保守力 1。点电荷的电场中 di内的元功dA=F●dl=,E●dl go E cos Odl r dt 其中cos adl=dr 则 dA=q Edr
r r + dr c dl c E b a 9-3 电场力的功 电势 1.点电荷的电场中 保守力 q E dl dA F dl q E dl 0 cos 0 = = • = • dl 内的元功 其中 cosdl = dr = b a A q Edr 0 dA q Edr 则 = 0 与路径无关 q • a r b r dr 一.静电力作功的特点 = = − b a r r a b o ) r r ( qq dr r q q 1 1 4 4 0 0 2 0

2,点电荷系的电场中 (与路径无关) Ab=o(E1+E2+.+En)l jga+jg.ea+jgEm 4+++4 460 Tia Tib
2.点电荷系的电场中 = + + + • b a a b n A q ( E E E ) dl 0 1 2 = • + • + • b a b a b a q E dl q E dl q E dl 0 1 0 0 = + + + = − i i a i b i n ) r r ( q q A A A 1 1 4 0 0 1 2 (与路径无关)

二.静电场的环流定理(做功与路径无关的数学表达式) qo沿闭合路径abeda一周电场力所作的功 Ab=fqoEd=∫gE·l+∫qE●l acb bda =∫qEl-∫qE●i=0 adb 即静电场力移动电荷沿任一闭和路径所作的功为零。 .q0≠0 ,·静电场中电场强度立的环流恒为零 fE。du=0
= • = • + • acb bda a b A q E dl q E dl q E dl 0 0 0 = • − • = acb adb q E dl q E dl 0 0 0 二.静电场的环流定理(做功与路径无关的数学表达式) a c b d 即静电场力移动电荷沿任一闭和路径所作的功为零。 q0 0 静电场中电场强度 E 的环流恒为零 E • dl = 0 q0 沿闭合路径 abcda 一周电场力所作的功

三.电势能 重力(保守力)的功=重力势能增量的负值 所以静电力的功=静电势能增量的负值 a点电势能W 试验电荷q处于 b点电势能W, 则a一b电场力的功4b=o∫Ei=W。-W 取 W。=0 W。=Am=jqE。l ★注意:W。属于q及 E系统
重力(保守力)的功=重力势能增量的负值 所以 静电力的功=静电势能增量的负值 b点电势能 Wb 则 a b 电场力的功 = • b a ab A q E dl 0 Wa Wb = − 取 = 0 W = = • a a a W A q E dl 0 ★注意: Wa q0 E 系统 属于 及 试验电荷 q0 处于 a点电势能 Wa a b 三.电势能

四.电势电势差 W。=ja,Ed 1,电势u定义u。= Wa E●d 0 单位正电荷在该点所具有的电势能 单位正电荷从该点到无穷远点电场力所作的功 2电势差4。-4,电场中任意两点的电势之差(电压) 4b=4。-4,=∫Eod-了Edl -fEdi-jEcoson 单位正电荷从a一→ 电场力的功
四.电势 电势差 1.电势 u = = • a a a E dl q W u 0 单位正电荷在该点所具有的电势能 单位正电荷从该点到无穷远点电场力所作的功 2.电势差 ua − ub 电场中任意两点的电势之差(电压) = − = • − • a b ab a b u u u E dl E dl = • = b a b a E dl Ecosdl 单位正电荷从a b 电场力的功 = • a a W q E dl 0 定义

五.电势叠加原理 若场源为q1q2。·。·Im的点电荷系 根据电场叠加原理场中任一点的 场强 E=E1+E2+.+En 电势 =El=E+E,+.+ed %+h++.=4 各点电荷单独存在时在该点电势的代数和
根据电场叠加原理场中任一点的 五.电势叠加原理 若场源为 q1 q2qn 的点电荷系 场强 电势 En E E E . = 1 + 2 + + = • = • + • + + • P P n P P u E dl E dl E dl E dl . 1 2 = = + + + = n i u u un ui 1 1 2 . 各点电荷单独存在时在该点电势的代数和

六.电势的计算 1.点电荷电场中的电势 如图P点的场强为卫= 4e,r 肉电势定义0-E-品 4π61 ①大小q>0>0rfu↓r+o"=0(最小) 兼讨论 q<0<0rfu↑root=0(最大) ②对称性以q为球心的同一球面上的点电势相等
1.点电荷电场中的电势 六.电势的计算 r q • • P 0 r 如图 P点的场强为 2 0 4 0 r r q E = = • = = P r P r q dr r q u E dl 0 2 0 4 4 由电势定义得 讨论 ② 对称性 ① 大小 q>0 u>0 r u r u = 0 (最小) q<0 u<0 r u r u = 0 (最大) 以q为球心的同一球面上的点电势相等

2.点电荷系的电势 由电势叠加原理,P的电势为 u=zw=2 3.连续带电体的电势 由电势叠加原理 dq =血-
由电势叠加原理,P的电势为 2.点电荷系的电势 = = i i i r q u u 4 0 = = r dq u du 4 0 3.连续带电体的电势 由电势叠加原理 dq • P r r1 • q1 q2 • n • q 2 P r n r

例1.求电偶极子电场中任一点P的电势 由叠加原理 up=%+42= 9=43-r) P(x,y) 4πr1 4π6'2 4π2 .r>>lr2-1≈lcos 9≈r2 q Icose .= 4π6 其中2=x2+y2 cos0 1 px 4π€0
例1.求电偶极子电场中任一点P的电势 l − q O + q X Y r 1 r 2 r P(x, y) • 0 1 2 2 1 0 1 0 2 1 2 4 ( ) 4 4 r r q r r r q r q uP u u − = + = − = 由叠加原理 r l r2 − r1 l cos 2 1 2 r r r 2 0 cos 4 r q l u = 2 2 2 r = x + y 2 2 cos x y x + 其中 = 2 3 0 2 2 ( ) 4 1 x y px u + =

课堂练习:已知正方形顶点有四个等量的电点荷4.0x10’C r=5cm ①求u。 4=491=28.8×102Y 4π8,r 94 ②将q=1.0x10’c从0一0 电场力所作的功 A0=4o(4。-4)=qo(0-28.8×102)=-28.8×10-7J ③求该过程中电势能的改变 A∞0=W。-W=-28.8×102<0 电势能
V r q u 2 0 1 28.8 10 4 = 4 = r O 1 q2 q q4 q3 课堂练习:已知正方形顶点有四个等量的电点荷 r=5cm C 9 4.0 10− ①求 ②将 ③求该过程中电势能的改变 uo q c 9 0 1.0 10− = 从 0 电场力所作的功 A q u u q J 2 7 0 0 ( 0 ) 0 (0 28.8 10 ) 28.8 10− = − = − = − 28.8 10 0 2 A0 = W −W0 = − 电势能