
置高斯定滋
93电通量电场中的高斯定理 一。 电力线(电场的图示法) 方向:切线 性质: 不闭合 大小:E= AN 电力线密度 不相交; AS 起于正、止于负
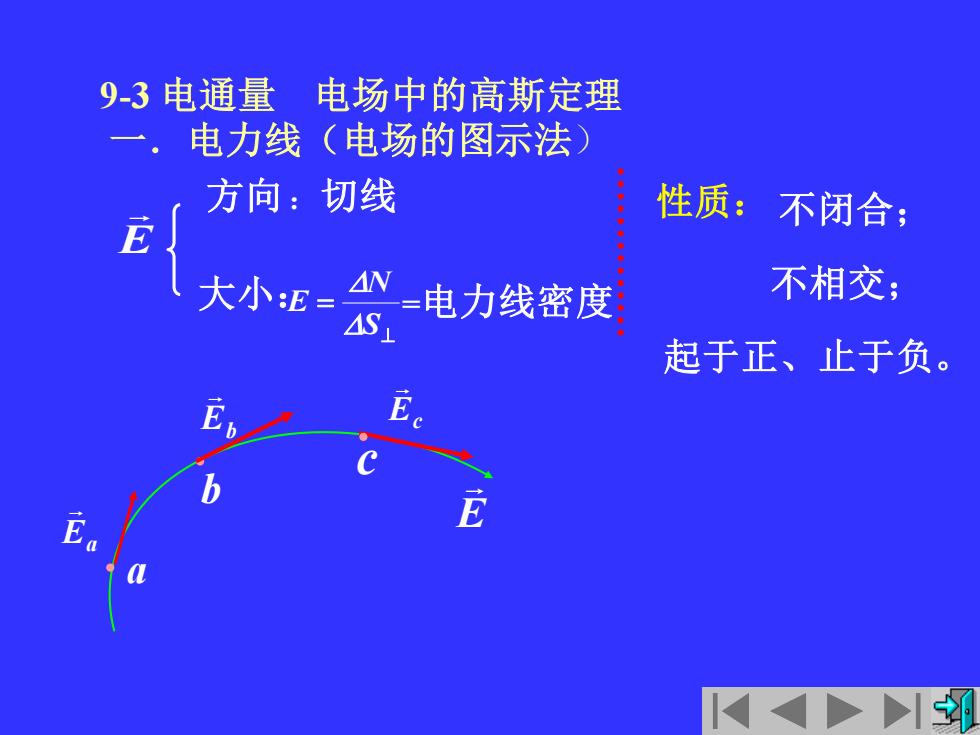
E Ec 9-3 电通量 电场中的高斯定理 一.电力线(电场的图示法) ⊥ = S N E 大小: E 方向:切线 =电力线密度 性质: b c Ea Eb a 不相交; 不闭合; 起于正、止于负
二.电通量Φ,(电场强度通量通过任一面的电力线数 Φ,=ES Φ=E●S=ESc0s0 E DE=∫E●瓜=∫Eds cos0 Φ。=fE●瓜=∮Ecos 0
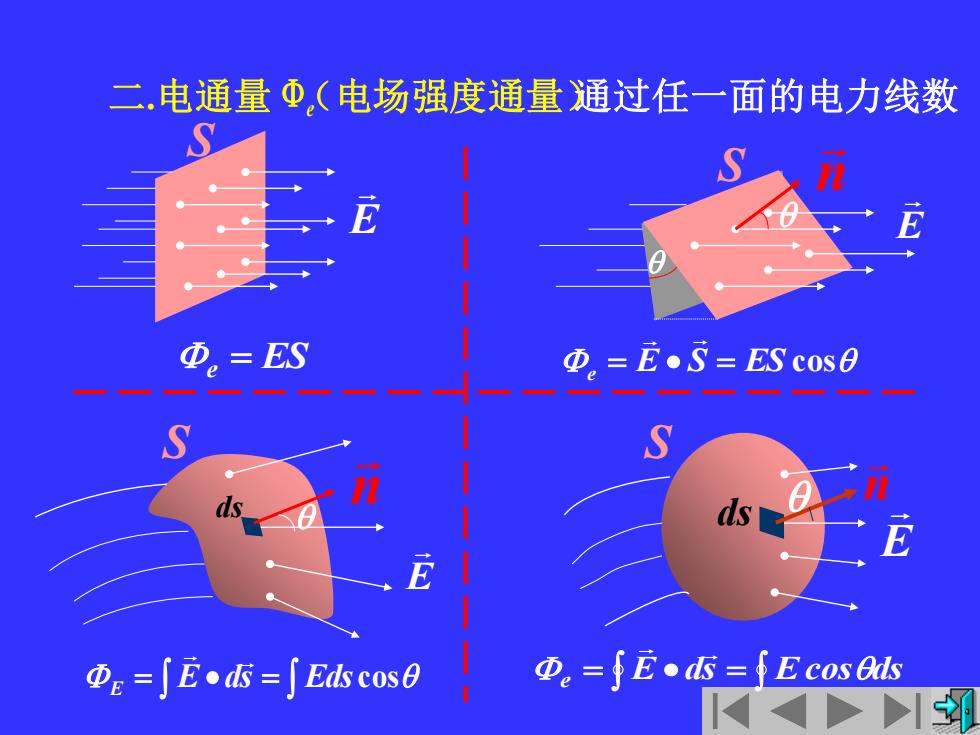
S E S 二.电通量 (电场强度通量) e 通过任一面的电力线数 e = ES E = E • ds = Eds cos e = E • S = ES cos = E • ds = Ecos ds e S E n E n ds S E ds n

例5.计算均匀电场中一圆柱面的电通量。己知E及R 解:。=手E本=∫E●+∫E本+∫E。 S1 S2 33 =∫Ecos180°+∫Ecos90°k+∫Ecos0°k S1 =-E元R2+0+元R2E =0 S2 R
S1 ds n 解: 例5.计算均匀电场中一圆柱面的电通量。已知 E 及 R = • = • + • + • 1 2 3 s s s e E ds E ds E ds E ds = + + 1 2 3 0 0 0 180 90 0 s s s E cos E cos ds E cos ds E R R E 2 2 = − + 0+ = 0 E R S3 ds n n S2

1.求均匀电场中一半球面的电通量。 课堂练习 2.在均匀电场E=3i+2j中,过Y0Z平面内 面积为S的电通量。 X Φ=E。S Ds,+Ds2 =0 =(3i+2j)●Si Ds,+(-EπR2)=0 =3S Ds,=E元R2
1. 求均匀电场中一半球面的电通量。 2. 在均匀电场 E i j = 3 + 2 中,过YOZ平面内 面积为S的电通量。 课 堂 练 习 E R O n n n n S1 S2 0 1 2 S + S = 0 2 1 S + ( −ER ) = 2 1 S = ER E S = • ( i j ) Si = 3 + 2 • = 3S X O Y Z S E n

93电通量 场中的高斯定理 一电力线 二电通量 三.高斯定理: d3 92 通过任意闭合曲面的电通量(E通量) 等于这个闭合 曲面所包围的电荷的代数和除以。而与闭合曲面外 的电荷无关。 真空中 .=E=∑
9-3 电通量 场中的高斯定理 三.高斯定理: 一.电力线 二.电通量 E 通过任意闭合曲面的电通量( 通量 ) 等于这个闭合 0 曲面所包围的电荷的代数和除以 而与闭合曲面外 的电荷无关。 = • = i s e E ds q 0 1 真空中 q1 q3 q2 S
1.q位于球面S的球心 ⊕ Φ,=∫E函=∫Ecos0°公 -faa ds d 2.q位于任意曲面S'内 Φ,=中,= 60
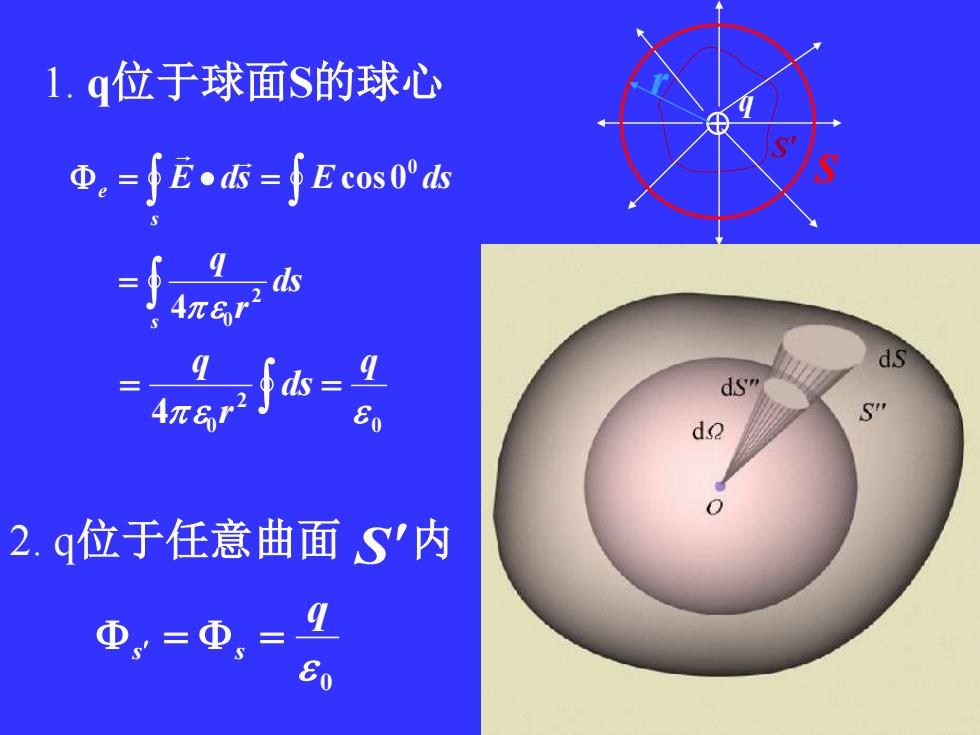
= = • = s s e ds r q E ds E ds 2 0 0 4 cos0 = = 0 2 4 0 q ds r q 1. q位于球面S的球心 2. q位于任意曲面 S 内 0 q s = s = S q S r

3.q位于任意闭合曲面4.曲面内包围多个点电荷 S”以外 ①e=∫E西 =fE1+E2+.+En) =E●瓜+5E+.+∫En●西 =+2+.+n 0 60 ·2
3. q位于任意闭合曲面 S 以外 s = 0 4. 曲面内包围多个点电荷 = E • ds e = ( E + E + .+ E )• ds n 1 2 = E • ds + E • ds + .+ E • ds n 1 2 0 0 2 0 1 n q q q = + ++ = i q 0 1 q S S q1 n q q2

注意: ★过曲面的通量由曲面内的电荷决定 ★高斯面上的场强E是由全部电荷(面内外电荷)共同产生 ★对连续带电体,高斯定理为 ★无限大均匀介质中 ∫E。本= 1 ∑4 四.高斯定理的应用 当场源分布具有高度对称性时求场强分布 步骤:1.对称性分析,确定E的大小、方向分布特征 2.作高斯面,计算电通量及∑4 3.利用高斯定理求解
注意: ★过曲面的通量由曲面内的电荷决定 ★高斯面上的场强 E 是由全部电荷(面内外电荷)共同产生 ★对连续带电体,高斯定理为 E • ds = dq 0 1 ★无限大均匀介质中 • = i r E ds q 0 1 当场源分布具有高度对称性时求场强分布 步骤:1.对称性分析,确定 E 的大小、方向分布特征 2.作高斯面,计算电通量及 qi 3.利用高斯定理求解 四.高斯定理的应用

9-3电通量 场中的高斯定理 一.电力线 二.电通量 三高斯定理: 更,-fE=∑4 四.高斯定理的应用 当场源分布具有高度对称性时求场强分布 步骤:1,对称性分析,确定E的大小、方向分布特征 2.作高斯面,计算电通量及∑4 3利用高斯定理求解
当场源分布具有高度对称性时求场强分布 步骤:1.对称性分析,确定 E 的大小、方向分布特征 2.作高斯面,计算电通量及 qi 3.利用高斯定理求解 四.高斯定理的应用 9-3 电通量 场中的高斯定理 三.高斯定理: 一.电力线 二.电通量 = • = i s e E ds q 0 1