
第四章从经典物理学到量子力学 §4-1从经典物理学到前期量子论 到19世纪末,经典物理学已经建立了比 较完整的理论体系。 力学 分析力学,存在海王星的 预言及其被证实 电磁学 麦克氢原子光谱斯韦方程 组,预言了电磁波的存在 热力学+统计物理学 量子力学的研究对象:微观粒子
第四章 从经典物理学到量子力学 §4 - 1 从经典物理学到前期量子论 到 19 世纪末,经典物理学已经建立了比 较完整的理论体系。 力学 分析力学,存在海王星的 预言及其被证实 电磁学 麦克氢原子光谱斯韦方程 组,预言了电磁波的存在 热力学+统计物理学 量子力学的研究对象:微观粒子

量子理论的发展轨迹: 能量子:黑体辐射 光量子:光电效应 固体比热 氢原子光谱 黑体辐射普朗克的能量子假说 (1)热辐射的基本概念 热辐射:一切物体的分子热运动将导致物 体向外不断地发射电磁波。这种辐射与温度 有关。温度越高,发射的能量越大,发射的 电磁波的波长越短。 614
614 量子理论的发展轨迹: 能量子:黑体辐射 光量子:光电效应 固体比热 氢原子光谱 一 黑体辐射 普朗克的能量子假说 ( 1 ) 热辐射的基本概念 热辐射:一切物体的分子热运动将导致物 体向外不断地发射电磁波。这种辐射与温度 有关。温度越高,发射的能量越大,发射的 电磁波的波长越短

平衡热辐射或平衡辐射:如果物体辐射出 去的能量恰好等于在同一时间内所吸收的 能量,则辐射过程达到了平衡。 单色辐射出射度(简称单色辐出度,用 M2(T表示):在单位时间内从物体表面单位 面积上所辐射出来的,单位波长范围内的电 磁波能量,即 Mi(T)=dM(T) (4. d 1) where dM(T):在单位时间内从物体表 面单位面积上所辐射出来的,波长在入到 615
615 平衡热辐射或平衡辐射:如果物体辐射出 去的能量恰好等于在同一时间内所吸收的 能量,则辐射过程达到了平衡。 单色辐射出射度(简称单色辐出度,用 M (T) 表示):在单位时间内从物体表面单位 面积上所辐射出来的,单位波长范围内的电 磁波能量,即 d d ( ) ( ) M T M T = , (4. 1) where dM ( T ):在单位时间内从物体表 面单位面积上所辐射出来的,波长在 到

λ+d入范围内的电磁波能量。 辐射出射度(简称辐出度,在单位时间内 从物体表面单位面积上辐射出来的各种波 长电磁波能量的总和) M(T)=∫dMT)=0M(T)dn. (4. 2) 单色吸收比a(2,T)和单色反射比p元,T):在 温度为T时,物体吸收和反射波长在1到2 +d九范围内的电磁波能量,与相应波长的 入射电磁波能量之比,分别称为该物体的单 616
616 +d 范围内的电磁波能量。 辐射出射度(简称辐出度,在单位时间内 从物体表面单位面积上辐射出来的各种波 长电磁波能量的总和) = = 0 M (T) dM(T) M (T)d . (4. 2) 单色吸收比 (,T) 和单色反射比 (,T) :在 温度为 T 时,物体吸收和反射波长在 到 + d 范围内的电磁波能量,与相应波长的 入射电磁波能量之比,分别称为该物体的单

色吸收比(2,T和单色反射比p2,T。对于不 透明的物体,有 a(2,T)+p(2,T)=1. (4.3) (2)基尔霍夫定律和黑体 基尔霍夫辐射定律:对每一个物体来说, 单色辐出度与单色吸收比的比值 M2(I1a(,),是一个与物体性质无关(而只与 温度和辐射波长有关)的普适函数。即 M1(-M22(O=.=1元,T), (4.4) a1(2,T)a2(2,T) 1(,T)=?引出黑体的概念
617 色吸收比 (,T) 和单色反射比 (,T) 。对于不 透明的物体,有 (,T) + (,T) = 1. (4. 3) ( 2 ) 基尔霍夫定律和黑体 基尔霍夫辐射定律: 对每一个物体来说, 单色辐出度与单色吸收比的比值 M (T)/(,T) ,是一个与物体性质无关(而只与 温度和辐射波长有关)的普适函数。即 ( , ) ( , ) ( ) ( , ) ( ) 2 2 1 1 I T T M T T M T = == , (4. 4) I T ( , ) ? = 引出黑体的概念

推论:如果一个物体是良好的吸收体,必 定也是一个良好的辐射体。 绝对黑体(简称黑体):如果物体在任何 温度下,对于任何波长的入射辐射能的吸收 比都等于1,即0(2,T)=1。黑体既是最好的吸收体,又是 最好的辐射体 对黑体,基尔霍夫辐射定律(用Moa(①是黑体的 单色辐出度) MiT)=MoiT). (4. o(,T) 5) 与 M,)_M2①==1,T刀 41(,TD2(,T) 618
618 推论:如果一个物体是良好的吸收体,必 定也是一个良好的辐射体。 绝对黑体(简称黑体):如果物体在任何 温度下,对于任何波长的入射辐射能的吸收 比都等于 1,即 ( , ) 0 T = 1。黑体既是最好的吸收体,又是 最好的辐射体。 对黑体,基尔霍夫辐射定律(用 ( ) M0 T 是黑体的 单色辐出度) ( ) ( , ) ( ) M T T M T = . (4. 5) 与 ( , ) ( , ) ( ) ( , ) ( ) 2 2 1 1 I T T M T T M T = ==

比较可见 M(T=I(,T), 黑体单色辐出度M(I是研究热辐射的一个 中心问题。 自然界中的物体都 不是绝对黑体。即使物 体表面熏了煤烟最多 也只能吸收98%左右 的入射电磁波能量。 图4-1带有小孔的空腔 绝对黑体的模型:用不透明材料如金属制成一个空心容器 器壁上开一个很小的孔O如果小孔0的面积远小于容器内表面的面积,那么反射次数 N就会很大,这意味着射入空腔小孔O的电磁波能量几乎全部被吸收,吸收比近似为 1.空腔中的电磁辐射常称为黑体辐射。 619
619 比较可见 ( ) ( , ) M0 T = I T , 黑体单色辐出度 ( ) M0 T 是研究热辐射的一个 中心问题。 自然界中的物体都 不是绝对黑体。即使物 体表面熏了煤烟,最多 也只能吸收 98 %左右 的入射电磁波能量。 绝对黑体的模型:用不透明材料(例如金属)制成一个空心容器, 器壁上开一个很小的孔 O.如果小孔 O 的面积远小于容器内表面的面积,那么反射次数 N 就会很大,这意味着射入空腔小孔 O 的电磁波能量几乎全部被吸收,吸收比近似为 1.空腔中的电磁辐射常称为黑体辐射。 图4 - 1 带有小孔的空腔

在常温下所有物体的辐射都很弱,由于黑色物体或空腔小孔的反射又极少,故看 起来它们很暗;然而在高温下,由于黑体的辐射最强,故看起来它们最明亮。 (3)黑体辐射的基本规律 斯特藩-一玻耳兹曼定律:黑体的辐射出射 度与黑体绝对温度的四次方成正比(来自实验和理 论)】 Mo(T)=oT4 (4.6) 斯特藩常量 o=5.67051×108W.m-2.K-4 维恩位移律(从热力学理论号出,黑体辐射光道中辐射最强的波长m 与黑体温度T之间满足关系)) AT=b
620 在常温下所有物体的辐射都很弱,由于黑色物体或空腔小孔的反射又极少,故看 起来它们很暗;然而在高温下,由于黑体的辐射最强,故看起来它们最明亮。 ( 3 ) 黑体辐射的基本规律 斯特藩−玻耳兹曼定律:黑体的辐射出射 度与黑体绝对温度的四次方成正比(来自实验和理 论) 4 0 M (T) = T , (4. 6) 斯特藩常量 = 5. 670 51 10−8 W m−2 K −4. 维恩位移律(从热力学理论导出,黑体辐射光谱中辐射最强的波长m 与黑体温度 T 之间满足关系) mT =b

(4.7) 常量为 b=2.897756×10-3m.K
621 (4. 7) 常量为 b = 2. 897 756 10−3 m K
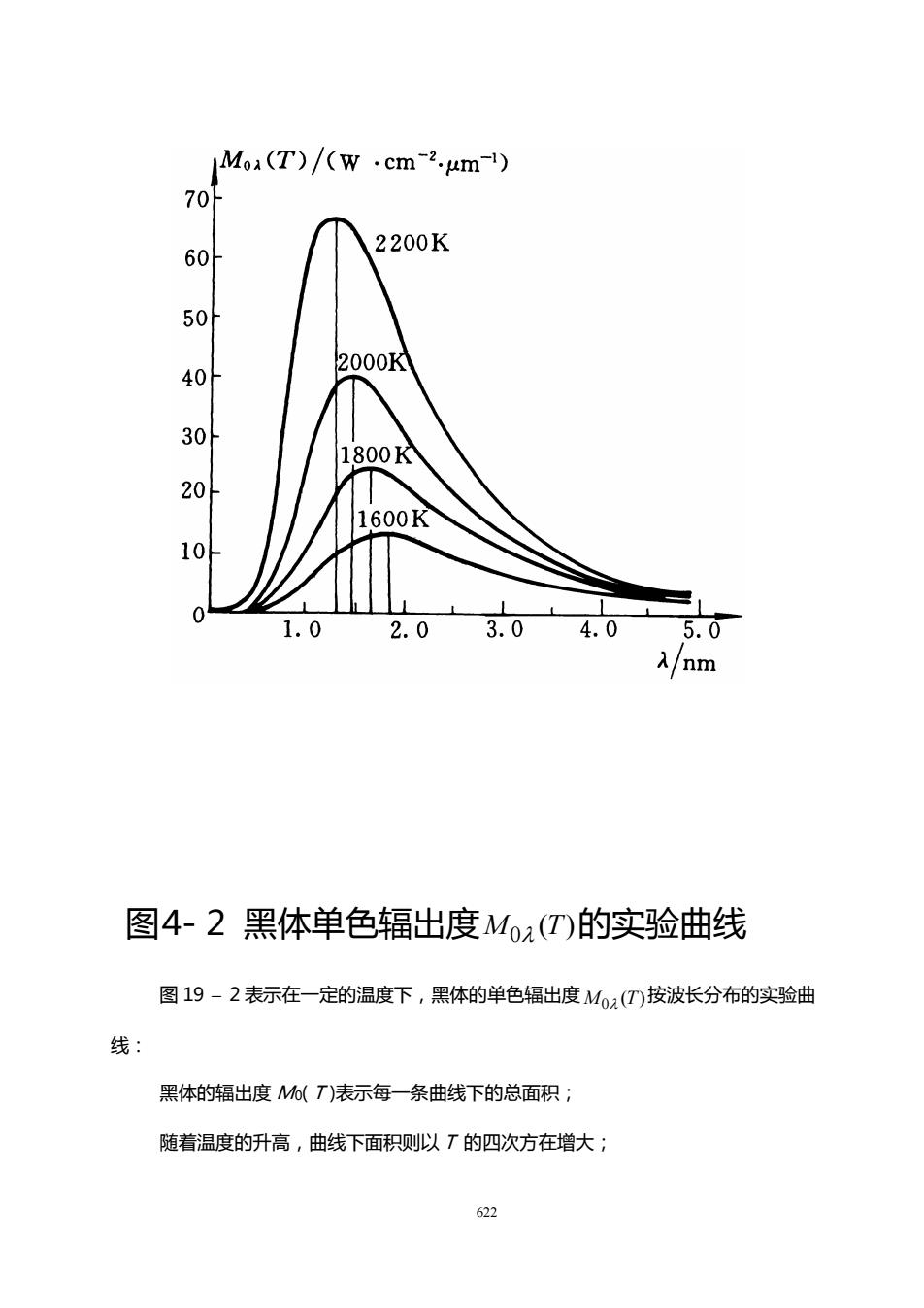
Moa(T)/(w·cm-2.um) 70 2200K 60 50 2000K 40 30 1800K 20H 600 10 nm 图4-2黑体单色辐出度Moa(T)的实验曲线 图19-2表示在一定的温度下,黑体的单色辐出度M0()按波长分布的实验曲 线: 黑体的辐出度M%(T)表示每一条曲线下的总面积 随着温度的升高,曲线下面积侧以T的四次方在增大;
622 图 19 – 2 表示在一定的温度下,黑体的单色辐出度 ( ) M0 T 按波长分布的实验曲 线: 黑体的辐出度 M0( T )表示每一条曲线下的总面积; 随着温度的升高,曲线下面积则以 T 的四次方在增大; 图4- 2 黑体单色辐出度 ( ) M0 T 的实验曲线