
Review 。正旋电磁场 ·正旋电磁场的复数表示 ● 麦克斯韦方程组的复数形式 ● 复介质参数 。复坡印亭矢量 ●复坡印亭定理 ●时变电磁场的唯一性定理 lexu@mail.xidian.edu.cn
Review 正旋电磁场 正旋电磁场的复数表示 麦克斯韦方程组的复数形式 复介质参数 复坡印亭矢量 复坡印亭定理 时变电磁场的唯一性定理 lexu@mail.xidian.edu.cn 2 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review 电场强度矢量的复数表示 E(x,y,=,t)=Rel(E+aE+a.E)e] =Reld+Em+aEm)e] Rel] E(x,y,=,t) j0E(x,y,2) 复(振幅)矢量 81 Ex,y2,①←Ex,y2=a它m+a,立,m+a.立m lexu@mail.xidi 四维函数←一马三维函数
Review 电场强度矢量的复数表示 lexu@mail.xidian.edu.cn 3 ( , , , ) Re[( ˆˆˆ ) ] Re[ ˆˆˆ ) ] Re[ ] x y z j j j j t x xm y ym z zm j t x xm y ym z zm j t Exyzt aE e aE e aE e e aE aE aE e Ee φ φ φ ω ω ω = ++ = ++ = 复(振幅)矢量 (, , ,) (, , ) ˆˆˆ Exyzt Exyz aE aE aE ↔ =++ x xm y ym z zm 四维函数←→三维函数 (, , ,) (, ,) Exyzt j Exyz t ω ∂ ↔ ∂ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review 。复数形式的麦克斯韦方程组 VxH(r)=J(r)+j@D(r) V×E()=土joB(的 V.B(r)=0 V.D(r)=p 。复数形式的电流连续性方程 VxJ=-jop lexu@mail.xidian.edu.cn
Review 复数形式的麦克斯韦方程组 复数形式的电流连续性方程 lexu@mail.xidian.edu.cn 4 ∇× = + Hr Jr j Dr () () () ω ∇× = − Er j Br () () ω ∇⋅ = B r() 0 ∇⋅ = D r( ) ρ ∇× = − J jωρ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review 介电常数及磁导率的虚 ·复介质参数 部反映介质的损耗,且 与损耗功率成正比 极化 介电常数(电容率) 8。=6'(0)-j8"(o) 磁化 磁导率 电磁场 4。='(0)-ju"(0 轰 传导 电导率 G.=0'(0)-jo"(⊙ 静态场 6.-8-18a 实常数 lexu@mail.xidian.edu.cn 5 等效复介电常数
Review 复介质参数 lexu@mail.xidian.edu.cn 5 极化 磁化 传导 介电常数(电容率) 磁导率 电导率 实常数 静态场 时变电磁场 '( ) "( ) c ε εω ε ω = − j '( ) "( ) c σ σω σ ω = − j '( ) "( ) c µω ω = − u ju 正数 介电常数及磁导率的虚 部反映介质的损耗,且 与损耗功率成正比 " " tan , tan ' ' ε µ ε µ δ δ ε µ = = +−= ω σ ' j εεε " c 等效复介电常数 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

Review S()d RexRelS] Wav.e =二Re[E·D*] -Re[B.* ReJ.E*] 4 Wav.m 2 -V.S=-V ExH* =2EJ*+2@ B.*-E.D* 4 4 -ds dv j2 =Jr(Pw.c+Pav.e+Pa.m)dV+j20Wawm-Wave)dV
Review lexu@mail.xidian.edu.cn 6 0 1 1 ( ) Re * Re[ ] 2 T av S S t dt E H S T = = ×= ∫ , 1 Re[ *] 4 w BH av m = ⋅ , 1 Re[ *] 4 w ED av e = ⋅ 1 Re[ *] 2 av p JE = ⋅ 1 1 11 * *2 * * 2 2 44 S E H EJ j BH ED ω −∇ ⋅ = −∇ ⋅ × = ⋅ + ⋅ − ⋅ 2 2 2 2 2 ,,, , , 1 * 2 11 1 1 1 " " 2'' 22 2 4 4 ( ) 2( ) S V V av c av e av m av m av e V V E H dS E E H dV j H E dV p p p dV j w w dV σ ωε ωµ ω µ ε ω − ×⋅ = ++ + − = ++ + − ∫ ∫ ∫ ∫ ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

●●● 第18讲时变电磁场(v) 。波动方程 ·时变电磁场的位函数 ·时变电磁场小结 ERSITY XIDIAN.EDU.C lexu@mail.xidian.edu.cn
第18讲 时变电磁场(ⅴ) 波动方程 时变电磁场的位函数 时变电磁场小结 lexu@mail.xidian.edu.cn 7 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

时变电磁场的位函数 ·非齐次矢量波动方程 。回顾有源区域的麦克斯韦方程: 7× 又x aD V2H-us a2月 V×i=j+ =-V×J 8t aB 7×E= V2E-us o"E aJ vp 8t = V.B=0 非齐次矢量波动方程 7.D=p ● 根据场源分布及变化可以由非齐次矢量波动方程求解空 ®©简的分布,但是很多情况下,该方程很难求解
时变电磁场的位函数 非齐次矢量波动方程 回顾有源区域的麦克斯韦方程: 根据场源分布及变化可以由非齐次矢量波动方程求解空 间场的分布,但是很多情况下,该方程很难求解。 lexu@mail.xidian.edu.cn 8 D H J t ∂ ∇× = + ∂ B E t ∂ ∇× = − ∂ ∇⋅ = B 0 ∇⋅ = D ρ ∇ × ∇ × 2 2 2 H H J t µε ∂ ∇ − = −∇ × ∂ 2 2 2 E J E t t ρ µε µ ε ∂ ∂∇ ∇− = + ∂ ∂ 非齐次矢量波动方程 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

波动方程 ·电磁波的存在是麦克斯韦方程组的一个重要结果,1865年, 麦克斯韦从他的方程组推导出波动方程,并得到电磁波波 速的一般表示式,预言了电磁波的存在及电磁波与光波的 同一性 麦克斯韦第一方程和第二方程说明: 。变化的电场激发磁场,变化的磁场激发电场 一旦交变的场源在空间激发起电磁场,由于电场和磁场 的相互激发,即使场源消失,电磁场仍可独立地存在, 并由近及远地向外传播,从而形成电磁波 。任何波动都满足一个共同的规律一波动方程。 lexu@mail.xidian.edu.cn
波动方程 电磁波的存在是麦克斯韦方程组的一个重要结果,1865年, 麦克斯韦从他的方程组推导出波动方程,并得到电磁波波 速的一般表示式,预言了电磁波的存在及电磁波与光波的 同一性 麦克斯韦第一方程和第二方程说明: 变化的电场激发磁场,变化的磁场激发电场 一旦交变的场源在空间激发起电磁场,由于电场和磁场 的相互激发,即使场源消失,电磁场仍可独立地存在, 并由近及远地向外传播,从而形成电磁波 任何波动都满足一个共同的规律——波动方程。 lexu@mail.xidian.edu.cn 9 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
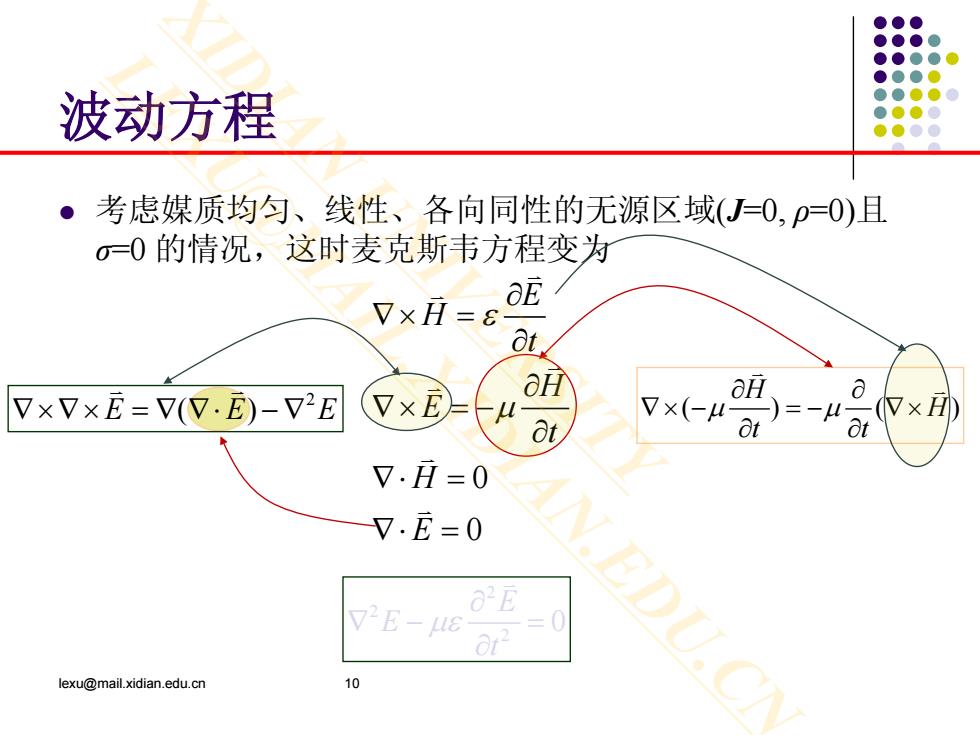
波动方程 ·考虑媒质均匀、线性、各向同性的无源区域(J=O,p=O)且 σ=0的情况,这时麦克斯韦方程变为 vx月= OE aH VxVxE=V(V.E)-V2E aH Nx(-μat =-μa (N×) 7.H=0 7.E=0 V2E-6 Or- lexu@mail.xidian.edu.cn 10
波动方程 考虑媒质均匀、线性、各向同性的无源区域(J=0, ρ=0)且 σ=0 的情况,这时麦克斯韦方程变为 lexu@mail.xidian.edu.cn 10 0 0 E H t H E t H E ε µ ∂ ∇× = ∂ ∂ ∇× = − ∂ ∇⋅ = ∇⋅ = ( ) () H H t t µ µ ∂ ∂ ∇× − = − ∇× ∂ ∂ 2 ∇×∇× =∇ ∇⋅ −∇ E EE ( ) 2 2 2 0 E E t µε ∂ ∇− = ∂ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

波动方程 V2E-Ls =0 。同理可得 VH-ue 2月 =0 812 。无源无耗区域的瞬时值矢量齐次波动方程 ·求解方法有两种: ·直接求解矢量方程 ·将矢量方程分解为标量方程求解 ●直角坐标系下的标量波动方程 ·只有在直角坐标系下,每个 a-E =0 标量方程才能只含一个未知 函数,其它正交曲线坐标系 O-B 中矢量波动方程得到的标量 ou®man波动方程都有复杂的形式。 2E82E E =0
波动方程 同理可得 无源无耗区域的瞬时值矢量齐次波动方程 求解方法有两种: 直接求解矢量方程 将矢量方程分解为标量方程求解 直角坐标系下的标量波动方程 只有在直角坐标系下,每个 标量方程才能只含一个未知 函数,其它正交曲线坐标系 中矢量波动方程得到的标量 lexu@mail.xidian.edu.cn 波动方程都有复杂的形式。 11 2 2 2 0 H H t µε ∂ ∇− = ∂ 2 2 2 0 E E t µε ∂ ∇− = ∂ 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = ∂ ∂ − ∂ ∂ + ∂ ∂ + ∂ ∂ = ∂ ∂ − ∂ ∂ + ∂ ∂ + ∂ ∂ = ∂ ∂ − ∂ ∂ + ∂ ∂ + ∂ ∂ t E z E y E x E t E z E y E x E t E z E y E x E z z z z y y y y x x x x µε µε µε XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN