西安电子科技大学：《电磁场与电磁波基础》课程教学课件（讲义，2018）第3讲 静电场（I）

电磁场与电磁波基础 主讲：徐乐 商婴子销技比是

电磁场与电磁波基础 主讲：徐乐

电磁场与电磁波绪论 ·电磁场理论的地位和作用 一是一门重要的专业基础课 ·通过电磁场和电磁波传递信息是现在以及将来通信 的一种主要手段，因此必须掌握其基本规律； ·是进一步学习一些后续课程的基础： 一电磁场理论的研究与科学技术的发展息息相关 ·很多发现和发明都是以电磁场理论的研究为基础： 指南针、电话、电报、电动机、发电机. lexu@mail.xidian.edu.cn 2

电磁场与电磁波绪论 • 电磁场理论的地位和作用 – 是一门重要的专业基础课 • 通过电磁场和电磁波传递信息是现在以及将来通信 的一种主要手段，因此必须掌握其基本规律； • 是进一步学习一些后续课程的基础； – 电磁场理论的研究与科学技术的发展息息相关 • 很多发现和发明都是以电磁场理论的研究为基础； 指南针、电话、电报、电动机、发电机…… lexu@mail.xidian.edu.cn 2

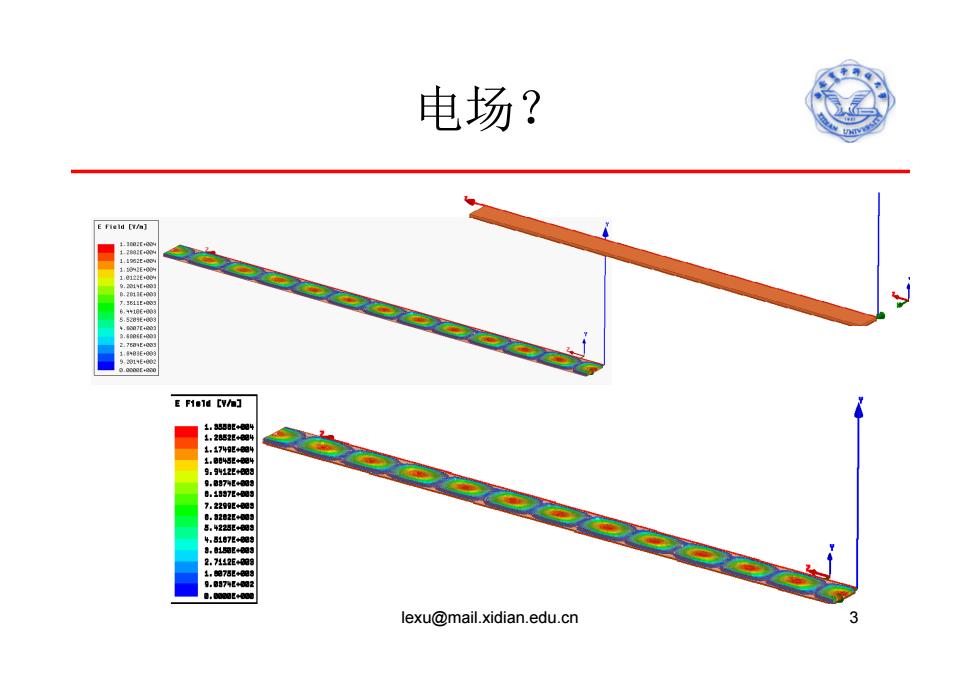
电场？ E Field [v/n] 1.1749 9412州 2.7142E40 lexu@mail.xidian.edu.cn

电场？ lexu@mail.xidian.edu.cn 3

第3讲静电场() ·真空中的场 -库仑定律 -通量与散度 -环量与旋度 ·介质中的场 -电偶极子 lexu@mail.xidian.edu.cn 4

第3讲 静电场（I） • 真空中的场 –库仑定律 –通量与散度 –环量与旋度 • 介质中的场 –电偶极子 lexu@mail.xidian.edu.cn 4

静电场 ·Why? f) -） 9 4π6F- pr）=4πEr-rl ·How? Vu V.A V×A lexu@mail.xidian.edu.cn 5

静电场 • Why? • How? lexu@mail.xidian.edu.cn 5     3 0 4 r r q r r E r              4 ' ( ) 0 r r q r      A  u   A

静电场 静电场是指相对于观察者而言静止的电荷所产生的场。 -人们对静电现象认识可追溯到两千多年前，早在 公元前585年，希腊哲学家泰勒斯(Thales)就 记载了用木块摩擦过的琥珀可以吸引细小的物体。 - 对静电场系统性、科学性研究开始于1785年法国 科学家库仑(Chavles Augustin Coulomb,1736~ 1806)发现了以其名字命名的“库仑定律”。 库仑定律和迭加原理一起，构成了静电场的理论 基础。 这节课将从库仑定律和迭加原理出发，得出描述真空中 静电场的基本方程，进而讨论介质中的静电场，静电场 的基本解法以及静电场的能量。 lexu@mail.xidian.edu.cn 6

静电场 • 静电场是指相对于观察者而言静止的电荷所产生的场。 –人们对静电现象认识可追溯到两千多年前，早在 公元前585年，希腊哲学家泰勒斯（Thales）就 记载了用木块摩擦过的琥珀可以吸引细小的物体。 –对静电场系统性、科学性研究开始于1785年法国 科学家库仑（Chavles Augustin Coulomb，1736～ 1806）发现了以其名字命名的“库仑定律”。 –库仑定律和迭加原理一起，构成了静电场的理论 基础。 • 这节课将从库仑定律和迭加原理出发，得出描述真空中 静电场的基本方程，进而讨论介质中的静电场，静电场 的基本解法以及静电场的能量。 lexu@mail.xidian.edu.cn 6

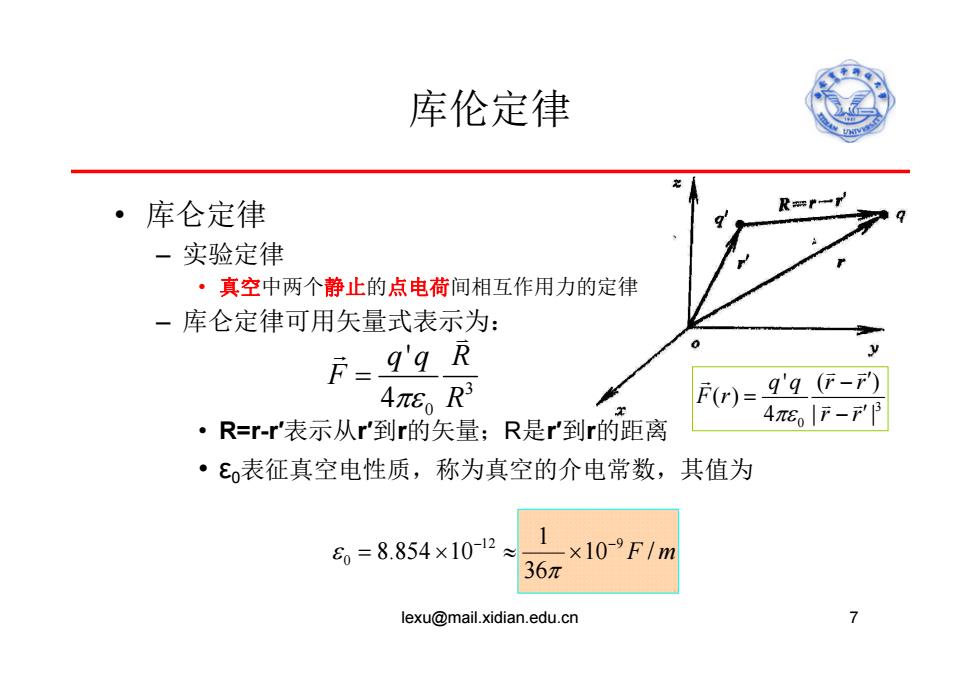
库伦定律 ·库仑定律 -实验定律 ·真空中两个静止的点电荷间相互作用力的定律 一库仑定律可用矢量式表示为： F=9'9R 4πER3 F)=g'9-F) ·R=r-r'表示从r'到r的矢量；R是r'到r的距离 48。|F-r'P ·￡表征真空电性质，称为真空的介电常数，其值为 6=8.854×10-12 x10-9F/m 36元 lexu@mail.xidian.edu.cn

库伦定律 • 库仑定律 – 实验定律 • 真空中两个静止的点电荷间相互作用力的定律 – 库仑定律可用矢量式表示为： • R=r-r′表示从r′到r的矢量；R是r′到r的距离 • ε0表征真空电性质，称为真空的介电常数，其值为 lexu@mail.xidian.edu.cn 7 3 0 ' 4 qq R F  R    10 F / m 36 1 8.854 10 12 9 0         3 0 '( ) ( ) 4 | | qq r r F r  r r          

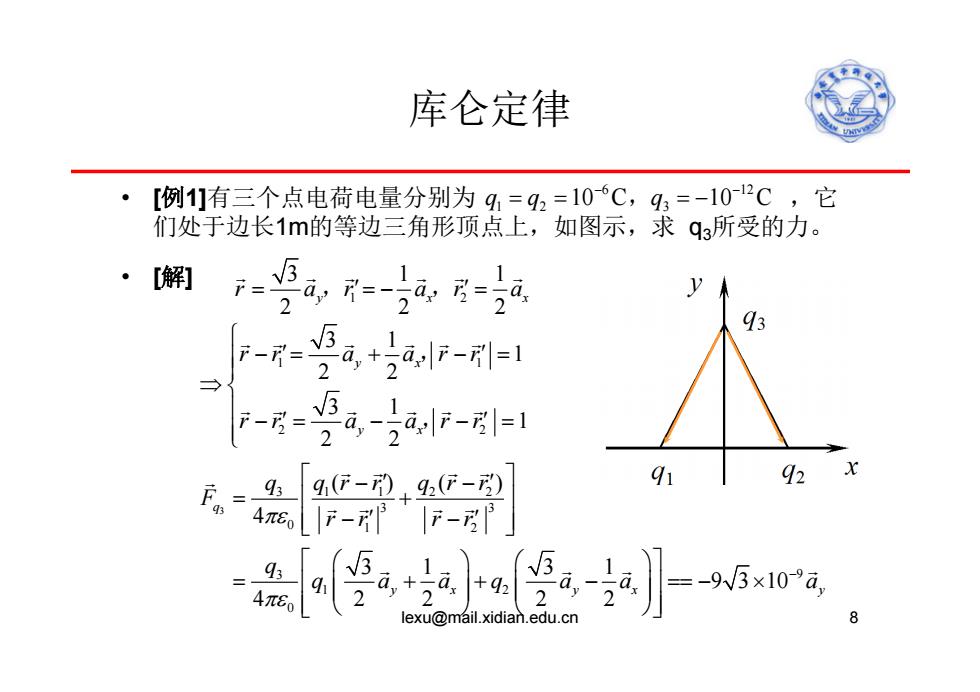
库仑定律 [例1]有三个点电荷电量分别为q=q2=106C,9=-102C,它 们处于边长1m的等边三角形顶点上，如图示，求q3所受的力。 ·解] F=5a 1 2 24F-=1 → FR- 24,F-1=1 a 2 9-+9(-2 91 92 4πe|F-F- .93 4π6l 9 2 =-96x10a lexu@mail.xidian.edu.cn

库仑定律 • [例1]有三个点电荷电量分别为 ，它 们处于边长1m的等边三角形顶点上，如图示，求 q3所受的力。 • [解] lexu@mail.xidian.edu.cn 8 6 12 12 3 qq q 10 C 10 C      ， 1 2 3 11 2 22 y xx r ar ar a          ， ， 1 1 2 2 3 1 1 2 2 3 1 1 2 2 y x y x rr a arr rr a arr                        ， ， 3 3 1 12 2 3 3 0 1 2 3 9 1 2 0 ()( ) 4 31 31 9 3 10 4 22 22 q yx yx y q qr r q r r F rr rr q q a aq a a a                                                          

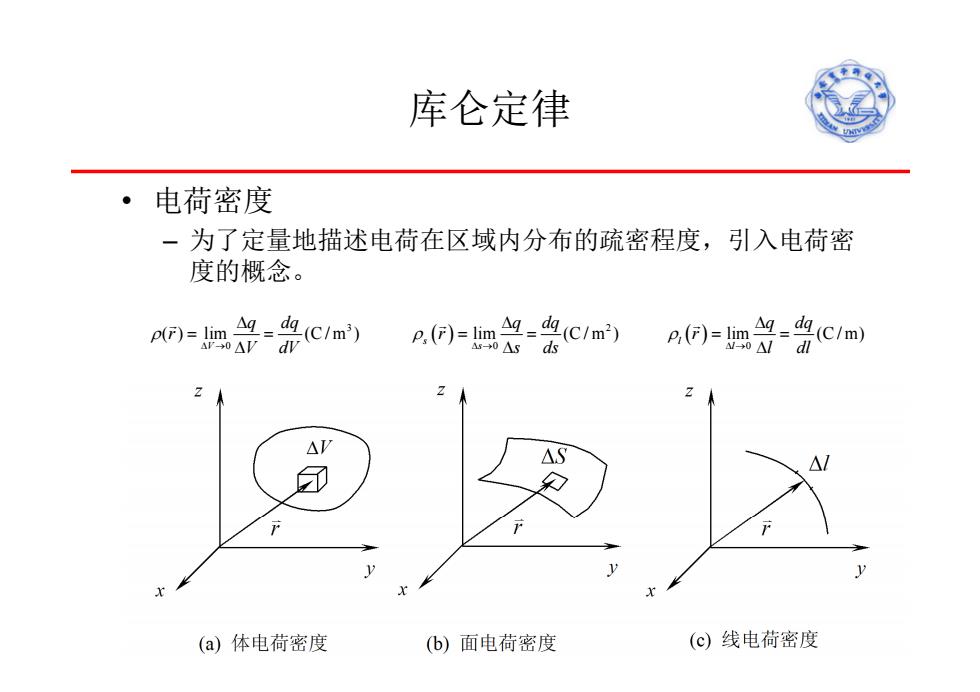
库仑定律 ·电荷密度 一为了定量地描述电荷在区域内分布的疏密程度，引入电荷密 度的概念。 p()=lim- g-d9(c1m3) r0△VdV p,()=im9-9c/m) (F)=limg=da (C/m) A→0△Sds →0△1d (a)体电荷密度 (b)面电荷密度 (c)线电荷密度

库仑定律 • 电荷密度 – 为了定量地描述电荷在区域内分布的疏密程度，引入电荷密 度的概念。 lexu@mail.xidian.edu.cn 9     3 2 0 00 ( ) lim (C / m ) lim (C / m ) lim (C / m) s l V sl q dq q dq q dq r rr V dV s ds l dl                 

库仑定律 ·分布电荷对点电荷的作用力 av' 一以体电荷为例 ·取处体积元dW;则dW'中电量为： dq'p(r")dv' ·将dg看作点电荷，则对电荷q的作用力为 dE,)=9-) 4π6F-F ·由迭加原理可知体积V对电荷q的作用力为： -1 lexu@mail.xidian.edu.cn 10

库仑定律 • 分布电荷对点电荷的作用力 – 以体电荷为例 • 取 处体积元 ，则 中电量为： • 将 看作点电荷，则对电荷q的作用力为： • 由迭加原理可知体积V对电荷q的作用力为： lexu@mail.xidian.edu.cn 10 r dV dV  dq r dV         dq       r dV r r q r r dF r q                 3 0 4             V q r dV r r q r r F r          3 0 4