
6.3 相对论的时空理论 1
1 6.3 相对论的时空理论

1.相对论时空结构 上一节中引入了两事件的间隔的概念。为了 简单,以第一事件为时空原点(0,0,0,0), 设第二事件时空坐标为,3,)。这两事件 的间隔定义为 s2=c2t2-x2-y2-z2=c2t2-r2 r=√x2+y2+z2为两事件的空间距离 2
2 上一节中引入了两事件的间隔的概念。为了 简单,以第一事件为时空原点(0,0,0,0), 设第二事件时空坐标为(x,y,z,t) 。这两事件 的间隔定义为 2 2 2 2 2 2 2 2 2 s = c t − x − y − z = c t − r r = x 2 + y 2 + z 2 为两事件的空间距离 1. 相对论时空结构

两事件的间隔可以取任何数值,区分三种情况 Q)g2=0, 2)82>0, (3)82ct。两事件的 事件可以用 事件通过低于 空间距离超过光 光波相联系。 光速的作用联 波在时间所能传 系。 播的距离。 从一个惯性系到另一个惯性系 的变换中,间隔2保持不变。 上述三种间隔的划分是绝对的。 不因参考系变换而改变。 3
3 两事件的间隔可以取任何数值,区分三种情况 (1) s 2=0 , 即r=ct。两 事件可以用 光波相联系。 (2) s 2>0, 即 rct。两事件的 空间距离超过光 波在时间t所能传 播的距离。 从一个惯性系到另一个惯性系 的变换中,间隔s 2保持不变。 上述三种间隔的划分是绝对的。 不因参考系变换而改变
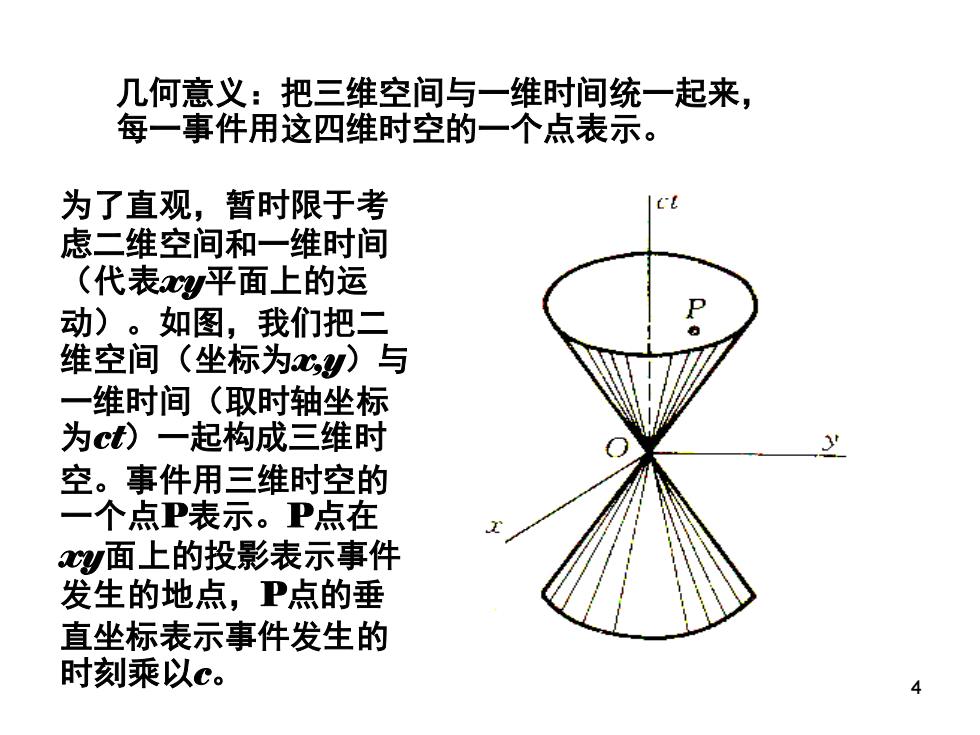
几何意义:把三维空间与一维时间统一起来, 每一事件用这四维时空的一个点表示。 为了直观,暂时限于考 虑二维空间和一维时间 (代表y平面上的运 动)。如图,我们把二 维空间(坐标为心)与 一维时间(取时轴坐标 为c)一起构成三维时 空。事件用三维时空的 一个点P表示。P点在 2以面上的投影表示事件 发生的地点,P点的垂 直坐标表示事件发生的 时刻乘以c
4 为了直观,暂时限于考 虑二维空间和一维时间 (代表xy平面上的运 动)。如图,我们把二 维空间(坐标为x,y)与 一维时间(取时轴坐标 为ct)一起构成三维时 空。事件用三维时空的 一个点P表示。P点在 xy面上的投影表示事件 发生的地点,P点的垂 直坐标表示事件发生的 时刻乘以c。 几何意义:把三维空间与一维时间统一起来, 每一事件用这四维时空的一个点表示
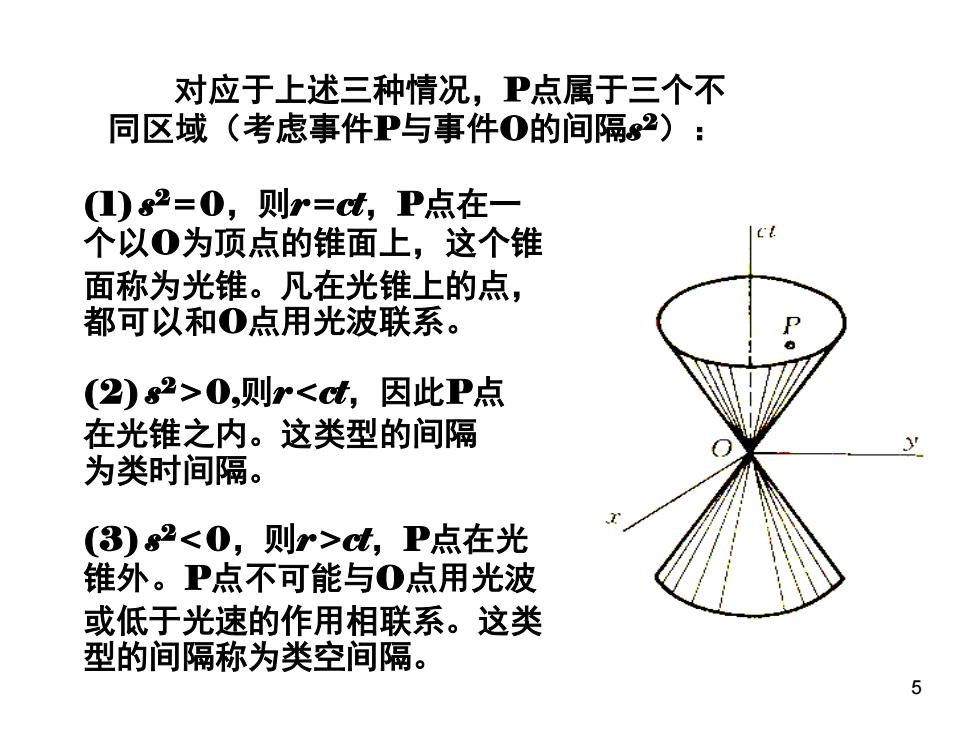
对应于上述三种情况,P点属于三个不 同区域(考虑事件P与事件0的间隔2): 1)2=0,则r=t,P点在一 个以0为顶点的锥面上,这个锥 面称为光锥。凡在光锥上的点, 都可以和0点用光波联系。 (2)2>0,则rt,P点在光 锥外。P点不可能与0点用光波 或低于光速的作用相联系。这类 型的间隔称为类空间隔。 5
5 对应于上述三种情况,P点属于三个不 同区域(考虑事件P与事件O的间隔s 2): (1) s 2=0,则r=ct,P点在一 个以O为顶点的锥面上,这个锥 面称为光锥。凡在光锥上的点, 都可以和O点用光波联系。 (2) s 2>0,则rct,P点在光 锥外。P点不可能与O点用光波 或低于光速的作用相联系。这类 型的间隔称为类空间隔

间隔的这种划分是绝对的,不因参考系 而转变。若对某参考系事件P在事件0的光 锥内,当变到另一参考系时,虽然P的空时 坐标都改变,但s不变。因此事件P在事件0 的光锥内。同样,若对某参考系P在0的光 锥外,则对所有参考系事件P都在事件0的 光锥外。 6
6 间隔的这种划分是绝对的,不因参考系 而转变。若对某参考系事件P在事件 O的光 锥内,当变到另一参考系时,虽然P的空时 坐标都改变,但s不变。因此事件P在事件O 的光锥内。同样,若对某参考系P在O的光 锥外,则对所有参考系事件P都在事件O的 光锥外

类时区域还可再分为两部分。 光锥的上下两半只有公共点0, 而洛伦兹变换保持时间正向不变, 因此光锥的上半部分和下半部分 不能互相变换。若事件P在0的上 半光锥内,则在其他参考系中它 保持在上半光锥内。 7
7 类时区域还可再分为两部分。 光锥的上下两半只有公共点O, 而洛伦兹变换保持时间正向不变, 因此光锥的上半部分和下半部分 不能互相变换。若事件P在O的上 半光锥内,则在其他参考系中它 保持在上半光锥内

概括起来,事件P相对于事件0的时空关系可作如 下的绝对分类: 1)类光间隔:2=0, (2)类时间隔:82>0, ()绝对未来,即P在0的上半光锥内; Cb)绝对过去,即P在0的下半光锥内; ()类空间隔:2<0,P与0绝对异地。 类时间隔和类空间隔是两种截然不同的 时空关系,下面分分别讨论。 8
8 概括起来,事件P相对于事件O的时空关系可作如 下的绝对分类: (1) 类光间隔:s 2=0, (2) 类时间隔:s 2>0, (3) 类空间隔:s 2<0,P与O绝对异地。 (a) 绝对未来,即P在O的上半光锥内; (b) 绝对过去,即P在O的下半光锥内; 类时间隔和类空间隔是两种截然不同的 时空关系,下面分分别讨论

2.因果律和相互作用的最 大传播速度 类时间隔 一小 切事物都是运动发展着的。事物发展有 一定因果联系,通过物质运动的联系,作为原 因的第一事件导致作为结果的第二事件。例如 通过无线电波的传播,发报者可以影响收报者 的行动。这种因果关系是绝对的,不依赖于参 考系而转移。时间概念就是从事物发展中抽象 出来的,正确的时空观必须反映事物发展的绝 对因果性。下面我们分析因果律在相对论时空 观中是这样体现出来的。 9
9 2. 因果律和相互作用的最 大传播速度 一切事物都是运动发展着的。事物发展有 一定因果联系,通过物质运动的联系,作为原 因的第一事件导致作为结果的第二事件。例如 通过无线电波的传播,发报者可以影响收报者 的行动。这种因果关系是绝对的,不依赖于参 考系而转移。时间概念就是从事物发展中抽象 出来的,正确的时空观必须反映事物发展的绝 对因果性。下面我们分析因果律在相对论时空 观中是这样体现出来的。 类时间隔

若事件P在0的上半光锥内(包括锥面), 即考虑类时间隔,则对任何惯性系P保持在0 的上半光锥内,即P为0的绝对未来。这种间 隔的特点是P与0可用光波或低于光速的作用 相联系。因此,如果不存在超光速的相互作 用,则两事件P与0发生因果关系的必要条件 是P处于0的光锥内,这样0与P的先后次序 在各参考系中相同,因而因果关系是绝对的。 10
10 若事件P在O的上半光锥内(包括锥面), 即考虑类时间隔,则对任何惯性系P保持在O 的上半光锥内,即P为O的绝对未来。这种间 隔的特点是P与O可用光波或低于光速的作用 相联系。因此,如果不存在超光速的相互作 用,则两事件P与O发生因果关系的必要条件 是P处于O的光锥内,这样O与P的先后次序 在各参考系中相同,因而因果关系是绝对的