
立体的投影
立体的投影

概述: 立体包含基本立体和组合体。柱、锥、球、圆环等 几何体是组成机件的基本体,基本体的组合称组合体。 平面立体 回转体 切割体的投影 相贯体的投影 ☑
平面立体 概述: 立体包含基本立体和组合体。柱、锥、球、圆环等 几何体是组成机件的基本体,基本体的组合称组合体。 回转体 切割体的投影 相贯体的投影
一、平面立体 平面立体一由若干个平面围成的实体。 工程上常用的平面立体是棱柱(主要是直棱柱)和棱锥 (棱台)。 棱柱 棱锥 棱台 图3-1平面立体 •平面立体侧表面的交线称为棱线。 ·若平面立体所有棱线互相平行,称为棱柱。 若平面立体所有棱线交于一点,称为棱锥。 ✉
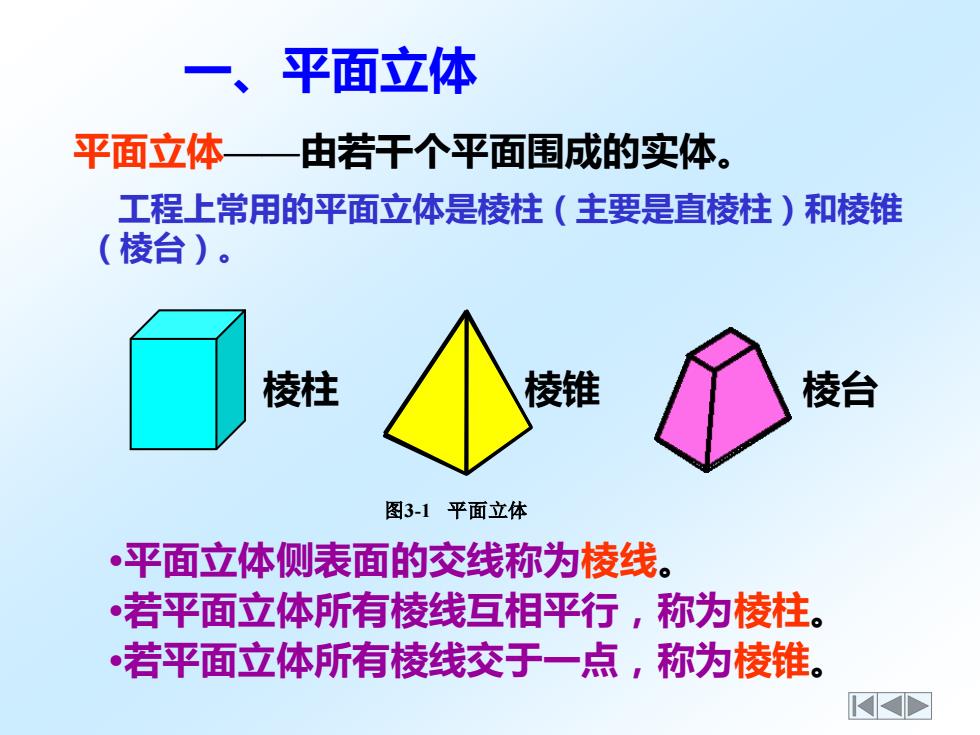
一、平面立体 平面立体——由若干个平面围成的实体。 工程上常用的平面立体是棱柱(主要是直棱柱)和棱锥 (棱台)。 •平面立体侧表面的交线称为棱线。 •若平面立体所有棱线互相平行,称为棱柱。 •若平面立体所有棱线交于一点,称为棱锥。 棱柱 棱锥 棱台 图3-1 平面立体

绘制平面立体的投影,即是绘制平面立体上所有 平面的投影,也就是绘制平面立体上各平面间的交 线(棱线)和各顶点(棱线的交点)的投影。 平面体的投影特征: ()体的三面投影图之间保持三等关系,适应整体和每一局部。 (②)体上各组成平面的投影,一般表现为一个封闭的线框,特殊 积聚为一直线。 (3)投影图上各线框的分界线,表示物体表面发生变化(凹、凸 或转折)
•绘制平面立体的投影,即是绘制平面立体上所有 平面的投影,也就是绘制平面立体上各平面间的交 线(棱线)和各顶点(棱线的交点)的投影。 平面体的投影特征: ⑴体的三面投影图之间保持三等关系,适应整体和每一局部。 ⑵体上各组成平面的投影,一般表现为一个封闭的线框,特殊 积聚为一直线。 ⑶投影图上各线框的分界线,表示物体表面发生变化(凹、凸 或转折)
棱柱 直棱柱—顶面和底面是两个全等且相互平行的多边 形(特征面),各侧面为矩形。 正棱柱—顶面和底面为正多边形的直棱柱。 1.棱柱的投影 ✉
直棱柱——顶面和底面是两个全等且相互平行的多边 形(特征面),各侧面为矩形。 正棱柱——顶面和底面为正多边形的直棱柱。 一、 棱柱 1. 棱柱的投影
1.棱柱的投影 分析:正六棱柱由顶面、底面和六个侧棱面组成。正六棱 柱的顶面、底面为水平面,在俯视图中反映实形。 3 作图: (a)直观图 (b)投影图 图3-2正六棱柱的投影 ✉
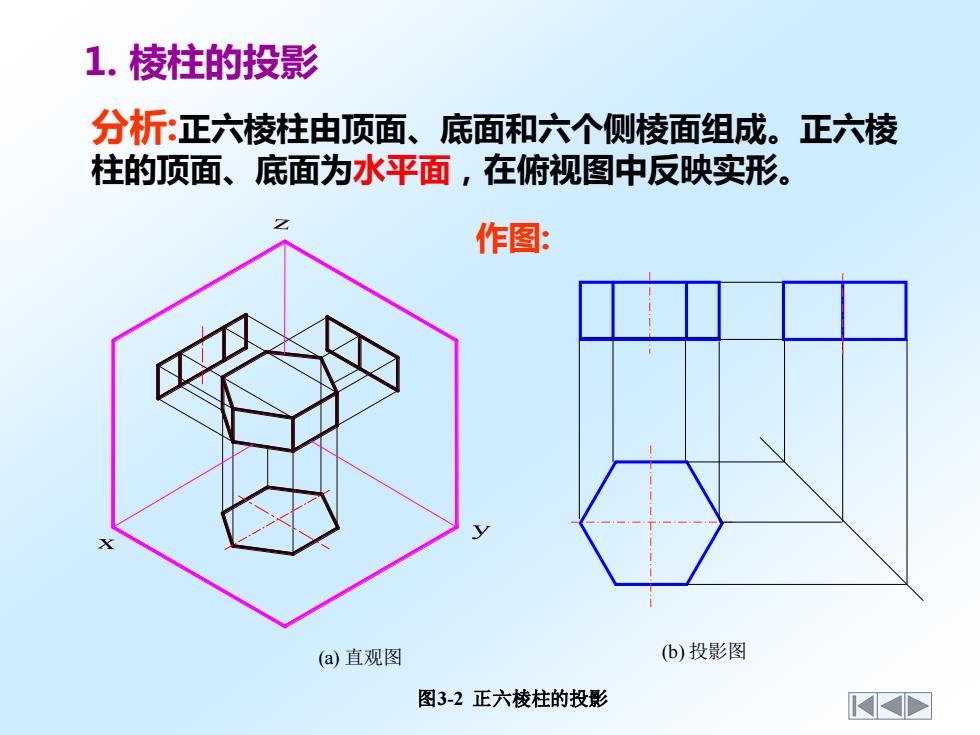
作图: 1. 棱柱的投影 分析:正六棱柱由顶面、底面和六个侧棱面组成。正六棱 柱的顶面、底面为水平面,在俯视图中反映实形。 (a) 直观图 (b) 投影图 图3-2 正六棱柱的投影

2.棱柱表面上点的投影 由于棱柱的表面都是平面,所以在棱柱的表面上取 点与在平面上取点的方法相同。 a(d) b( (a)直观图 ✉C
由于棱柱的表面都是平面,所以在棱柱的表面上取 点与在平面上取点的方法相同。 2. 棱柱表面上点的投影 (a) 直观图 M A B D C
已知六棱柱ABCD侧表面上点M的面投影m”, 求该点的H面投影m和W面投影m"。 m" a(d b(c) a(d) b(c) 点的可见性判别: 若点所在平面的投 (b)投影图 影可见点的投 (a)直观图 见来面的按影移 成看线,的 也可见
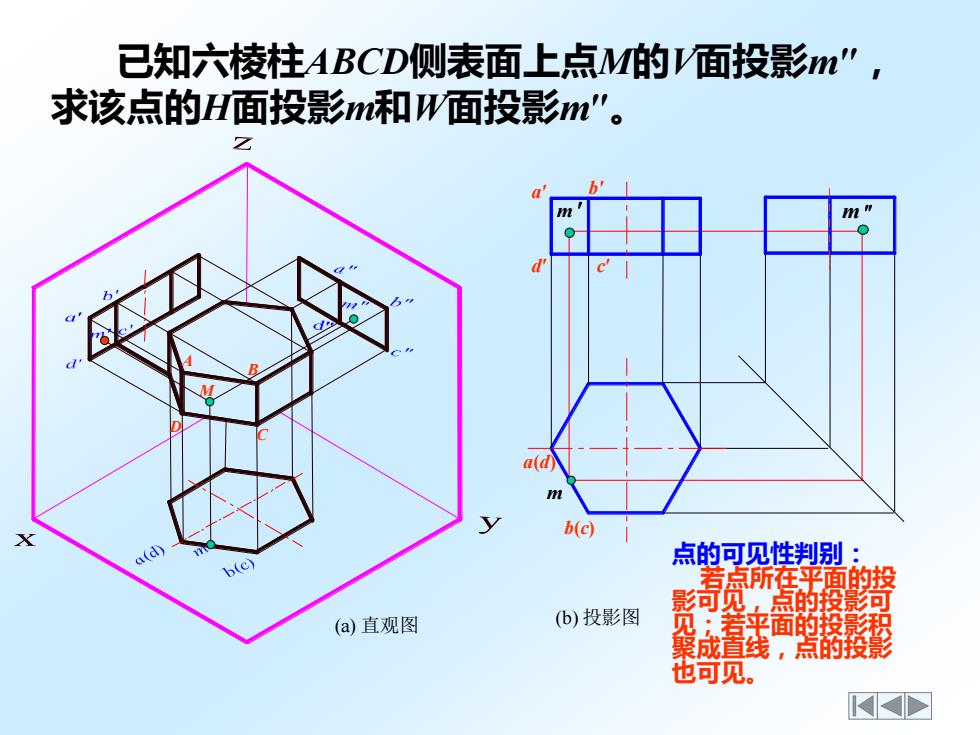
点的可见性判别: 若点所在平面的投 影可见,点的投影可 见;若平面的投影积 聚成直线,点的投影 也可见。 已知六棱柱ABCD侧表面上点M的V面投影m″ , 求该点的H面投影m和W面投影m″ 。 (b) 投影图 m (a) 直观图 a(d) b(c) a′ d′ b′ c′ M A B D C m m
二、棱锥 棱锥 底面是多边形,各侧面为若干具有公共顶点 的三角形。 正棱锥 底面为正多边形,各侧面是全等的等腰三角 形的棱锥。 1.棱锥的投影 S C B W✉D
1. 棱锥的投影 二、 棱锥 棱锥——底面是多边形,各侧面为若干具有公共顶点 的三角形。 正棱锥——底面为正多边形,各侧面是全等的等腰三角 形的棱锥。 A S B C
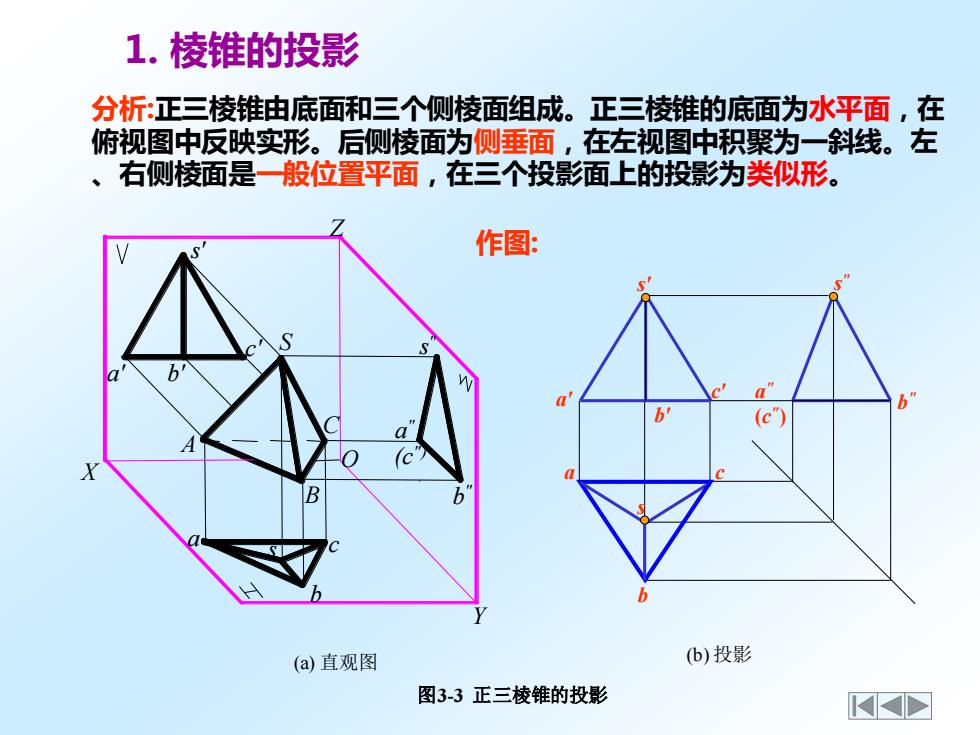
1.棱锥的投影 分析:正三棱锥由底面和三个侧棱面组成。正三棱锥的底面为水平面,在 俯视图中反映实形。后侧棱面为侧垂面,在左视图中积聚为一斜线。左 、右侧棱面是一般位置平面,在三个投影面上的投影为类似形。 作图: b a b b (c) (a)直观图 b)投影 图3-3正三棱锥的投影 ✉
1. 棱锥的投影 分析:正三棱锥由底面和三个侧棱面组成。正三棱锥的底面为水平面,在 俯视图中反映实形。后侧棱面为侧垂面,在左视图中积聚为一斜线。左 、右侧棱面是一般位置平面,在三个投影面上的投影为类似形。 作图: Y X Z s S " s' b' c' A C B b " a " b s c a a' O (c") (a) 直观图 (b) 投影 a b a′ b′ c′ c a " (c " ) b " 图3-3 正三棱锥的投影 s " s s′