
实验8固定均匀弦振动的研究 引言 在自然界当中,振动现象是广泛存在的振动是产生波动的根源,波动是振动的传播。固定均匀的 弦振动的传播,实际上是两个振幅相同的相干波的同一直线上沿相反方向传播的叠加,在一定条件 下便可形成驻波。本实验研究波的特征之一,干涉现象的特例一驻波。 实验目的 1、了解固定均匀振动传播的规律: 2、观察固定弦振动传播时形成验波的波形: 3、测定均匀弦振动上横波传播的速度 实验原理 设一均匀弦线,一端由劈尖A支住,另一端由劈尖B支撑。对均匀弦线扰动,引起弦线上质 点的振动,于是波动就由A端朝B端方向传播,称为入射波,再由B端反射沿弦线朝A端传播, 称为反射波。入射波与反射波在同一条弦线上沿相反方向传播时将相互干涉,移动劈尖B到适合 位置。弦线上的波就形成驻波。这 时,弦线上的波被分成几段且每段 波幅 波两端的点始终静止不动,而中间 的点振幅最大。这些始终静止的点 就称为波节,振幅最大的点就称为 =0 波腹。驻波的形成如下图所示。 设图中的两列波是沿X轴相向 方向传播的振幅相等、频率相同的 简谐波。向右传播的用细实线表示, 向左传播的用细虚线表示,它们的 X 1= 合成驻波用粗实线表示。由图可见, 两个波腹间的距离都是等于半个波 长,这可从波动方程推导出来。 下面用简谐表达式对驻波进行 定量描述。设沿X轴正方向传播的 波为入射波,沿X轴负方向传播的 波为反射波,取它们振动位相始终 相同的点作标原点,且在x=0处
1 实验 8 固定均匀弦振动的研究 引 言 在自然界当中,振动现象是广泛存在的,振动是产生波动的根源,波动是振动的传播。固定均匀的 弦振动的传播,实际上是两个振幅相同的相干波的同一直线上沿相反方向传播的叠加,在一定条件 下便可形成驻波。本实验研究波的特征之一,干涉现象的特例-驻波。 实验目的 1、了解固定均匀振动传播的规律; 2、观察固定弦振动传播时形成验波的波形; 3、测定均匀弦振动上横波传播的速度 实验原理 设一均匀弦线,一端由劈尖 A 支住,另一端由劈尖 B 支撑。对均匀弦线扰动,引起弦线上质 点的振动,于是波动就由 A 端朝 B 端方向传播,称为入射波,再由 B 端反射沿弦线朝 A 端传播, 称为反射波。入射波与反射波在同一条弦线上沿相反方向传播时将相互干涉,移动劈尖 B 到适合 位置。弦线上的波就形成驻波。这 时,弦线上的波被分成几段且每段 波两端的点始终静止不动,而中间 的点振幅最大。这些始终静止的点 就称为波节,振幅最大的点就称为 波腹。驻波的形成如下图所示。 设图中的两列波是沿 X 轴相向 方向传播的振幅相等、频率相同的 简谐波。向右传播的用细实线表示, 向左传播的用细虚线表示,它们的 合成驻波用粗实线表示。由图可见, 两个波腹间的距离都是等于半个波 长,这可从波动方程推导出来。 下面用简谐表达式对驻波进行 定量描述。设沿 X 轴正方向传播的 波为入射波,沿 X 轴负方向传播的 波为反射波,取它们振动位相始终 相同的点作标原点,且在 x 0处, 波 幅 波 节 A B X X X 4 T t 2 T t t 0 O O O 2

振动质点向上达最大位移时开始计时,则它们的波动方程为: 图1 y=Acos2aUn-之 h=4cos2(h+克 式中A为简谐波的振幅,∫为频率,入为波长,x为弦线上质点的坐标位置。 两波叠加后的合成波为驻波,其方程为: y=%+片=2Ac0sxc0s功 (1) 由式(1)可知,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为 24c0s2,即驻波的表与时间1无关,而与质点的位置x有关。 因为在波节处振幅为零,即 2a=2k+)月 (k=0,12,) 所以可得波节的位置为 x=(2k+) (2) 而相邻两波节之间的距离为: =号 (3) 又因为波腹处的质点振輻为最大,即 2r=k标 (k=0,1,2,.) 所以可得波腹的位置为: (4) 同理可知,相邻两波腹间的距离也是半个波长。因此,在驻波实验中,只要测得相邻两波节或相邻 两波腹间的距离,就能确定该波的波长。 由于固定弦的两端是用劈尖支住的,故两端点必为波节,所以,只有当弦线的两个固定端之间 的距离(弦长)等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件。其数 学表示式为: 1=n吃 (n=1,2,3 由此可得沿弦线传播的横波波长为
2 振动质点向上达最大位移时开始计时,则它们的波动方程为: 图 1 cos 2 ( ) 1 x y A ft cos 2 ( ) 2 x y A ft 式中 A 为简谐波的振幅, f 为频率, 为波长, x 为弦线上质点的坐标位置。 两波叠加后的合成波为驻波,其方程为: ft x y y y A 2 cos cos 1 2 (1) 由式(1)可知,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为 x 2Acos 2 ,即驻波的振幅与时间t 无关,而与质点的位置 x 有关。 因为在波节处振幅为零,即 cos 2 0 x ( 0, 1, 2, ) 2 2 (2k 1) k x 所以可得波节的位置为 4 (2 1) x k (2) 而相邻两波节之间的距离为: 2 1 1 xk x (3) 又因为波腹处的质点振幅为最大,即 cos 2 1 x 2 k (k 0, 1, 2,) x 所以可得波腹的位置为: 2 x k (4) 同理可知,相邻两波腹间的距离也是半个波长。因此,在驻波实验中,只要测得相邻两波节或相邻 两波腹间的距离,就能确定该波的波长。 由于固定弦的两端是用劈尖支住的,故两端点必为波节,所以,只有当弦线的两个固定端之间 的距离(弦长)等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件。其数 学表示式为: ( 1, 2, 3, ) 2 l n n 由此可得沿弦线传播的横波波长为
1=24 (5) 波动理论指出,弦线中横波的传播速度为 (6) 式中T为弦线中的张力,P为线密度,即单位长度的质量。 根据波速、频率及波长的普遍关系式)=几,将式(5)代入可得 v-r2 (7) 由式(6)和式(7)可得 (n=12,3,.) (8) 由式(8)可知,当给定T、p、I时,频率只有满足该式关系才能在弦线上形成驻波。同 理,当用外力(例如流过金属弦线中的交变电流在磁场中受到交变安培力的作用)去驱动弦线振动 时,外力的频率必须与这些频率一致,才会促使弦振动的传播形成驻波。 实验仪器 0 3 图2 1、6香焦插头座(接弦线) 2、频率显示 3、电源开关 4、频率调节旋钮 5、磁钢 7、砝码盘 8、米尺
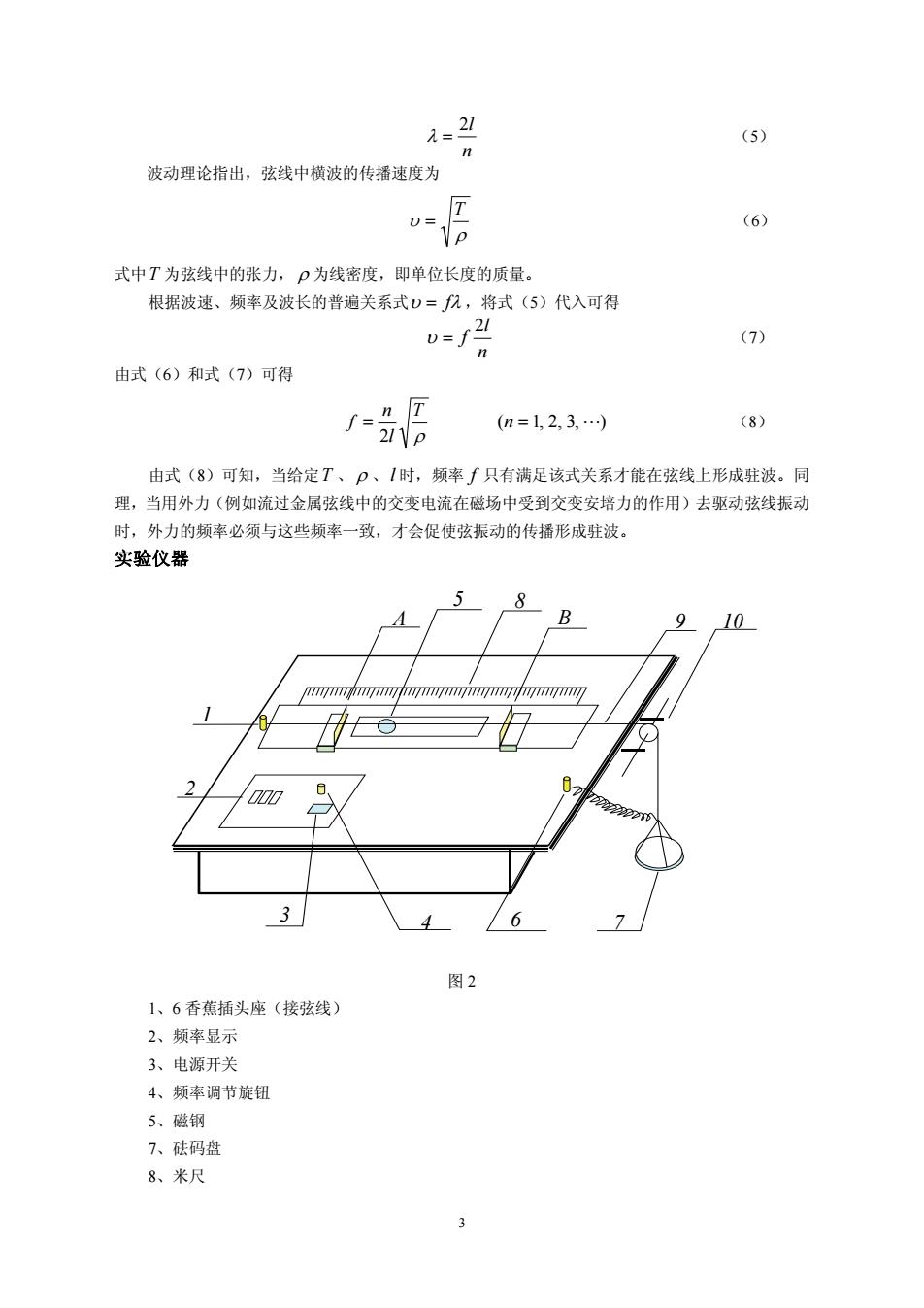
3 n 2l (5) 波动理论指出,弦线中横波的传播速度为 T (6) 式中T 为弦线中的张力, 为线密度,即单位长度的质量。 根据波速、频率及波长的普遍关系式 f ,将式(5)代入可得 n l f 2 (7) 由式(6)和式(7)可得 ( 1, 2, 3, ) 2 n T l n f (8) 由式(8)可知,当给定T 、 、l 时,频率 f 只有满足该式关系才能在弦线上形成驻波。同 理,当用外力(例如流过金属弦线中的交变电流在磁场中受到交变安培力的作用)去驱动弦线振动 时,外力的频率必须与这些频率一致,才会促使弦振动的传播形成驻波。 实验仪器 图 2 1、6 香蕉插头座(接弦线) 2、频率显示 3、电源开关 4、频率调节旋钮 5、磁钢 7、砝码盘 8、米尺 1 2 3 4 6 7 B 9 10 5 A 8

9、弦线 10、滑轮及托架 A、B两劈尖(滑块) 实验装置如上图所示。实验时在1和6间接上弦线,将电源接通。这样,在磁场作用下,通过 正弦交变电流的弦线就会振动。根据需要,可以调节频率调节旋钮,从显示器上读出所需频率。移 动磁铁的位置,使弦振动调整到最佳状态(使弦振动的振动面与磁场方向完全垂直)。移动劈尖的 位置,可以改变弦长。 实验内容 1、测定弦线的线密度p 选取频率∫=100Hz,张力T由40.0g砝码挂在弦线的一端产生。调节劈尖A\B之间的距离, 使弦线上依次出现单段、两段及三段驻波,并记录相应的弦长↓,由式(8)算出P,=(i=1,2,3), 求出平均值p。 2、在频率f一定的条件下,改变张力T的大小,测量弦线上横波的传播速度) 选取频率∫=75H,张力T仍由砝码挂在弦线的一端产生。以30.0g砝码为起点,逐次增加 5.0g直至55.0g为止。在各张力作用下调节弦长1,使弦上出现n=1、n=2个驻波段。记录相应 的T、n、1值,由式(7)计算弦上横波速度D,。 3、在张力T一定的条件下,改变频率∫,测量弦线上横波的传播速度, 将40.0g砝码挂在弦线一端,选取频率∫分别为50Hz、75Hz、100Hz、125Hz、150Hz,调节 弦长l,仍使弦上出现n=1、n=2个驻波段。记录相应的f、n、1值,由式(7)计算弦上横波 速度vr。 思考题 1、在图1中,除了波节和波腹外,你能指出驻波还有什么特征吗? 2、在本实验中,产生驻波的条件是什么? 3、来自两个波腹的两列波,沿同一直线作相向进行时,能否形成驻波?为什么? 注意事项 1、改变挂在弦线一端的砝码时,要使砝码稳定后再进行测量。 2、在移动劈尖调整驻波段时,磁铁应在两劈尖之间,且不能处于波节位置;要等波形稳定后, 再记录数据。 3、张力T大小要计入托盘的质量(实验室提供的砝码托盘为10.0g)
4 9、弦线 10、滑轮及托架 A、B 两劈尖(滑块) 实验装置如上图所示。实验时在 1 和 6 间接上弦线,将电源接通。这样,在磁场作用下,通过 正弦交变电流的弦线就会振动。根据需要,可以调节频率调节旋钮,从显示器上读出所需频率。移 动磁铁的位置,使弦振动调整到最佳状态(使弦振动的振动面与磁场方向完全垂直)。移动劈尖的 位置,可以改变弦长。 实验内容 1、测定弦线的线密度 选取频率 f 100Hz ,张力T 由 40.0g 砝码挂在弦线的一端产生。调节劈尖 A \ B 之间的距离, 使弦线上依次出现单段、两段及三段驻波,并记录相应的弦长 i l ,由式(8)算出 (i 1, 2, 3) i , 求出平均值 。 2、在频率 f 一定的条件下,改变张力T 的大小,测量弦线上横波的传播速度 f 选取频率 f 75Hz ,张力 T 仍由砝码挂在弦线的一端产生。以 30.0g 砝码为起点,逐次增加 5.0g 直至 55.0g 为止。在各张力作用下调节弦长l ,使弦上出现 n 1、 n 2 个驻波段。记录相应 的T 、 n 、l 值,由式(7)计算弦上横波速度 f 。 3、在张力T 一定的条件下,改变频率 f ,测量弦线上横波的传播速度T 将 40.0g 砝码挂在弦线一端,选取频率 f 分别为 50Hz、75Hz、100Hz、125Hz、150Hz,调节 弦长l ,仍使弦上出现 n 1、n 2 个驻波段。记录相应的 f 、n 、l 值,由式(7)计算弦上横波 速度T 。 思考题 1、在图 1 中,除了波节和波腹外,你能指出驻波还有什么特征吗? 2、在本实验中,产生驻波的条件是什么? 3、来自两个波腹的两列波,沿同一直线作相向进行时,能否形成驻波?为什么? 注意事项 1、改变挂在弦线一端的砝码时,要使砝码稳定后再进行测量。 2、在移动劈尖调整驻波段时,磁铁应在两劈尖之间,且不能处于波节位置;要等波形稳定后, 再记录数据。 3、张力 T 大小要计入托盘的质量(实验室提供的砝码托盘为 10.0g)