
实验20光的等厚干涉 引言 牛顿环是牛顿在1675年制作天文望远镜时,偶然将一个望远镜的物镜放在平板玻 璃上发现的。牛顿环是一种典型的等厚干涉,是分振幅法产生的定域干涉。利用它检 验一些光学元件的球面度、平面度、光洁度缺陷以及机械零件的内应力分布等,在科 学研究、工业生产检测技术中具有广泛的用途。 实验目的 1、加深对光的等厚干涉原理的理解。 2、观察和研究等厚干涉现象及其特点。 3、练习用干涉法测量透镜的曲率半径、微小直径(或厚度)。 4.·设计用干涉法测量液体的折射率。 实验原理 利用透明薄膜上下两表面对入射光的依次反射,入射光的振幅将被分解成有一定光程差的几个 部分。若两束反射光相遇时的光程差取决于产生反射光的透明薄膜厚度,则同一干涉条纹所对应的 薄膜厚度相同,这就是等厚干涉。牛顿环和劈尖干涉都是典型的等厚干涉。 1.牛顿环 将一块平凸透镜的凸面放在一块光学平板玻璃上,因而在它们之间形成以接触点0为中心向 四周逐渐增厚的空气薄膜,离0点等距离处厚度相同。如图】()所示。当光垂直入射时,其中 有一部分光线在空气膜的上表面反射,一部分在空气膜的下表面反射,因此产生两束具有一定光程 差的相干光,当它们相遇后就产生干涉现象。由于空气膜厚度相等处是以接触点为圆心的同心圆, 即以接触点为圆心的同一圆周上各点的光程差相等,故干涉条纹是一系列以接触点为圆心的明暗相 间的同心圆,如图1(b)所示。这种干涉现象称为牛顿环。 由光路分析可知,与k级条纹对应的两束相干光的光程差为 δ=2e+ (1)
1 实验 20 光的等厚干涉 引 言 牛顿环是牛顿在 1675 年制作天文望远镜时,偶然将一个望远镜的物镜放在平板玻 璃上发现的。牛顿环是一种典型的等厚干涉,是分振幅法产生的定域干涉。利用它检 验一些光学元件的球面度、平面度、光洁度缺陷以及机械零件的内应力分布等,在科 学研究、工业生产检测技术中具有广泛的用途。 实验目的 1、加深对光的等厚干涉原理的理解。 2、观察和研究等厚干涉现象及其特点。 3、练习用干涉法测量透镜的曲率半径、微小直径(或厚度)。 4.* 设计用干涉法测量液体的折射率。 实验原理 利用透明薄膜上下两表面对入射光的依次反射,入射光的振幅将被分解成有一定光程差的几个 部分。若两束反射光相遇时的光程差取决于产生反射光的透明薄膜厚度,则同一干涉条纹所对应的 薄膜厚度相同,这就是等厚干涉。牛顿环和劈尖干涉都是典型的等厚干涉。 1.牛顿环 将一块平凸透镜的凸面放在一块光学平板玻璃上,因而在它们之间形成以接触点 O 为中心向 四周逐渐增厚的空气薄膜,离 O 点等距离处厚度相同。如图 1(a)所示。当光垂直入射时,其中 有一部分光线在空气膜的上表面反射,一部分在空气膜的下表面反射,因此产生两束具有一定光程 差的相干光,当它们相遇后就产生干涉现象。由于空气膜厚度相等处是以接触点为圆心的同心圆, 即以接触点为圆心的同一圆周上各点的光程差相等,故干涉条纹是一系列以接触点为圆心的明暗相 间的同心圆,如图 1(b)所示。这种干涉现象称为牛顿环。 由光路分析可知,与 k 级条纹对应的两束相干光的光程差为 2 2 k e (1)
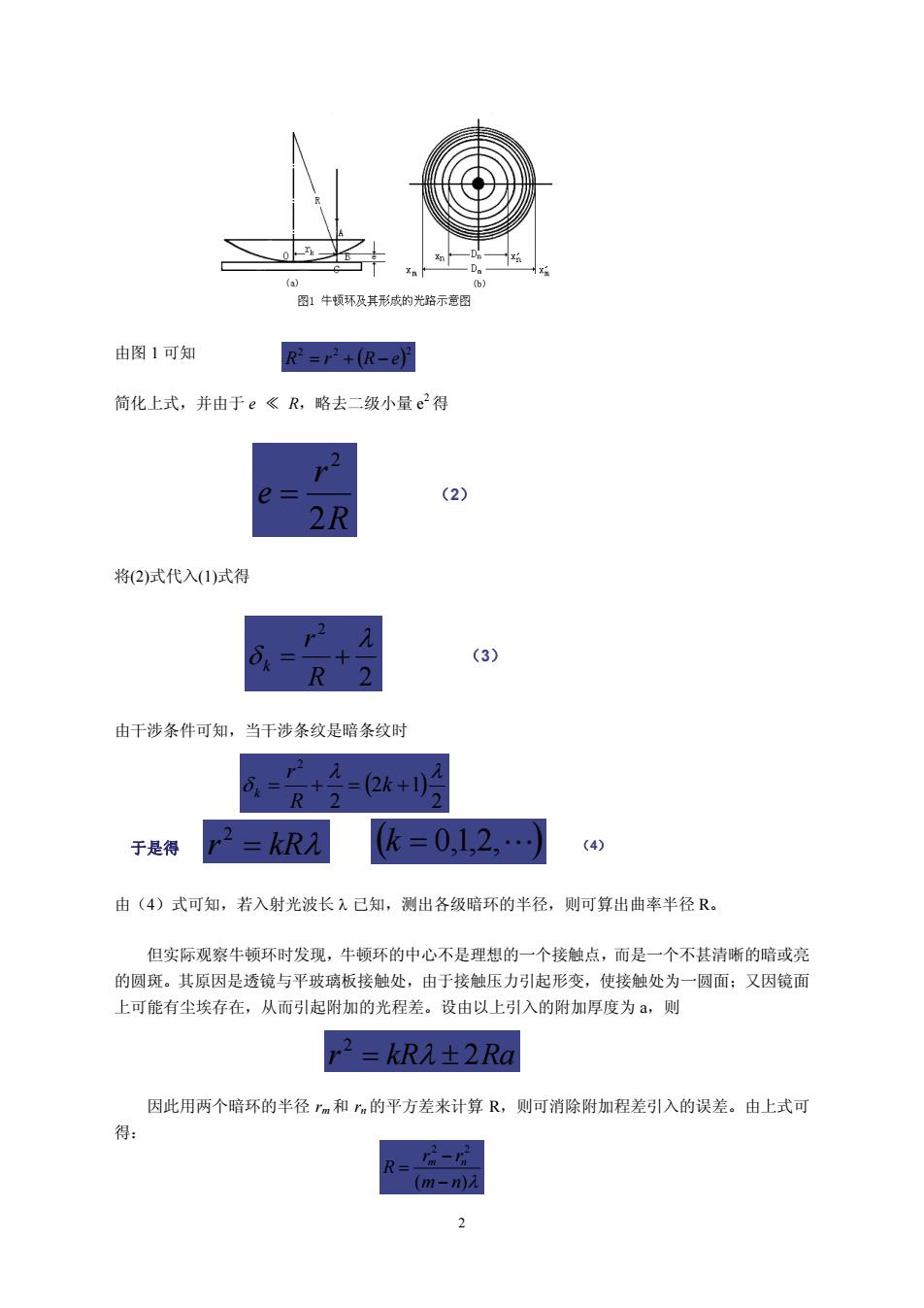
图】牛顿环及其形成的光路示意图 由图1可知 R=P2+R-e明 简化上式,并由于e《R,略去二级小最e2得 (2) 2R 将(2)式代入(1)式得 2 (3) R 由干涉条件可知,当干涉条纹是暗条纹时 =(2k+1)月 于是得 k=0,12,】 (4) 由(4)式可知,若入射光波长入已知,测出各级暗环的半径,则可算出曲率半径R。 但实际观察牛顺环时发现,牛顿领环的中心不是理想的一个接触点,而是一个不其清晰的暗或亮 的圆斑。其原因是透镜与平玻璃板接触处,由于接触压力引起形变,使接触处为一圆面:又因镜面 上可能有尘埃存在,从而引起附加的光程差。设由以上引入的附加厚度为a,则 r2=kR1±2Ra 因此用两个暗环的半径r和的平方差来计算R,则可消除附加程差引入的误差。由上式可 r-r
2 由图 1 可知 简化上式,并由于 e ≪ R,略去二级小量 e 2 得 将(2)式代入(1)式得 由干涉条件可知,当干涉条纹是暗条纹时 由(4)式可知,若入射光波长 已知,测出各级暗环的半径,则可算出曲率半径 R。 但实际观察牛顿环时发现,牛顿环的中心不是理想的一个接触点,而是一个不甚清晰的暗或亮 的圆斑。其原因是透镜与平玻璃板接触处,由于接触压力引起形变,使接触处为一圆面;又因镜面 上可能有尘埃存在,从而引起附加的光程差。设由以上引入的附加厚度为 a,则 因此用两个暗环的半径 rm 和 rn 的平方差来计算 R,则可消除附加程差引入的误差。由上式可 得: R r e 2 2 (2) 2 2 R r k (3) r kR 2 k 0,1,2, (4) 2 2 2 R r R e 2 2 1 2 2 k R r k r kR 2Ra 2 ( ) 2 2 m n r r R m n 于是得

又因为暗环圆心不易确定,故可用暗环的直径代替半径,得: D:-D2 (5) 4m-)2 2.劈尖 劈尖干涉装置如图2()所示。将两块光学平板玻璃迭在一起,在一端放入一薄片或细丝 则在两玻璃板间形成一空气劈尖,当用单色光垂直照射时,在劈尖薄膜的上下两表面反射的两束相 干光相遇时发生干涉。两者光程差二2+2,产生的干涉条纹是一簇与玻璃板交线相平行的等间距 明暗相间的平行直条纹,如图2(b)所示。 (a) (b) 图2劈尖干涉 显然,当 =2e+2 =(2k+1) k=012 时,为暗条纹。与k级暗条纹对应的薄膜厚度为: (6) 3.液体折射率的测量(设计) 实验要求:设计好测量方案,包括实验原理,公式的推导,实验步骤,数据表格等。 实验提示:可在平凸玻璃和平板玻璃之间滴入待测液体,此时液体薄膜上下两表面所反射光的 光程差六2ne+2,n是液体的折射率。根据干涉原理可推导出液体折射率公式。 实验仪器 读数显微镜、牛顿环测试仪、劈尖玻璃、钠光灯 仪器简介
3 又因为暗环圆心不易确定,故可用暗环的直径代替半径,得: (5) 2.劈尖 劈尖干涉装置如图 2(a)所示。将两块光学平板玻璃迭在一起,在一端放入一薄片或细丝, 则在两玻璃板间形成一空气劈尖,当用单色光垂直照射时,在劈尖薄膜的上下两表面反射的两束相 干光相遇时发生干涉。两者光程差 =2e+/2,产生的干涉条纹是一簇与玻璃板交线相平行的等间距 明暗相间的平行直条纹,如图 2(b)所示。 显然,当 时,为暗条纹。与 k 级暗条纹对应的薄膜厚度为: 3.液体折射率的测量(设计) 实验要求:设计好测量方案,包括实验原理,公式的推导,实验步骤,数据表格等。 实验提示:可在平凸玻璃和平板玻璃之间滴入待测液体,此时液体薄膜上下两表面所反射光的 光程差 =2ne+/2,n 是液体的折射率。根据干涉原理可推导出液体折射率公式。 实验仪器 读数显微镜、牛顿环测试仪、劈尖玻璃、钠光灯 仪器简介 2 2 1 2 2 k e k k 0,1,2 2 e k (6) 4( ) 2 2 m n D D R m n

1.读数显微镜 日镜 读数标尺 调焦手轮 读散 载物平台 测微鼓轮 2.牛顿环装置 牛顿环装置是由平凸透镜L和磨光的平玻璃板P叠合装在金属框架F中构成(图3)。框架边 上有三个螺旋H,用以调节L和P之间的接触,以改变干涉环纹的形状和位置。调节H时,螺旋 不可旋得过紧,以免接触压力过大引起透镜弹性形变,甚至损坏透镜。 图3牛顿环装置 实验内容 1.根据牛顿环测量透镜的曲率半径 (1)按图4安放实验仪器。 (2)调节牛倾环仪边框上三个螺旋,使在牛顿环仪中心出现一组同心干涉环。将牛顿环仪放在显 微镜的平台上,调节45°玻璃板,以便获得最大的照度
4 1.读数显微镜 2.牛顿环装置 牛顿环装置是由平凸透镜 L 和磨光的平玻璃板 P 叠合装在金属框架 F 中构成(图 3)。框架边 上有三个螺旋 H,用以调节 L 和 P 之间的接触,以改变干涉环纹的形状和位置。调节 H 时,螺旋 不可旋得过紧,以免接触压力过大引起透镜弹性形变,甚至损坏透镜。 实验内容 1.根据牛顿环测量透镜的曲率半径 (1)按图 4 安放实验仪器。 (2)调节牛顿环仪边框上三个螺旋,使在牛顿环仪中心出现一组同心干涉环。将牛顿环仪放在显 微镜的平台上,调节 45玻璃板,以便获得最大的照度。 目镜 物镜 调焦手轮 测微鼓轮 读数标尺 读数盘 载物平台

图4实验装置图 (3)调节读数显微镜调焦手轮,使显微镜筒自下而上缓慢地上升,直至在显微镜内能看到清晰的 干涉条纹的像。适当移动牛顿环位置,使干涉条纹的中央暗区在显微镜叉丝的正下方,观察干涉条 纹是否在显微镜的读数范围内,以便测量。 (4)转动测微鼓轮,先使镜筒由牛顿环中心向左移动,顾序数到第3引暗环,再反向至第30暗环 并使竖直义丝对准暗环中间,依次测量各暗环左右两侧的位置,将数据填入表中。在整个测量过程 中,鼓轮只能沿同一个方向旋转,中途不能倒转。显然,某环左右位置读数之差即为该环的直径。 用逐差法求出R,并计算误差。 数据记录表 大环 2R- 2.用劈尖干涉法则微小厚度d (1)将被测薄片(或细丝)夹在两块平板玻璃的之间,形成劈尖,然后置于读数显微镜载物台上。 (2)用读数显微镜测出x条(如20条)暗条纹间的垂直距离x,再测出棱边到细丝所在处的总长 度L,求出d
5 (3)调节读数显微镜调焦手轮,使显微镜筒自下而上缓慢地上升,直至在显微镜内能看到清晰的 干涉条纹的像。适当移动牛顿环位置,使干涉条纹的中央暗区在显微镜叉丝的正下方,观察干涉条 纹是否在显微镜的读数范围内,以便测量。 (4)转动测微鼓轮,先使镜筒由牛顿环中心向左移动,顺序数到第 31 暗环,再反向至第 30 暗环 并使竖直叉丝对准暗环中间,依次测量各暗环左右两侧的位置,将数据填入表中。在整个测量过程 中,鼓轮只能沿同一个方向旋转,中途不能倒转。显然,某环左右位置读数之差即为该环的直径。 用逐差法求出 R,并计算误差。 数据记录表 2.用劈尖干涉法则微小厚度 d (1)将被测薄片(或细丝)夹在两块平板玻璃的之间,形成劈尖,然后置于读数显微镜载物台上。 (2)用读数显微镜测出 x 条(如 20 条)暗条纹间的垂直距离 lx,再测出棱边到细丝所在处的总长 度 L,求出 d。 环数 m 30 29 28 27 26 左 右 大环直径/mm Dm 环数 n 25 24 23 22 21 左 右 小环直径/mm Dn 大环直径平方 Dm 2 小环直径平方 Dn 2 环的位置/mm 环的位置/mm m n D D Ri m n 4 2 2 1 1 2 u R R n n n i R i

2 由图2几何关系得 导出 (3)重复步骤2,各测三次,将数据填入自拟表格中。求其平均值。 3.*根据设计好的方案测液体的折射率 思考题 1.试比较牛顿环和劈尖的干涉条纹的异同点。 2透射光的牛顿环是如何形成的?如何观察?它与反射光的牛顿环在明暗上有何关系,为什么? 3.在牛顿环实验中,假如平板玻璃上有微小的凸起,则凸起处空气薄膜的厚度减小,导致等厚干涉 条纹发生畸变。试问这时牛顿环将局部内凹还是局部外凸?为什么? 4用白光照射时能否看到牛顿环和劈尖干涉条纹?此时条纹有何特征? 5.为什么说读数显微镜测量的是牛顿环的直径,而不是显微镜内牛顿环的放大象的直径?如果改变 显微镜的放大倍率,是否会影响测量的结果? 6.在牛顿环实验中,若不是测牛顿环直径,而是测弦长是否可以?试从理论上加以说明。 注意事项 1.调焦时,显微镜筒应自下而上缓慢的上升,避免显微镜筒压坏45°玻璃片(或损坏牛顿环装置)。 2.每次测量时,鼓轮应沿一个方向转动,中途不可倒转。(为什么?)
6 (3)重复步骤 2,各测三次,将数据填入自拟表格中。求其平均值 。 3.* 根据设计好的方案测液体的折射率 思考题 1.试比较牛顿环和劈尖的干涉条纹的异同点。 2.透射光的牛顿环是如何形成的?如何观察?它与反射光的牛顿环在明暗上有何关系,为什么? 3.在牛顿环实验中,假如平板玻璃上有微小的凸起,则凸起处空气薄膜的厚度减小,导致等厚干涉 条纹发生畸变。试问这时牛顿环将局部内凹还是局部外凸?为什么? 4.用白光照射时能否看到牛顿环和劈尖干涉条纹?此时条纹有何特征? 5.为什么说读数显微镜测量的是牛顿环的直径,而不是显微镜内牛顿环的放大象的直径?如果改变 显微镜的放大倍率,是否会影响测量的结果? 6.在牛顿环实验中,若不是测牛顿环直径,而是测弦长是否可以?试从理论上加以说明。 注意事项 1.调焦时,显微镜筒应自下而上缓慢的上升,避免显微镜筒压坏 45玻璃片(或损坏牛顿环装置)。 2.每次测量时,鼓轮应沿一个方向转动,中途不可倒转。(为什么?) 2 xl xL d L l x d x 2 由图2几何关系得 导出