
实验44RC串联电路 RC串联电路在接通或断开直流电源的瞬间,相当于受到阶跃电压的影响,电路对此要 作出响应,会从一个稳定态转变到另一个稳定态,这个转变过程称为暂态过程。此过程变化 快慢是由电路中各元件的量值和特性决定的,描述暂态变化快慢的特性参数是放电电路的时 间常数或半衰期。 一个实际电路总可简化成某种等效电路,常见的等效电路有RC或LC电路。本实验 研究C串联电路在暂态过程中,不同参数对电流、电压的影响。通过对暂态过程的研究, 可以积极控制和利用暂态现象。研究C串联电路暂态过程通常用直流法或交流法,直流法 包括冲击法和电压法,交流法中有示波器观测法。 RC串联电路的暂态特性在电子电路中有许多用途,例如:可起延迟作用、积分作用、 耦合作用、隔直流作用等等。 【实验目的】 1.学习如何通过实验方法研究有关RC串联电路的暂态过程。 2.通过研究RC串联电路暂态过程,加深对电容特性的认识和对RC串联电路特性的理解。 3.提高对RC串联电路暂态过程的分析技能。 4.根据对实验现象的分析,学习和了解进行科学实验的一般程序和方法。 【实验要求】 1.用计算机进行辅助设计,选择最佳的实验方案,最终由实验验证设计的合理性、正确性。 2.用电压表测Uc(t)(或Ut)来研究RC串联电路充放电电压(或电流)曲线。 3.研究不同R(或C)的RC串联电路的各种特性。 4.由实验测量时间常数t,将此值与由理论公式求得的x值进行比较。 5.用示波器测试RC串联电路的电流值与电容量。 6.用李萨如图形测量相位。 【实验提示】 1.RC串联电路的充放电过程 电阻、电容是电路的基本元件。在阻容串联电路中,接通或断开直流电源时,电路往往 产生从一种状态过渡到另一种稳定状态的暂态过程,可以用示波器观测这种瞬变过程。用示 波器测量RC串联电路中的电流值和电容量可采用图1所示的电路来测量。用示波器测量出 电阻R两端的电压42见图1,则可知RC串联电路中的电流 i= (1) 再用示波器按图2所示电路测量出电容器C两端的电压。,因为电源按原频率)变化时, 有 %=i. @C 由(1)和(2)式可求得C值: C=Ug 3 oRuc 实验中测量出山,和给定的R,O值,就可以求得i和C的值
实验 44 RC 串联电路 RC 串联电路在接通或断开直流电源的瞬间,相当于受到阶跃电压的影响,电路对此要 作出响应,会从一个稳定态转变到另一个稳定态,这个转变过程称为暂态过程。此过程变化 快慢是由电路中各元件的量值和特性决定的,描述暂态变化快慢的特性参数是放电电路的时 间常数或半衰期。 一个实际电路总可简化成某种等效电路,常见的等效电路有 RC 或 RLC 电路。本实验 研究 RC 串联电路在暂态过程中,不同参数对电流、电压的影响。通过对暂态过程的研究, 可以积极控制和利用暂态现象。研究 RC 串联电路暂态过程通常用直流法或交流法,直流法 包括冲击法和电压法,交流法中有示波器观测法。 RC 串联电路的暂态特性在电子电路中有许多用途,例如:可起延迟作用、积分作用、 耦合作用、隔直流作用等等。 【实验目的】 1.学习如何通过实验方法研究有关 RC 串联电路的暂态过程。 2.通过研究 RC 串联电路暂态过程,加深对电容特性的认识和对 RC 串联电路特性的理解。 3.提高对 RC 串联电路暂态过程的分析技能。 4.根据对实验现象的分析,学习和了解进行科学实验的一般程序和方法。 【实验要求】 1.用计算机进行辅助设计,选择最佳的实验方案,最终由实验验证设计的合理性、正确性。 2.用电压表测 Uc(t)(或 UR(t))来研究 RC 串联电路充放电电压(或电流)曲线。 3.研究不同 R(或 C)的 RC 串联电路的各种特性。 4.由实验测量时间常数 ,将此值与由理论公式求得的 值进行比较。 5.用示波器测试 RC 串联电路的电流值与电容量。 6.用李萨如图形测量相位。 【实验提示】 1.RC 串联电路的充放电过程 电阻、电容是电路的基本元件。在阻容串联电路中,接通或断开直流电源时,电路往往 产生从一种状态过渡到另一种稳定状态的暂态过程,可以用示波器观测这种瞬变过程。用示 波器测量 RC 串联电路中的电流值和电容量可采用图 1 所示的电路来测量。用示波器测量出 电阻 R 两端的电压 R u 见图 1,则可知 RC 串联电路中的电流 R u i R (1) 再用示波器按图 2 所示电路测量出电容器 C 两端的电压 C u ,因为电源按原频率 变化时, 有 1 C u i C (2) 由(1)和(2)式可求得 C 值: R C u C Ru (3) 实验中测量出 R u , C u 和给定的 R , 值,就可以求得i 和 C 的值
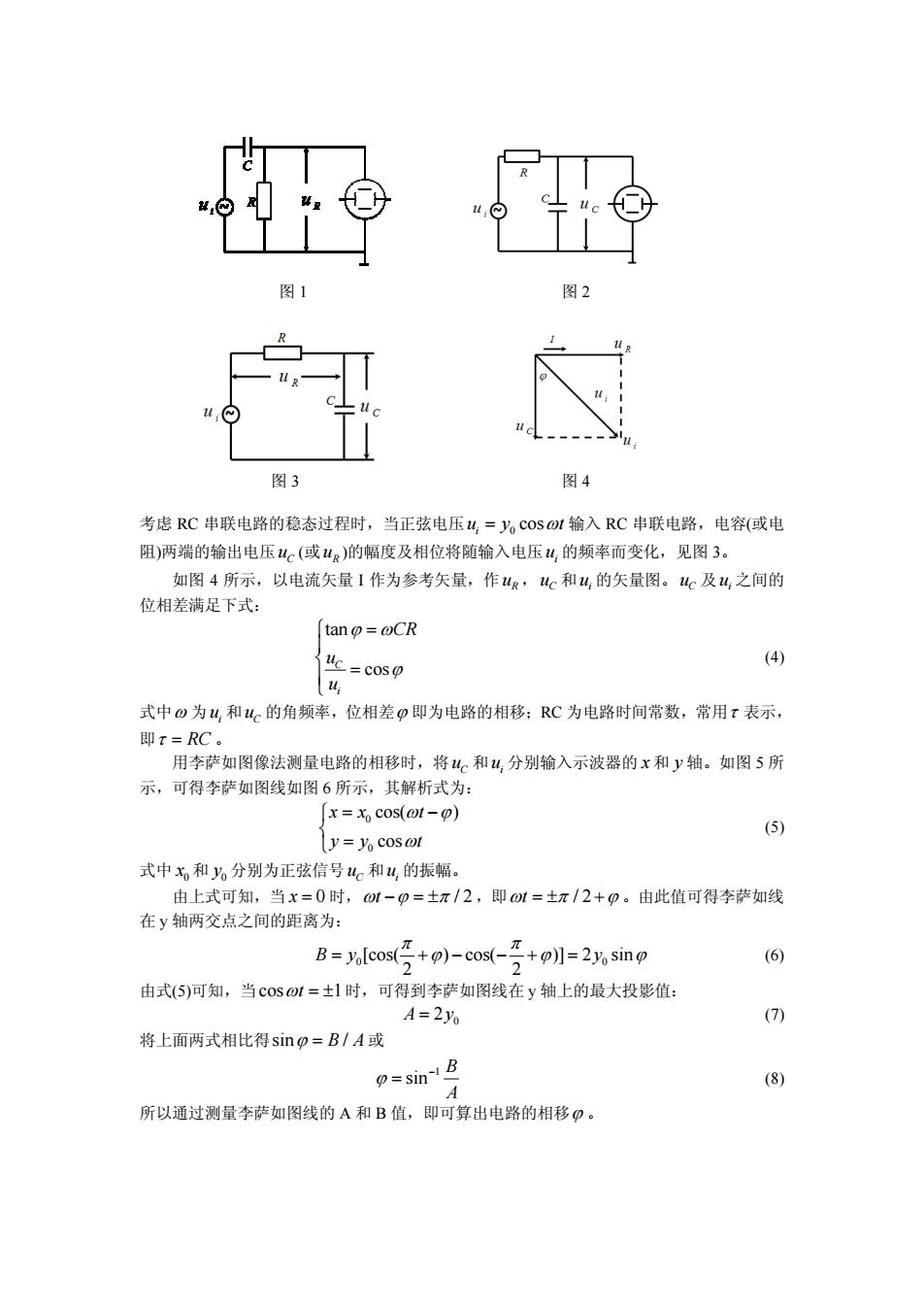
图4 考虑RC串联电路的稳态过程时,当正弦电压,=。cOS1输入RC串联电路,电容(或电 阻)两端的输出电压山(或w®)的幅度及相位将随输入电压私,的频率而变化,见图3。 如图4所示,以电流矢量I作为参考矢量,作ue,和弘,的矢量图。收及4,之间的 位相差满足下式: tan @CR (4) 式中0为4,和的角频率,位相差0即为电路的相移;RC为电路时间常数,常用r表示, 甲用如图像法测量电路的相移,将和分别铃入示波器的X和y销。如图5用 示,可得李萨如图线如图6所示,其解析式为: x=x cos(0I-0) (5) y=Vo cosof 式中x和⅓分别为正弦信号和4,的振幅。 由上式可知,当x=0时,1-p=±π/2,即1=土π/2+p。由此值可得李萨如线 在y轴两交点之间的距离为: B=yolcos()-cos(=2ysing 由式(5)可知,当cOs=±1时,可得到李萨如图线在y轴上的最大投影值: A=2 (7) 将上面两式相比得sinp=B/A或 =sin-1B (8) 所以通过测量李萨如图线的A和B值,即可算出电路的相移Q
图 1 图 2 图 3 图 4 考虑 RC 串联电路的稳态过程时,当正弦电压 0 cos i uy t 输入 RC 串联电路,电容(或电 阻)两端的输出电压 C u (或 R u )的幅度及相位将随输入电压 i u 的频率而变化,见图 3。 如图 4 所示,以电流矢量 I 作为参考矢量,作 R u , C u 和 i u 的矢量图。 C u 及 i u 之间的 位相差满足下式: tan cos C i CR u u (4) 式中 为 i u 和 C u 的角频率,位相差 即为电路的相移;RC 为电路时间常数,常用 表示, 即 RC 。 用李萨如图像法测量电路的相移时,将 C u 和 i u 分别输入示波器的 x 和 y 轴。如图 5 所 示,可得李萨如图线如图 6 所示,其解析式为: 0 0 cos( ) cos xx t yy t (5) 式中 0 x 和 0 y 分别为正弦信号 C u 和 i u 的振幅。 由上式可知,当 x 0 时,t / 2 ,即t / 2 。由此值可得李萨如线 在 y 轴两交点之间的距离为: 0 0 [cos( ) cos( )] 2 sin 2 2 By y (6) 由式(5)可知,当cos 1 t 时,可得到李萨如图线在 y 轴上的最大投影值: 0 A y 2 (7) 将上面两式相比得sin / B A 或 1 sin B A (8) 所以通过测量李萨如图线的 A 和 B 值,即可算出电路的相移

图5 2.RC串联电路实验数据举例 元件的标示值:R=20002,C=0.014F,测量值如表1所示: 1 f/x102h 4./×0.3 410.3 133.0 2.00 4.00 I0E00350004表号005048650 表 B1×0.31.501.701.902.052.202352.502.60 由表1得: c0sp=业=0.500 7=RC=an2=1.732/2mx13.0x102=207x10s 由表2可以导出表3 /x10e30035040045 50.055.0 60.065.0 tan 0.400.470.540.600.660.730.800.86 用最小二乘法得斜率 k=13.1×101E,=RC=2冬=208×10) 如果以后者为标准,则测量值的百分误差率为E=0.5%。 【实验仪 不同量值的电阻和电容、数字电压表、稳压电源、示波器、开关、秒表等 【设计要求】 用申压法训品充放申曲线 (1)电路参数的选择:根据实验室提供的仪器(秒表、电压表、电容),选择几组不 同的R,C值输入计算机,测试并描绘出一条充放电曲线,经过多次反复,得到一组符 合实验要求的电路参数R与C. (2)合理选择测量点的时间间隔:由于充放电过程中U)和I()随时间按指数规律变 化,它是一条非线性曲线。通过计算机模拟的曲线,合理设计时间间隔。 2用示波器观察输入方波时的暂态过程:在计算机上模拟不同的方波频率作用下,不 同电路参数时的充放电曲线。根据输出信号的要求,选择适当的参数输入计算机进行模
图 5 图 6 2.RC 串联电路实验数据举例 元件的标示值: R 2000 ,C F 0.01 ,测量值如表 1 所示: 表 1 2 f / 10 hz / 0.3 c u V / 0.3 i u V 133.0 2.00 4.00 表 2 (A=4.00*0.3V) 2 f / 10 hz 30.0 35.0 40.0 45.0 50.0 55.0 60.0 65.0 B / 0.3 V 1.50 1.70 1.90 2.05 2.20 2.35 2.50 2.60 由表 1 得: cos 0.500 C i u u 2 5 tan RC s 1.732 / 2 133.0 10 2.07 10 ( ) 由表 2 可以导出表 3 表 3 2 f / 10 hz 30.0 35.0 40.0 45.0 50.0 55.0 60.0 65.0 tan 0.40 0.47 0.54 0.60 0.66 0.73 0.80 0.86 用最小二乘法得斜率 5 k Hz 13.1 10 / , 5 2.08 10 ( ) 2 k RC s 如果以后者为标准,则测量值的百分误差率为 E 0.5% 。 【实验仪器】 各种不同量值的电阻和电容 、数字电压表、稳压电源、示波器、开关、秒表等。 【设计要求】 1.用电压法测量充放电曲线 (1)电路参数的选择:根据实验室提供的仪器(秒表、电压表、电容),选择几组不 同的 R,C 值输入计算机,测试并描绘出一条充放电曲线,经过多次反复,得到一组符 合实验要求的电路参数 R 与 C. (2)合理选择测量点的时间间隔:由于充放电过程中 Uc(t)和 I(t)随时间按指数规律变 化,它是一条非线性曲线。通过计算机模拟的曲线,合理设计时间间隔。 2.用示波器观察输入方波时的暂态过程:在计算机上模拟不同的方波频率作用下,不 同电路参数时的充放电曲线。根据输出信号的要求,选择适当的参数输入计算机进行模

拟,直至选出最佳的参数。 【问题与讨论】 分析实验误差产生的原因。 【注意事项】 1电解电容应分清正负极。充电时,不能将电源正负极接反,不能超过其耐压范围。 2预习报告要求:a.写出实验原理和计算公式;b拟出实验步骤;c列出数据表格:d 列出所需仪器清单(注明型号规格)
拟,直至选出最佳的参数。 【问题与讨论】 分析实验误差产生的原因。 【注意事项】 1.电解电容应分清正负极。充电时,不能将电源正负极接反,不能超过其耐压范围。 2.预习报告要求:a.写出实验原理和计算公式;b.拟出实验步骤;c.列出数据表格;d. 列出所需仪器清单(注明型号规格)