
第3章事故树分析法 Accident Tree Analysis
1 第3章 事故树分析法 Accident Tree Analysis

本章内容及大纲 3.1事故树的发展历史 3.2基本概念 3.3事故树分析方法的步骤 3.4事故树的符号及其意义 3.5事故树的编制和用途 3.6布尔代数与主要运算法则 3.7利用布尔代数化简事故树 3.8最小割集的概念和求法 3.9最小径集的概念和求法 3.10基本事件的结构重要度分析
2 本章内容及大纲 3.1 事故树的发展历史 3.2 基本概念 3.3 事故树分析方法的步骤 3.4 事故树的符号及其意义 3.5 事故树的编制和用途 3.6 布尔代数与主要运算法则 3.7 利用布尔代数化简事故树 3.8 最小割集的概念和求法 3.9 最小径集的概念和求法 3.10 基本事件的结构重要度分析

3.1 事故树的发展历史 ·事故树分析(Fault Tree Analysis或Accident Tree Analysis),缩 写为FTA或ATA。 ●1961年美国贝尔电话研究所的沃森(H.A.Watson)在研究民兵式导 弹发射控制系统的安全性评价时,首先提出了这个方法; ● 接着该所的默恩斯(A.B.Mearns)等人改进了这个方法,对解决 火箭偶发事故的预测问题作出了贡献。 ●其后,美国波音飞机公司的哈斯尔Hassl)等人对这个方法又作了重 大改进,并采用计算机进行辅助分析和计算。 。1974年美国原子能委员会应用FTA对商用核电站的灾害危险性进行 评价,发表了拉斯马森报告(Rasmussen Report),引起了世界各 国的关注
3 3.1 事故树的发展历史 ⚫ 事故树分析(Fault Tree Analysis或Accident Tree Analysis ),缩 写为FTA或ATA。 ⚫ 1961年美国贝尔电话研究所的沃森(H.A.Watson)在研究民兵式导 弹发射控制系统的安全性评价时,首先提出了这个方法; ⚫ 接着该所的默恩斯(A. B. Mearns)等人改进了这个方法,对解决 火箭偶发事故的预测问题作出了贡献。 ⚫ 其后,美国波音飞机公司的哈斯尔(Hassl)等人对这个方法又作了重 大改进,并采用计算机进行辅助分析和计算。 ⚫ 1974年美国原子能委员会应用FTA对商用核电站的灾害危险性进行 评价,发表了拉斯马森报告(Rasmussen Report),引起了世界各 国的关注

3.1 事故树的发展历史 ·1976年,清华大学核能技术研究所在核反应堆的安全评价中开始应 用了FTA。 ·1978年,天津东方红化工厂首次用FTA控制生产中的事故,获得成 功。 1982年,在北京市劳动保护研究所,召开了第一次安全系统工程座 ● 谈会,介绍和推广了FTA。 ●实践证明,FTA是一种具有广阔的应用范围和发展前途的系统安全分 析方法
4 3.1 事故树的发展历史 ⚫ 1976年,清华大学核能技术研究所在核反应堆的安全评价中开始应 用了FTA。 ⚫ 1978年,天津东方红化工厂首次用FTA控制生产中的事故,获得成 功。 ⚫ 1982年,在北京市劳动保护研究所,召开了第一次安全系统工程座 谈会,介绍和推广了FTA。 ⚫ 实践证明,FTA是一种具有广阔的应用范围和发展前途的系统安全分 析方法
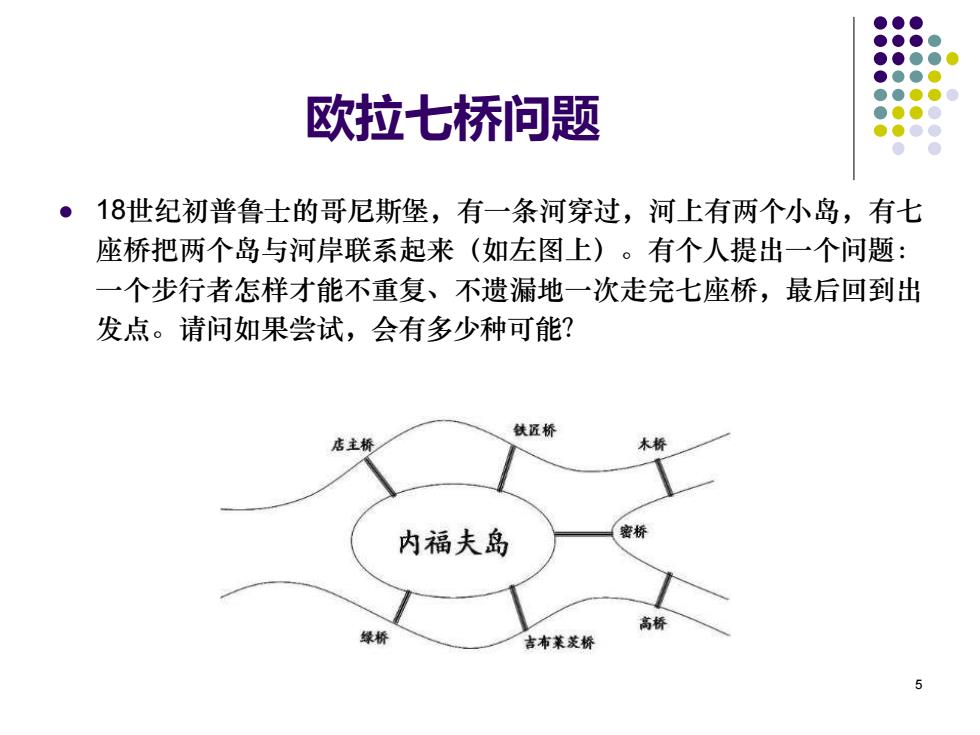
欧拉七桥问题 ●18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七 座桥把两个岛与河岸联系起来(如左图上)。有个人提出一个问题: 一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出 发点。请问如果尝试,会有多少种可能? 铁匠桥 店主桥 木桥 内福夫岛 密桥 高桥 绿桥 吉布莱茨桥
欧拉七桥问题 ⚫ 18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七 座桥把两个岛与河岸联系起来(如左图上)。有个人提出一个问题: 一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出 发点。请问如果尝试,会有多少种可能? 5

欧拉七桥问题 后来大数学家欧拉把它转化成一个几何问题一一笔画问题。他不仅解决了此问 题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0个就是2个 (连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一 笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两 端,因此任何图能一笔画成,奇点要么没有要么在两端)。因此,7桥问题无解
欧拉七桥问题 6 后来大数学家欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问 题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0 个就是2 个 (连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一 笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两 端,因此任何图能一笔画成,奇点要么没有要么在两端)。因此,7桥问题无解
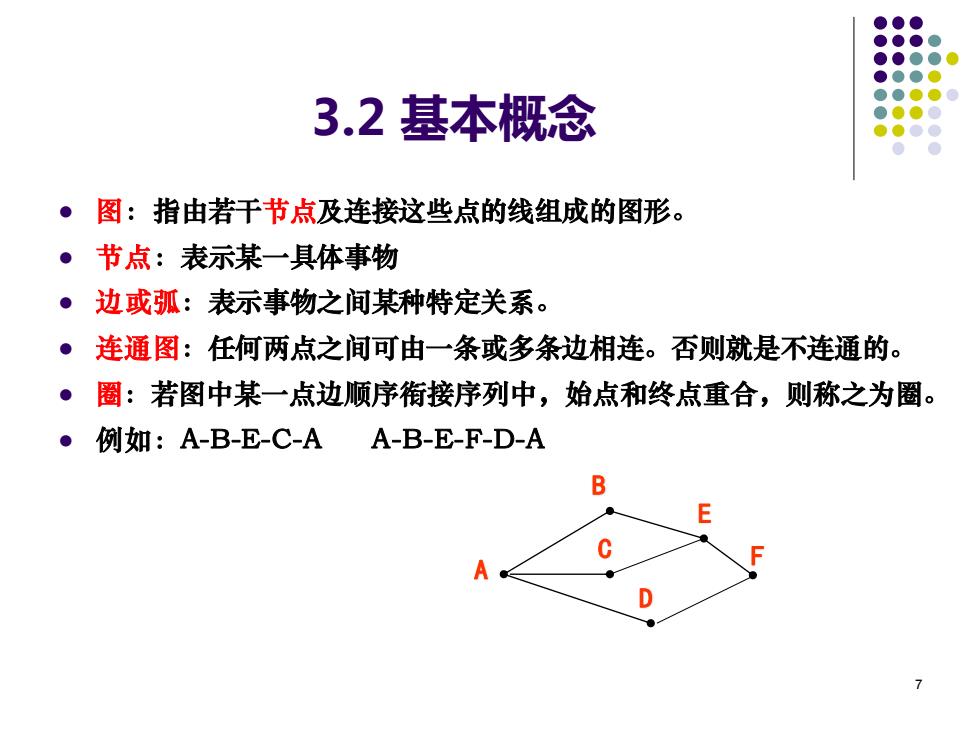
3.2基本概念 ·图:指由若干节点及连接这些点的线组成的图形。 。节点:表示某一具体事物 。边或弧:表示事物之间某种特定关系。 ·连通图:任何两点之间可由一条或多条边相连。否则就是不连通的。 ·圈:若图中某一点边顺序衔接序列中,始点和终点重合,则称之为圈。 。1 例如:A-B-E-C-A A-B-E-F-D-A B E A D
7 3.2 基本概念 ⚫ 图:指由若干节点及连接这些点的线组成的图形。 ⚫ 节点:表示某一具体事物 ⚫ 边或弧:表示事物之间某种特定关系。 ⚫ 连通图:任何两点之间可由一条或多条边相连。否则就是不连通的。 ⚫ 圈:若图中某一点边顺序衔接序列中,始点和终点重合,则称之为圈。 ⚫ 例如:A-B-E-C-A A-B-E-F-D-A B A C D E F
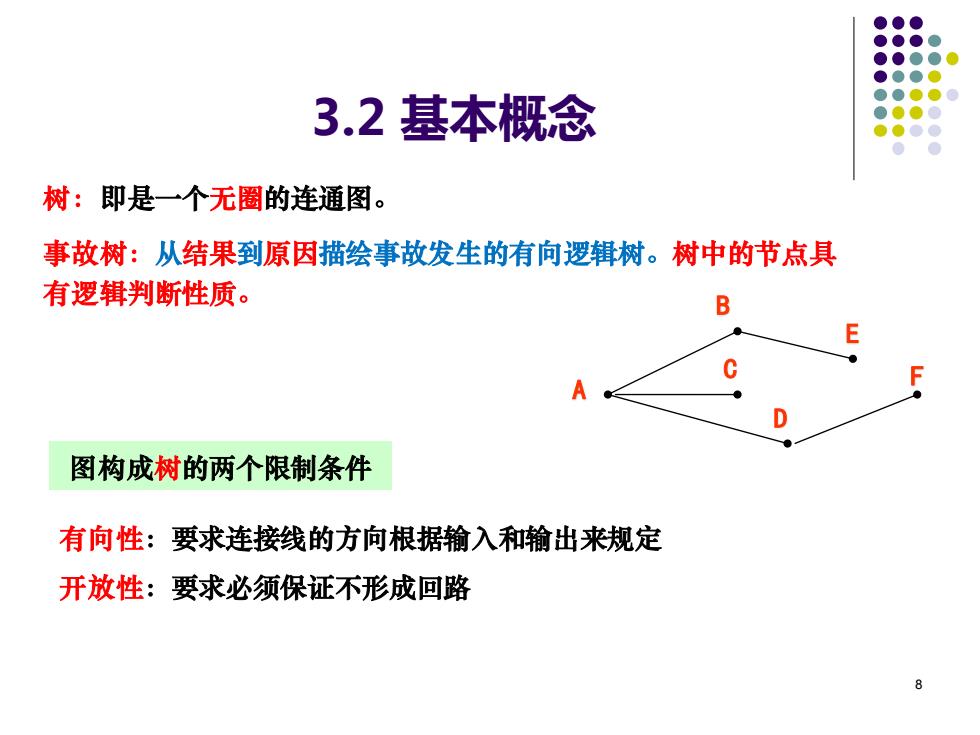
3.2基本概念 树:即是一个无圈的连通图。 事故树:从结果到原因描绘事故发生的有向逻辑树。树中的节点具 有逻辑判断性质。 B E 图构成树的两个限制条件 有向性:要求连接线的方向根据输入和输出来规定 开放性:要求必须保证不形成回路
8 3.2 基本概念 树:即是一个无圈的连通图。 事故树:从结果到原因描绘事故发生的有向逻辑树。树中的节点具 有逻辑判断性质。 B A C D E F 图构成树的两个限制条件 有向性:要求连接线的方向根据输入和输出来规定 开放性:要求必须保证不形成回路

事故树的概念 ·形似倒立着的树。 ●树的“根部”顶点节点表示系统的某一个事故, ●树的“梢”底部节点表示事故发生的基本原因, ●树的“枝权”中间节点表示由基本原因促成的事故结果,又是系统事 故的中间原因; ●事故因果关系的不同性质用不同的逻辑门表示。 这样画成的一个“树”用来描述某种事故发生的因果关系,称之为事 故树
9 事故树的概念 ⚫ 形似倒立着的树。 ⚫ 树的“根部”顶点节点表示系统的某一个事故, ⚫ 树的“梢”底部节点表示事故发生的基本原因, ⚫ 树的“枝杈”中间节点表示由基本原因促成的事故结果,又是系统事 故的中间原因; ⚫ 事故因果关系的不同性质用不同的逻辑门表示。 ⚫ 这样画成的一个“树”用来描述某种事故发生的因果关系,称之为事 故树

3.3事故树分析方法的步骤 ·事故树分析是根据系统可能发生的事故或已经发生的事故所提供的信 息,去寻找同类事故发生有关的原因,从而采取有效的防范措施,防 止同类事故再次发生。 ·事故树分析的主要步骤包括: 。3.3.1编制事故树 ·3.3.2事故树定性分析 ·3.3.3事故树定量分析 ●3.3.4制定预防事故和改进系统的措施 10
10 3.3 事故树分析方法的步骤 ⚫ 事故树分析是根据系统可能发生的事故或已经发生的事故所提供的信 息,去寻找同类事故发生有关的原因,从而采取有效的防范措施,防 止同类事故再次发生。 ⚫ 事故树分析的主要步骤包括: ⚫ 3.3.1 编制事故树 ⚫ 3.3.2 事故树定性分析 ⚫ 3.3.3 事故树定量分析 ⚫ 3.3.4 制定预防事故和改进系统的措施