
第4章 工程风险的估计
1 第4章 工程风险的估计

本章内容及大纲 ·第1节工程风险估计概述 ●第2节工程风险估计的方法 ●第3节工程风险损失的内容 ●第4节工程风险估计的应用 ·第5节工程风险损失影响程度的度量方法
2 本章内容及大纲 ⚫ 第1节 工程风险估计概述 ⚫ 第2节 工程风险估计的方法 ⚫ 第3节 工程风险损失的内容 ⚫ 第4节 工程风险估计的应用 ⚫ 第5节 工程风险损失影响程度的度量方法

第1节 工程风险估计概述
3 第1节 工程风险估计概述

1.工程风险估计的内涵 ●工程风险估计是建立在有效识别工程风险的基础上,根据 工程风险的特点,对已经确认的风险,通过定性和定量方 法估计其发生的可能性和破坏程度的大小。 ·工程风险估计对风险按潜在危险大小进行优先排序和评价、 制定风险对策和选择风险应对方案有重要的作用。 ·工程风险通常采用统计法、分析法和推断法,一般需要一 些列可信的历史资料数据和相关数据以及足以说明被估计 对象的特性和状态的数据做保证。当资料不全时往往依靠 主管推断来弥补
4 1. 工程风险估计的内涵 ⚫ 工程风险估计是建立在有效识别工程风险的基础上,根据 工程风险的特点,对已经确认的风险,通过定性和定量方 法估计其发生的可能性和破坏程度的大小。 ⚫ 工程风险估计对风险按潜在危险大小进行优先排序和评价、 制定风险对策和选择风险应对方案有重要的作用。 ⚫ 工程风险通常采用统计法、分析法和推断法,一般需要一 些列可信的历史资料数据和相关数据以及足以说明被估计 对象的特性和状态的数据做保证。当资料不全时往往依靠 主管推断来弥补

2.工程风险估计的作用 ·有助于管理者加深对工程项目自身所处环境的理解,为进 一步制定工程项目实施方案提供可靠信息。 ·有利于明确不确定性因素对工程各方面产生的影响。决策 者可以通过对风险估计发生概率高或者对工程项目影响程 度大的风险因素制定应对措施,将潜在风险损失降到最低 程度或者可接受程度。 ·为分析整个工程风险或某一类风险发生的概率提供依据, 并可以作为风险评价、确定应对措施和进行监控的基础。 管理者可以结合损失程度的估计结果分配风险管理费用
5 2. 工程风险估计的作用 ⚫ 有助于管理者加深对工程项目自身所处环境的理解,为进 一步制定工程项目实施方案提供可靠信息。 ⚫ 有利于明确不确定性因素对工程各方面产生的影响。决策 者可以通过对风险估计发生概率高或者对工程项目影响程 度大的风险因素制定应对措施,将潜在风险损失降到最低 程度或者可接受程度。 ⚫ 为分析整个工程风险或某一类风险发生的概率提供依据, 并可以作为风险评价、确定应对措施和进行监控的基础。 管理者可以结合损失程度的估计结果分配风险管理费用
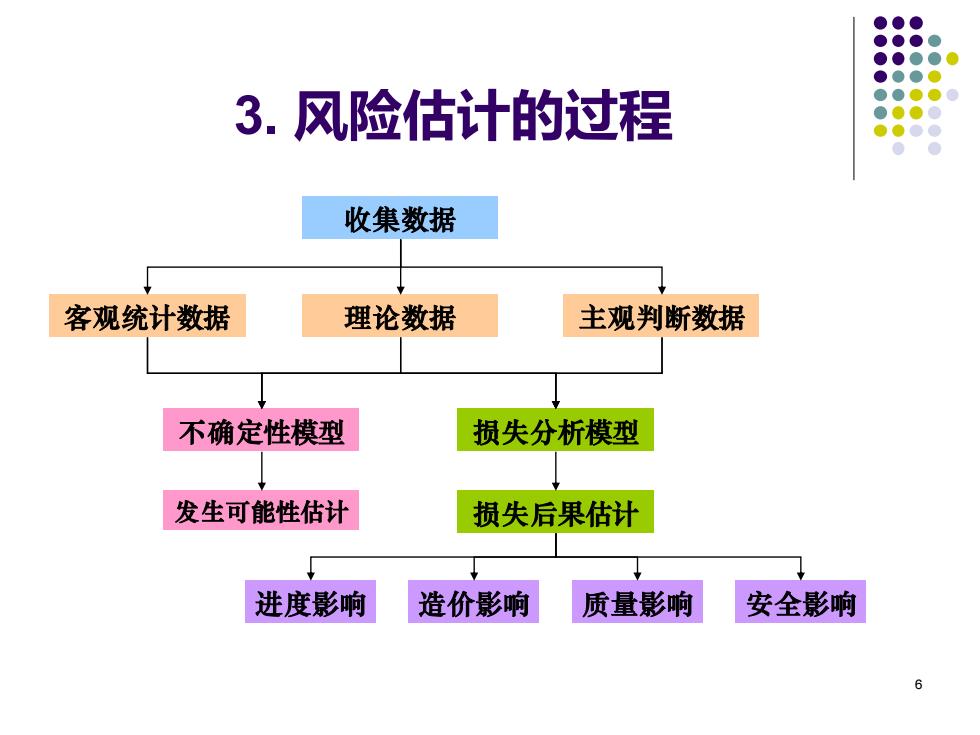
3.风险估计的过程 收集数据 客观统计数据 理论数据 主观判断数据 不确定性模型 损失分析模型 发生可能性估计 损失后果估计 进度影响 造价影响 质量影响 安全影响
6 3. 风险估计的过程 收集数据 客观统计数据 理论数据 主观判断数据 不确定性模型 损失分析模型 发生可能性估计 损失后果估计 进度影响 造价影响 质量影响 安全影响

4.工程风险估计的内容 ·①风险事件发生的可能性估计 ●②风险事件后果严重程度估计 ●③风险事件影响范围的估计 ●④风险事件发生时间的估计
7 4. 工程风险估计的内容 ⚫ ① 风险事件发生的可能性估计 ⚫ ② 风险事件后果严重程度估计 ⚫ ③ 风险事件影响范围的估计 ⚫ ④ 风险事件发生时间的估计

5.风险估计的理论基础 ●5.1大数定律 ●5.2概率推断的原理 ●5.3类推原理 ●5.4惯性原理
8 5. 风险估计的理论基础 ⚫ 5.1 大数定律 ⚫ 5.2 概率推断的原理 ⚫ 5.3 类推原理 ⚫ 5.4 惯性原理

5.1大数定律 。大数定律(Law of Large Numbers),又称大数定理,是 一种描述当试验次数很大时所呈现的概率性质的定律。但 是注意到,虽然通常最常见的称呼是大数“定律”,但是 大数定律并不是经验规律,而是严格证明了的定理。 。有些随机事件无规律可循,但不少是有规律的,这些“有 规律的随机事件”在大量重复出现的条件下,往往呈现几 乎必然的统计特性,这个规律就是大数定律。 确切的说大数定律是以确切的数学形式表达了大量重复出 现的随机现象的统计规律性,即频率的稳定性和平均结果 的稳定性,并讨论了它们成立的条件
9 5.1 大数定律 ⚫ 大数定律(Law of Large Numbers),又称大数定理,是 一种描述当试验次数很大时所呈现的概率性质的定律。但 是注意到,虽然通常最常见的称呼是大数“定律” ,但是 大数定律并不是经验规律,而是严格证明了的定理。 ⚫ 有些随机事件无规律可循,但不少是有规律的,这些“有 规律的随机事件”在大量重复出现的条件下,往往呈现几 乎必然的统计特性,这个规律就是大数定律。 ⚫ 确切的说大数定律是以确切的数学形式表达了大量重复出 现的随机现象的统计规律性,即频率的稳定性和平均结果 的稳定性,并讨论了它们成立的条件

① 切比雪夫大数定律 设:x,2,.x是一列两两相互独立的随机变量且服从同一分布, 且存在有限的数学期望a和方差σ2,则对任意小的正数8,满足以下 公式: 2 lim 1→00 该定律的含义是:当很大,服从同一分布的随机变量的算术平均数将依 概率接近于这些随机变量的数学期望。 将该定律应用于抽样调查,就会有如下结论:随着样本容量的增加,样 本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计 总体平均数提供了理论依据。 10
10 ① 切比雪夫大数定律 公式: 且存在有限的数学期望 和方差 ,则对任意小的正数 ,满足以下 设: 是一列两两相互独立的随机变量且服从同一分布, 2 1 2 , , a x x x n lim ( − ) =1 → a n x P i n 该定律的含义是:当n很大,服从同一分布的随机变量的算术平均数将依 概率接近于这些随机变量的数学期望。 将该定律应用于抽样调查,就会有如下结论:随着样本容量n的增加,样 本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计 总体平均数提供了理论依据