
同海才 TONGJI UNIV →1 ninput x2- Z2 m output variables variables Xn Zm Combinational circut y1 Y k secondary k excitation variables y2 Y variables (present (next state) state) yk Yk Delay Delay Delay 2002 Prentice Hall.Inc. M.Morris Mano Fig.9-1 Block Diagram of an Asynchronous Sequential Circuit DIGITAL DESIGN,3e

同桥大学 TONGJI UNIVERSITY How to analyze a asynchronous circuit? ● Check the feedback. o Do it in the combinational circuit way. ● Establish the state transition table
How to analyze a asynchronous circuit? ⚫Check the feedback. ⚫Do it in the combinational circuit way. ⚫Establish the state transition table
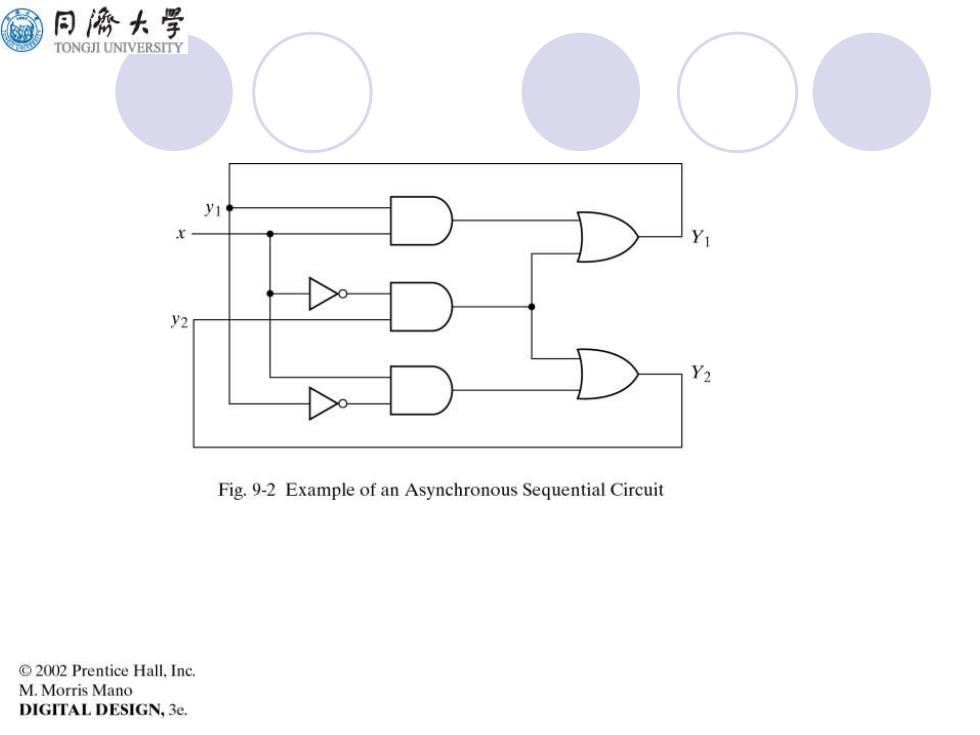
同海大学 TONGJI UNIVERSITY Fig.9-2 Example of an Asynchronous Sequential Circuit 2002 Prentice Hall.Inc. M.Morris Mano DIGITAL DESIGN,3e
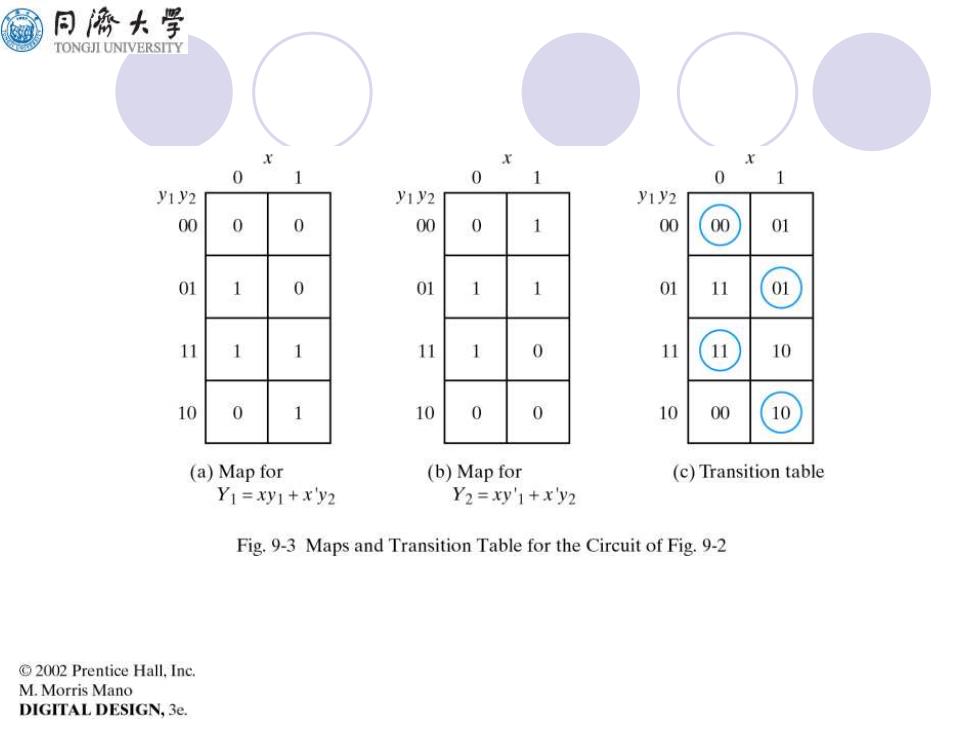
同海大学 TONGJI UNIVERSITY 0 0 y1y2 y1y2 yiy2 00 0 0 00 0 00 00 01 1 0 01 1 1 01 11 01 11 1 1 11 0 11 11 10 10 0 10 0 0 10 00 10 (a)Map for (b)Map for (c)Transition table Y1=xy1+xy2 Y2=xy1+xy2 Fig.9-3 Maps and Transition Table for the Circuit of Fig.9-2 2002 Prentice Hall,Inc. M.Morris Mano DIGITAL DESIGN,3e

同桥大学 TONGJI UNIVERSITY Stable and unstable states The circle indicate the stable state. OUn-circled states are not stable,which means state transition could take place o The state transition will continue until the system reaches a stable state
Stable and unstable states ⚫The circle indicate the stable state. ⚫Un-circled states are not stable, which means state transition could take place ⚫The state transition will continue until the system reaches a stable state
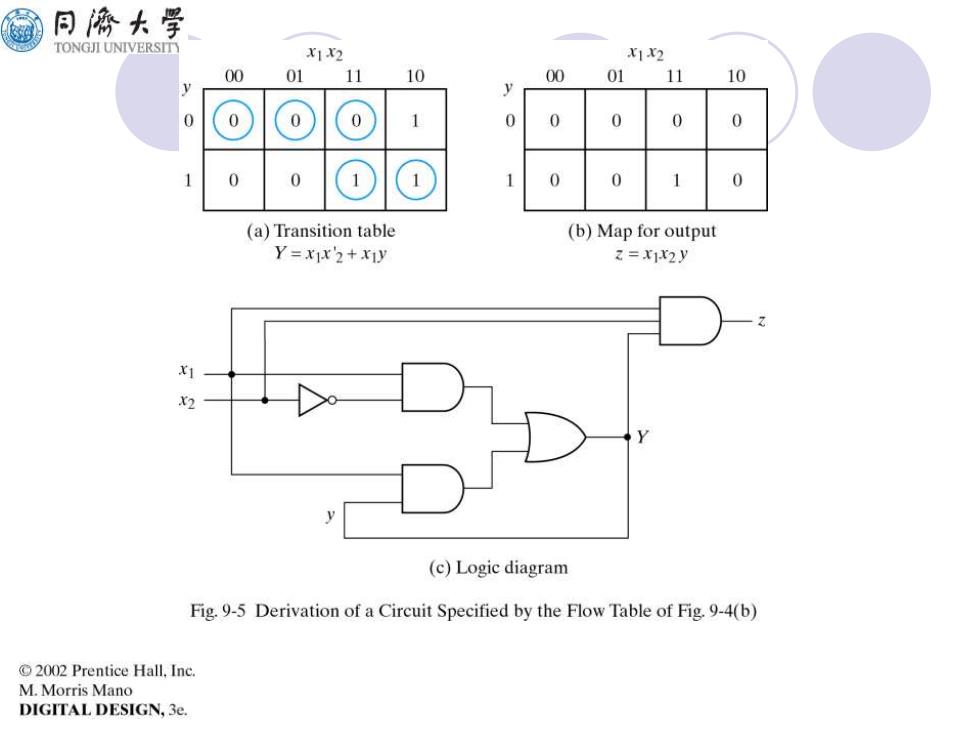
同海大学 TONGJI UNIVERSITY X1X2 X1X2 00 01 11 10 00 01 1 10 0 0 0 0 0 0 0 0 0 0 (a)Transition table (b)Map for output Y=xx2+xiy Z=x1xy X2 (c)Logic diagram Fig.9-5 Derivation of a Circuit Specified by the Flow Table of Fig.9-4(b) 2002 Prentice Hall.Inc. M.Morris Mano DIGITAL DESIGN,3e

同©大学 TONGJI UNIVERSITY ● o Represent the states with alphabets
⚫Represent the states with alphabets

同榜大学 TONGJI UNIVERSITY Circuit instability (cycles) oWhen the state transition takes all the time, the circuit will not fall in one stable state, we call the circuit is not stable
Circuit instability (cycles) ⚫When the state transition takes all the time, the circuit will not fall in one stable state, we call the circuit is not stable
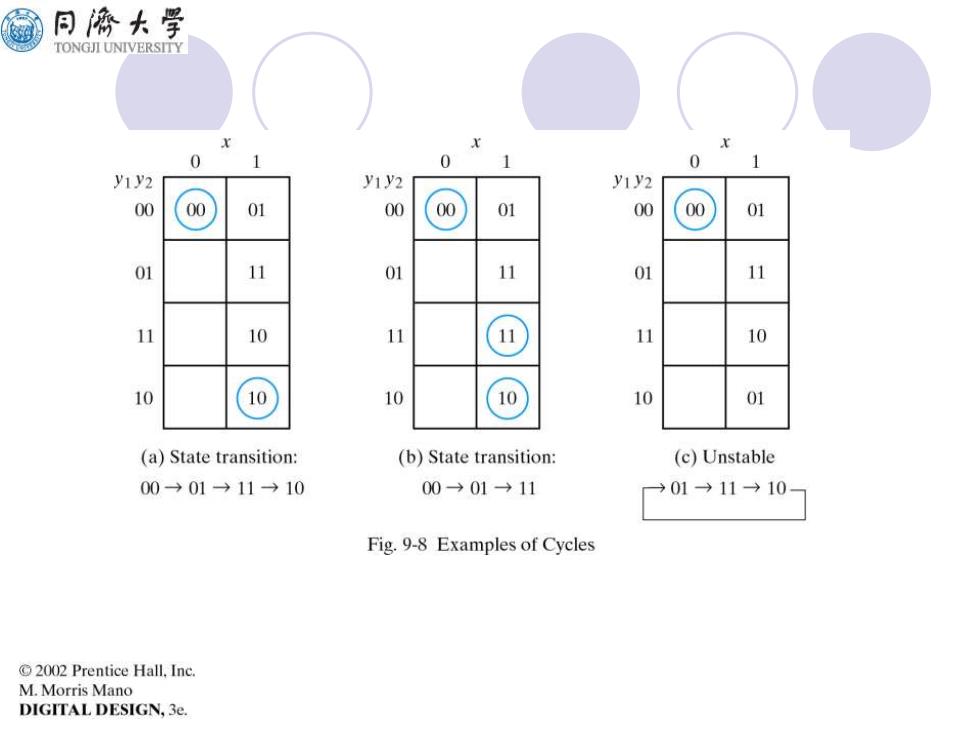
同桥大学 TONGJI UNIVERSITY 0 0 y1y2 y1y2 y1y2 00 00 2 00 00 01 00 00 01 01 11 01 11 01 11 10 11 11 11 10 10 10 10 10 10 01 (a)State transition: (b)State transition: (c)Unstable 00→01→11→10 00→01→11 )01→11→10 Fig.9-8 Examples of Cycles 2002 Prentice Hall.Inc. M.Morris Mano DIGITAL DESIGN,3e

同桥大学 TONGJI UNIVERSITY (a)Logic diagram X1x2 00 01 10 0 0 0 0 0 (b)Transition table Fig.9-9 Example of an Unstable Circuit 2002 Prentice Hall,Inc. M.Morris Mano DIGITAL DESIGN,3e