
数字电路总复习
数字电路总复习

第一、二章逻辑代数基础 1、数制的转换 二进制→十进制 例如:(1101.01)2=1×23+1×22+0×21+ 1X20+0X21+1×22=(13.25) 10 十进制→二进制 整数部分的转换: 将十进制数除2,得到的余数即为k,然后将其 商除2,余数为k1’.依次求得k2,kn,直 至商为0
1、数制的转换 二进制 十进制 例如:(1101.01)2=1×2 3+ 1×2 2+ 0×2 1+ 1×2 0+ 0×2 -1+ 1×2 -2=(13.25)10 十进制 二进制 整数部分的转换: 将十进制数除2,得到的余数即为k0 ,然后将其 商除2,余数为k1,.依次求得k2,.kn,直 至商为0。 第一、二章 逻辑代数基础

小数部分的转换: 将十进制数乘以2,得到的整数部分即 为k1,然后再将其小数部分乘以2,所得整 数部分为k2,依次求得k2,···,K, 直至小数部分为0
小数部分的转换: 将十进制数乘以2,得到的整数部分即 为k-1 ,然后再将其小数部分乘以2,所得整 数部分为k-2,依次求得k-2 , ...,K-m, 直至小数部分为0

二进制之 十六进制 (00010110.01101100)2=(16.6C)16 (3A.B8)16=(00111010.10111000)2 常用的十进制代码: ·8421(BCD)码 ·余3码
(0001 0110.0110 1100) 2 =(16.6C)16 (3A.B8)16=(0011 1010.10111000)2 二进制 十六进制 常用的十进制代码: • 8421(BCD)码 • 余3码

2、带符号的二进制数的原码、反码、补码: 原码: 正数符号位0+数值; 负数 符号位1+数值; 反码: 正数同原码; 负数 符号位1+数值逐位求反; 补码 正数同原码; 负数 反码+1;
原码: 正数 符号位 0+数值; 负数 符号位 1+数值; 反码: 正数 同原码; 负数 符号位 1+数值逐位求反; 补码 正数 同原码; 负数 反码+1; 2、带符号的二进制数的原码、反码、补码:

3、逻辑代数的基本公式和常用公式 基本公式 0-1律:0A=0,0+A=A,1·A=A,1+A=1 重叠律:A·A=A,A+A=A,AA=0,A+A=1 交换律:AB=BA, A+B-B+A 结合律:A(BC)=(AB)·C,A+(B+C)=(A+B)+C 分配律:A·B+C)=AB+A·C A+B.C=(A+B)(A+C) 反演律: AB=A+B A+B=A·B 还原律: A=A,1=0, 0=1
基本公式 还原律: A=A , 1=0 , 0=1 0—1律: 0·A=0, 0+A=A, 1 · A=A, 1+A=1 重叠律: A ·A=A , A+A=A , A·A=0 , A+A=1 交换律:A·B=B·A , A+B=B+A 结合律:A·(B·C)=(A·B) ·C , A+(B+C)=(A+B)+C 分配律:A· (B+C)=A·B+A·C A+B·C=(A+B) ·(A+C) 反演律: A·B=A+B , A+B = A·B 3、逻辑代数的基本公式和常用公式

常用公式 A+A·B=A A+A·B=A+B AB+AB=A A·(A+B)=A AB+AC+BC=AB+AC AB+A·C+BCD=A·B+A·C A·AB=A·B AAB=A
A+A·B=A A+A·B=A+B A·B+A·B=A A·(A+B)=A A·B+A·C+B·C=A·B+A·C A·B+A·C+BCD=A·B+A·C A·A·B=A·B A·AB=A 常用公式

4、逻辑函数的表示方法 1) 逻辑真值表 2)逻辑函数式 相互转换 3)逻辑图 4)卡诺图
1)逻辑真值表 2)逻辑函数式 3)逻辑图 4)卡诺图 相互转换 4、逻辑函数的表示方法
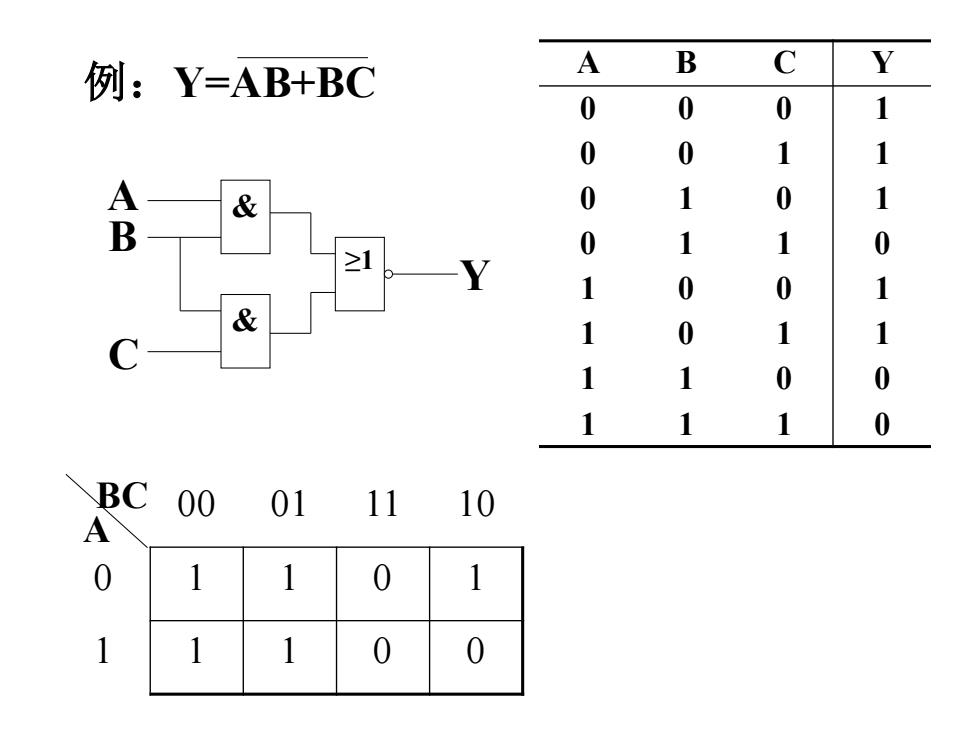
例:Y=AB+BC A B Y 0 0 0 1 0 0 1 1 A & 0 1 0 1 B 0 1 1 0 Y 1 0 0 1 & 1 0 1 1 C 1 1 0 0 1 1 1 0 BC 00 01 11 10 A 0 1 1 0 1 1 1 1 0 0
例:Y=AB+BC && ≥1 ABC Y A B C Y 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 00 01 11 10 0 1 1 0 1 1 1 1 0 0 A BC
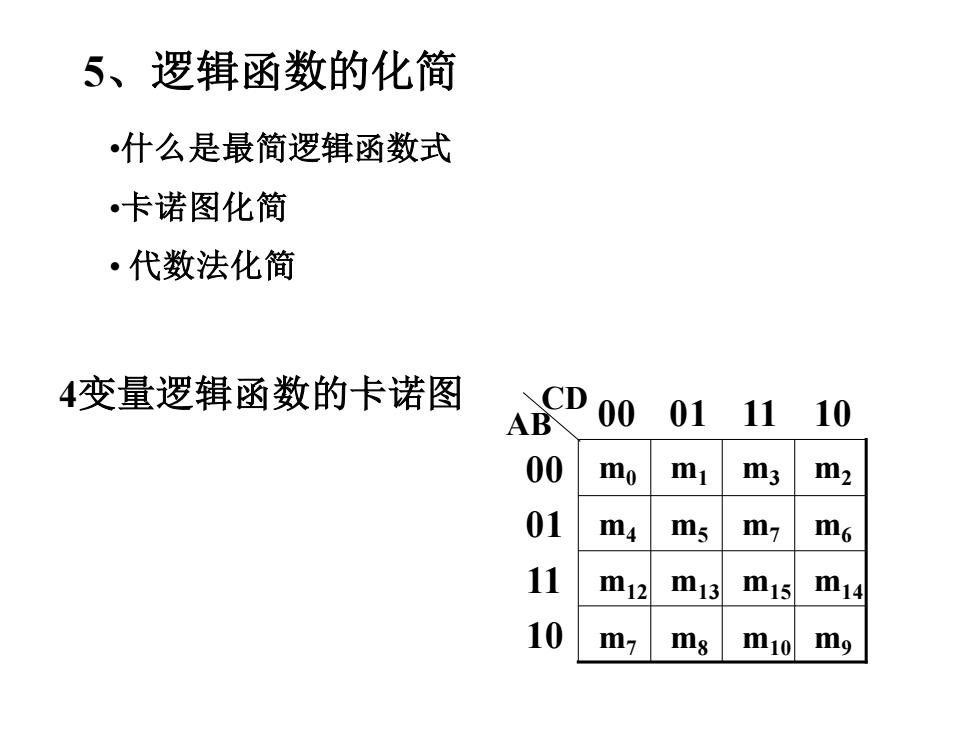
5、逻辑函数的化简 •什么是最简逻辑函数式 。卡诺图化简 ·代数法化简 4变量逻辑函数的卡诺图 CD 00 AB 0111 10 00 mo mi m3 m2 01 m m5 m7 m6 11 m12 m13 m15 m14 10 m7 ms mi0m9
•什么是最简逻辑函数式 •卡诺图化简 • 代数法化简 4变量逻辑函数的卡诺图 10 11 01 00 AB 00 01 11 10 CD m0 m1 m4 m5 m3 m2 m7 m6 m12 m13 m7 m8 m15 m14 m10 m9 5、逻辑函数的化简