
第四章组合逻辑电路的设计 •常用组合逻辑模块 •组合逻辑电路的分析方法和设计方法 组合逻辑电路的竞争冒险现象
第四章 组合逻辑电路的设计 •常用组合逻辑模块 •组合逻辑电路的分析方法和设计方法 •组合逻辑电路的 竞争冒险现象

4.1组合逻辑电路的分析方法 组合逻辑电路 逻辑电路 时序逻辑电路 组合逻辑电路的特点: 任意时刻的输出仅仅取决于该时刻 的输入,与电路的原来状态无关
4.1 组合逻辑电路的分析方法 组合逻辑电路 逻辑电路 时序逻辑电路 组合逻辑电路的特点: 任意时刻的输出仅仅取决于该时刻 的输入,与电路的原来状态无关
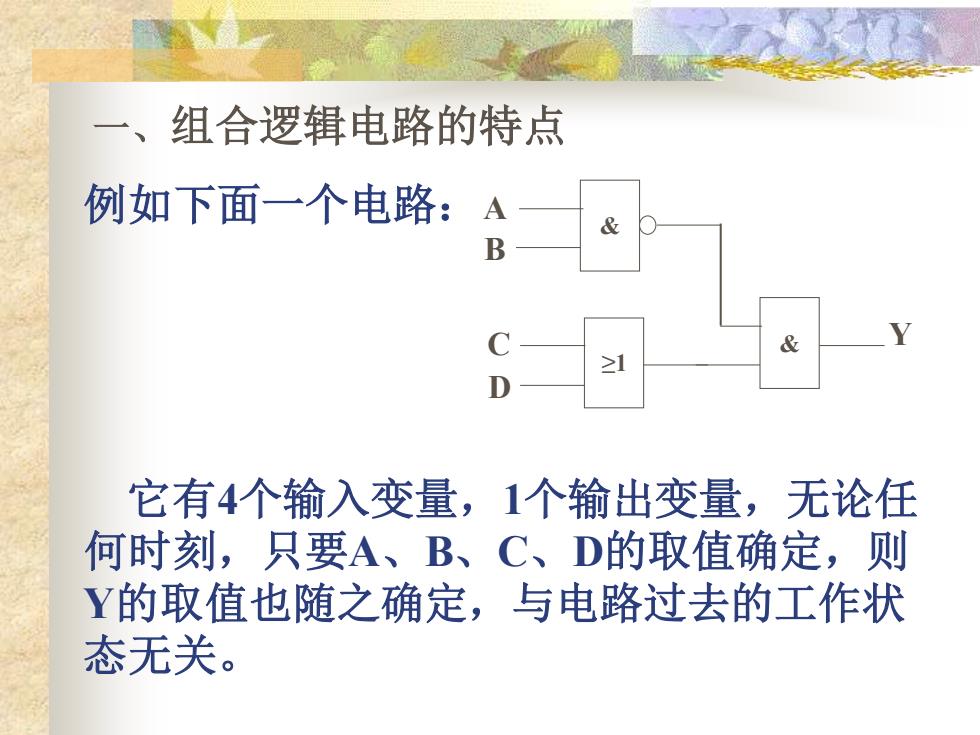
一、 组合逻辑电路的特点 例如下面一个电路:A & B C ≥1 D 它有4个输入变量,1个输出变量,无论任 何时刻,只要A、B、C、D的取值确定,则 Y的取值也随之确定,与电路过去的工作状 态无关
一、组合逻辑电路的特点 例如下面一个电路: & A B ≥1 C & Y D 它有4个输入变量,1个输出变量,无论任 何时刻,只要A、B、C、D的取值确定,则 Y的取值也随之确定,与电路过去的工作状 态无关

二、组合逻辑电路的分析 组合逻辑电路的分析 找出逻辑电路的逻辑功能。 (逻辑电路→逻辑功能)
二、组合逻辑电路的分析 组合逻辑电路的分析 —找出逻辑电路的逻 辑功能。 (逻辑电路 逻辑功能)

分析的方法: a.从电路的输入到输出逐级写出逻辑函 数式,最后得到输出与输入关系的逻辑函数 式。 b.用公式法或卡诺图法对得到的函数式 化简或变换,使逻辑关系简单明了。 c.为了使电路的逻辑功能更加直观,有 时还需把逻辑函数式转换为真值表的形式。 电路图→函数式→化简→真值表(逻辑功能)
a. 从电路的输入到输出逐级写出逻辑函 数式,最后得到输出与输入关系的逻辑函数 式。 b. 用公式法或卡诺图法对得到的函数式 化简或变换,使逻辑关系简单明了。 c. 为了使电路的逻辑功能更加直观,有 时还需把逻辑函数式转换为真值表的形式。 电路图 函数式 化简 真值表(逻辑功能) 分析的方法:
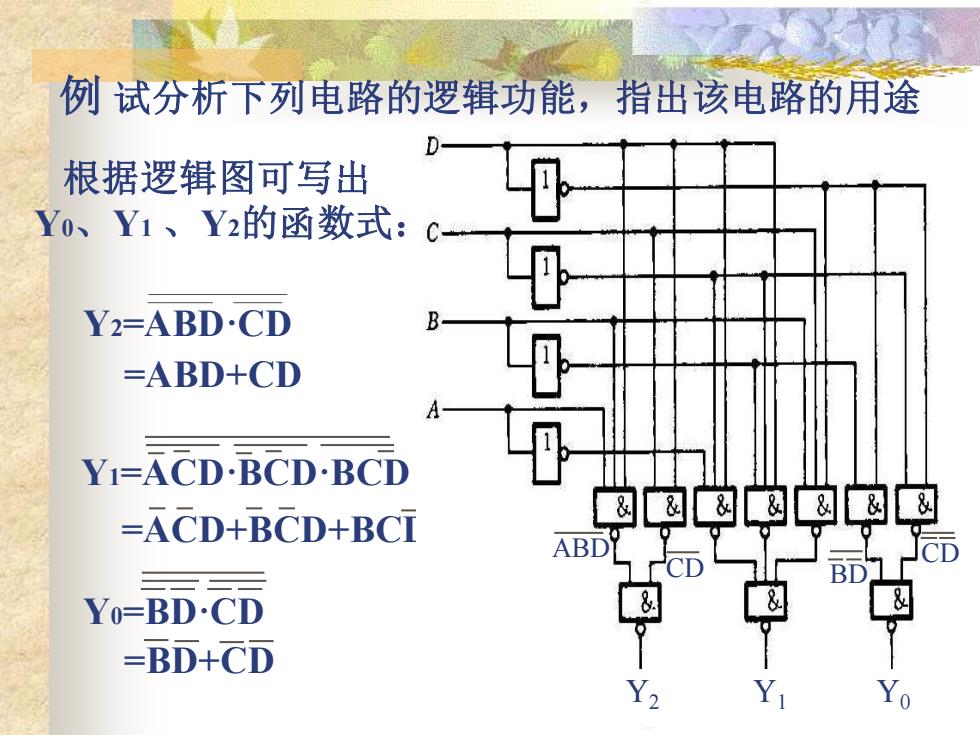
例试分析下列电路的逻辑功能,指出该电路的用途 根据逻辑图可写出 Yo、Y1、Y2的函数式: C Y2=ABD·CD =ABD+CD Y1=ACD·BCDBCD =ACD+BCD+BCI ABDY CD Yo=BD·CD =BD+CD
Y2=ABD·CD =ABD+CD =ACD+BCD+BCD Y1=ACD·BCD·BCD Y0=BD·CD =BD+CD 根据逻辑图可写出 Y0、Y1 、Y2的函数式: Y2 Y1 Y0 ABD CD BD CD 例 试分析下列电路的逻辑功能,指出该电路的用途

将上述函数式转换成真值表 Y2 =ABD+CD,YI=ACD+BCD+BCD,Yo=BD+CD 输 人 输 出 D C B A Y2 Y Yo 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 ) 0 0 2 0 0 1 1 0 1 0 1 9 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 0 0 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 0 0
将上述函数式转换成真值表 Y2 =ABD+CD, Y1=ACD+BCD+BCD, Y0=BD+CD

从真值表可看出: 当DCBA表示的二进制数小于或等于5时,Yo=1; 当DCBA表示的二进制数在6和10之间时,Y1=1; 当DCBA表示的二进制数大于或等于11时,Y2=1;
从真值表可看出: 当DCBA表示的二进制数小于或等于5时,Y0=1; 当DCBA表示的二进制数在6和10之间时,Y1=1; 当DCBA表示的二进制数大于或等于11时,Y2=1;

4.2组合逻辑电路的设计方法 逻辑电路的设计: 根据给出的实际逻辑问题,求出实现 这一逻辑功能的最简单逻辑电路。 (实际逻辑问题→电路)
4.2组合逻辑电路的设计方法 逻辑电路的设计: 根据给出的实际逻辑问题,求出实现 这一逻辑功能的最简单逻辑电路。 (实际逻辑问题 电路)

数字逻辑电路的设计过程可分为两个阶段: 由逻辑功能的文字描述→逻辑描述(例 真值表); 逻辑描述之间的转换(例从真值表 逻辑图)
数字逻辑电路的设计过程可分为两个阶段: 由逻辑功能的文字描述→逻辑描述(例 真值表); 逻辑描述之间的转换(例 从真值表→ 逻辑图)