
第三节晶体二极管电路 的分析方法
第三节 晶体二极管电路 ————的分析方法

1.3.1晶体二极管模型 在分析电路时,电路中的各个实际器件,都必须用相应的 模型来表示。力求采用最简单的模型,使电路分析简化,便 于从分析结果中直观地揭示电路的主要特性。 实际器件的模型,可以用各种形式构成: (1)、用数学表达式构成的数学模型; (2)、用曲线和表格形式构成的曲线和表格模型; (3)、用理想电路元件构成的电路模型: (4)、还可以用多种形式构成的混合模型;
1.3.1 晶体二极管模型 在分析电路时,电路中的各个实际器件,都必须用相应的 模型来表示。力求采用最简单的模型,使电路分析简化,便 于从分析结果中直观地揭示电路的主要特性。 实际器件的模型,可以用各种形式构成: (1)、用数学表达式构成的数学模型; (2)、用曲线和表格形式构成的曲线和表格模型; (3)、用理想电路元件构成的电路模型; (4)、还可以用多种形式构成的混合模型;

一、晶体二极管电路的数学模型: 在理想相条件下,推导出的数学表达式: ID =Is(e 此表达示称为晶体二极管的理想指数模型。 如果,为了反映实际器件的伏安特性,通常的做法是 将上式加以修正。 V-Irs I=Is(e nx-1) 或 =irs +nvr In(+
一、晶体二极管电路的数学模型: 在理想相条件下,推导出的数学表达式: = ( −1) VT V I D I S e 此表达示称为晶体二极管的理想指数模型。 如果,为了反映实际器件的伏安特性,通常的做法是 将上式加以修正。 = ( −1) − T S n V V Ir I I S e 或 ln(1 ) S S T I I V = Ir + nV +

V-Irs I=Is(e nv, -1) 式中n称为非理想化因子,其值与I有关。 当I为正常值时,n≈1。 当过小或过大,n≈2。 [s是与PN结相串联的电阻。(中性区的体电阻、接触 电阻、金属引线电阻) 如果,进一步考虑击穿特性和非线性电容特性,那么, 模型将会变得更为复杂
= ( −1) − T S n V V Ir I I S e 式中 n 称为非理想化因子,其值与I有关。 当I为正常值时,n ≈ 1 。 当I过小或过大, n ≈ 2 。 r S 是与PN结相串联的电阻。(中性区的体电阻、接触 电阻、金属引线电阻) 如果,进一步考虑击穿特性和非线性电容特性,那么, 模型将会变得更为复杂
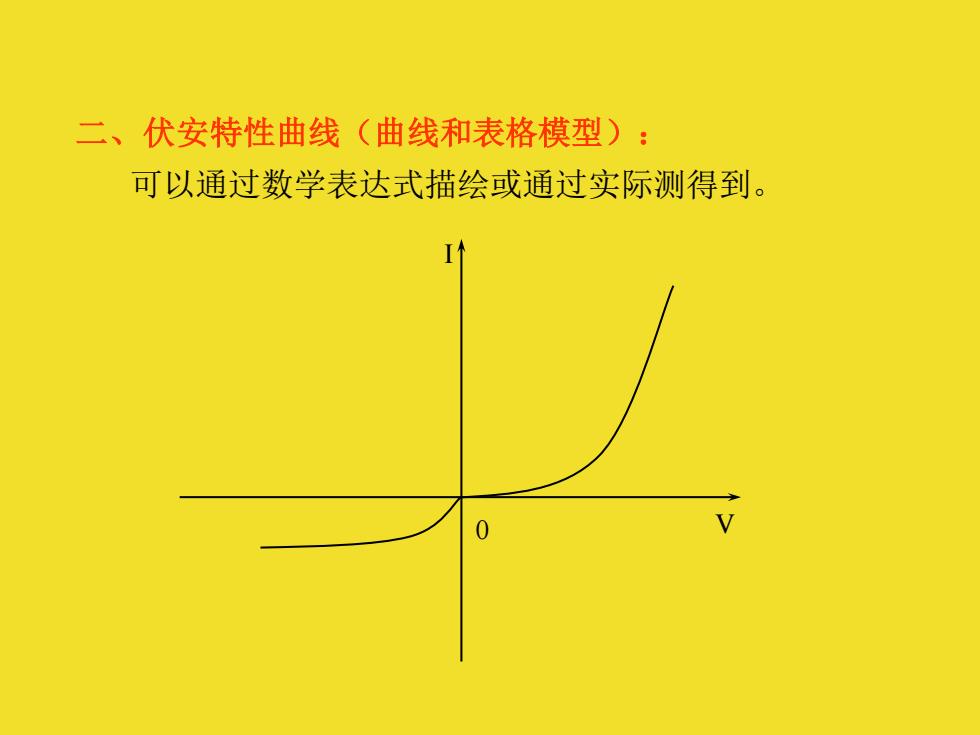
二、伏安特性曲线(曲线和表格模型): 可以通过数学表达式描绘或通过实际测得到
二、伏安特性曲线(曲线和表格模型): 可以通过数学表达式描绘或通过实际测得到。 0 I V
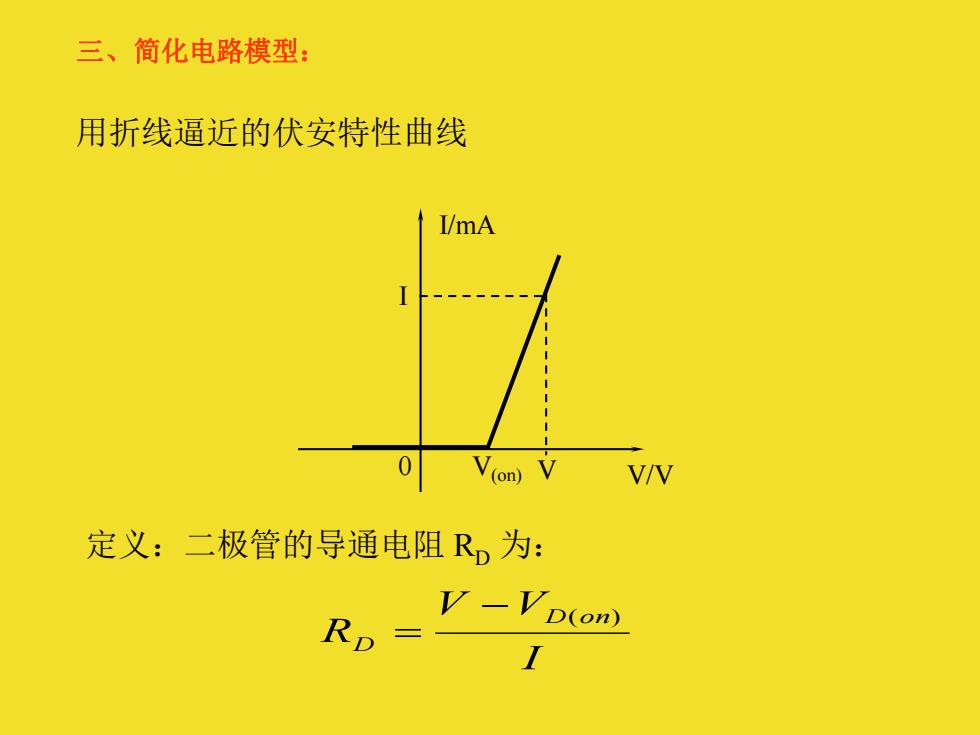
三、简化电路模型: 用折线逼近的伏安特性曲线 I/mA V(on)V V/V 定义:二极管的导通电阻R,为: RD= V-Vp(on)
用折线逼近的伏安特性曲线 V I 0 V(on) I/mA V/V 定义:二极管的导通电阻 RD 为: I V V R D on D − ( ) = 三、简化电路模型:
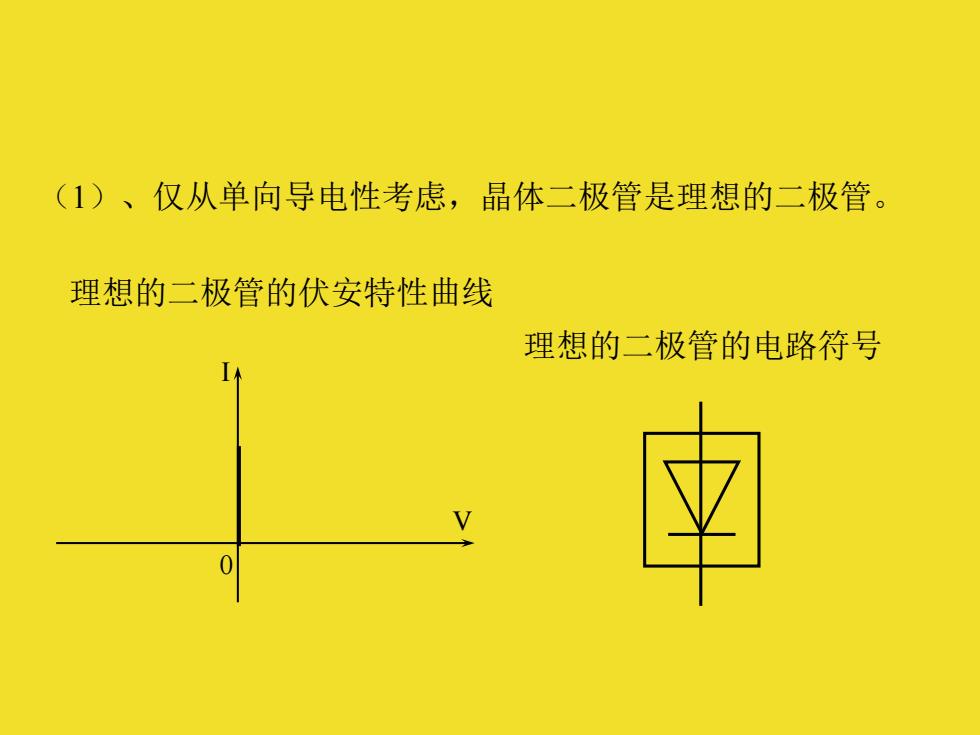
(1)、仅从单向导电性考虑,晶体二极管是理想的二极管。 理想的二极管的伏安特性曲线 理想的二极管的电路符号
(1)、仅从单向导电性考虑,晶体二极管是理想的二极管。 理想的二极管的伏安特性曲线 0 I V 理想的二极管的电路符号
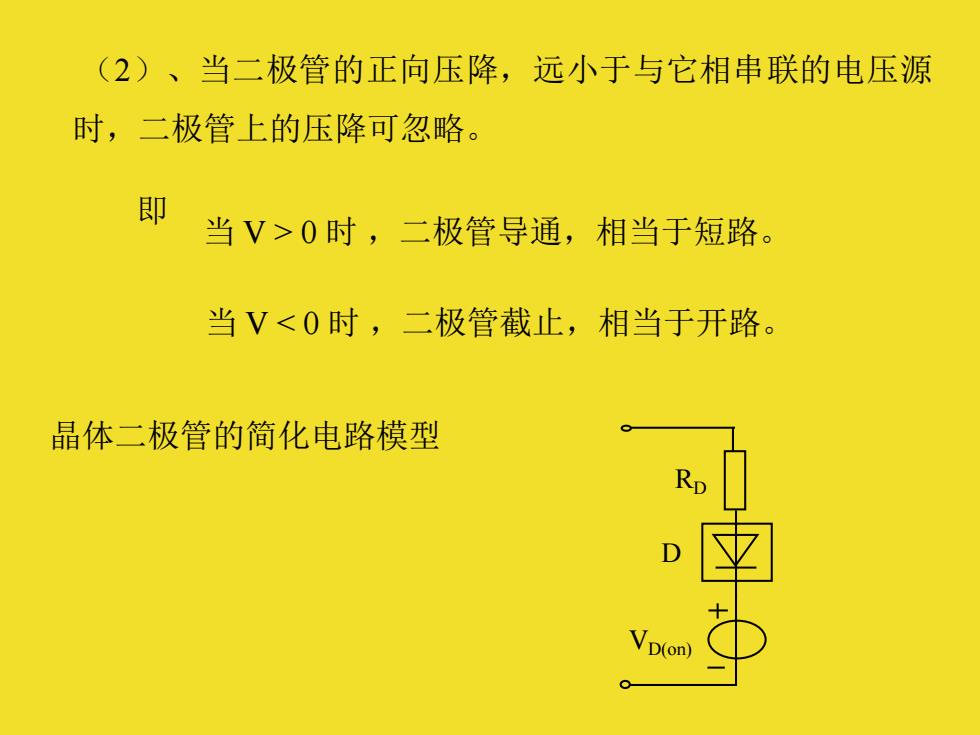
(2)、当二极管的正向压降,远小于与它相串联的电压源 时,二极管上的压降可忽略。 即 当V>0时,二极管导通,相当于短路。 当V<0时,二极管截止,相当于开路。 晶体二极管的简化电路模型 RD D √D(on
(2)、当二极管的正向压降,远小于与它相串联的电压源 时,二极管上的压降可忽略。 即 当 V > 0 时 ,二极管导通,相当于短路。 当 V < 0 时 ,二极管截止,相当于开路。 晶体二极管的简化电路模型 RD D VD(on)

四、小信号电路模型: 如果,加到二极管上的电压是由直流电压V。和叠加 在其上的增量电压△V组成。 即V=V。+AV则,相应产生的电流为,I=I。+△I I/mA △V 1 111 V/V 图中,V。与o在伏安特性曲线上对应的点,称为静态 工作点,用Q表示
四、小信号电路模型: 如果,加到二极管上的电压是由直流电压VQ 和叠加 在其上的增量电压ΔV 组成。 即 V = VQ +ΔV 则,相应产生的电流为,I = IQ +ΔI Q ΔI ΔV 0 IQ I/mA V/V VQ 图中,VQ 与 IQ 在伏安特性曲线上对应的点,称为静态 工作点,用 Q表示
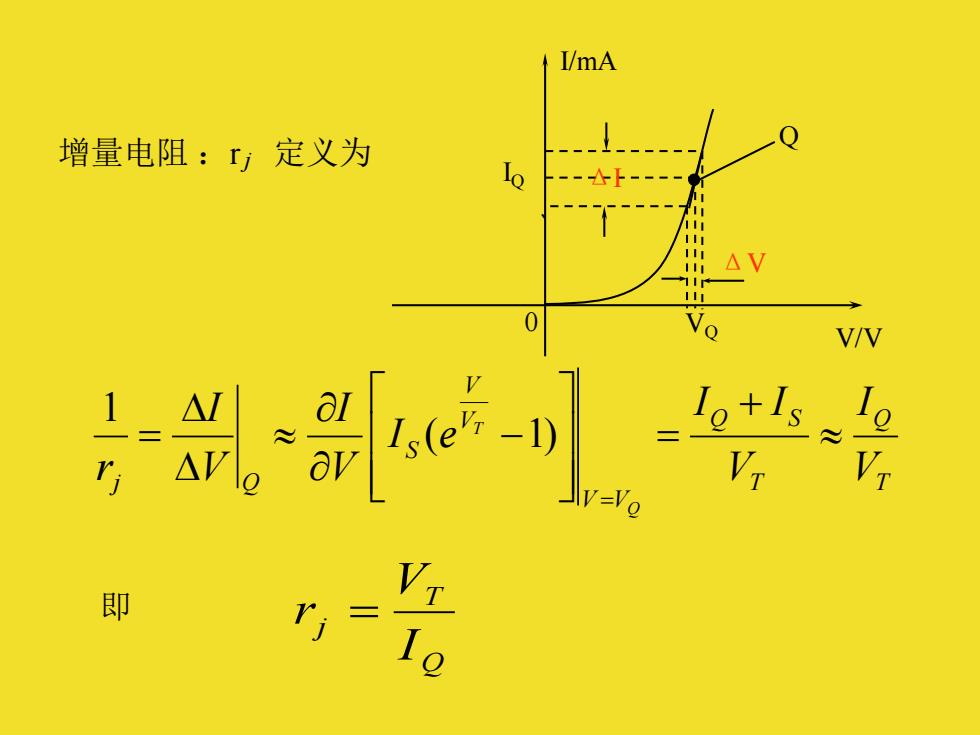
I/mA 增量电阻:r定义为 △V Vo V/V -1g+1s V V-V. 即 V Ie
增量电阻 :r 定义为 T Q T Q S V V V V S j Q V I V I I I e V I V I r Q T + = − = = ( 1) 1 即 Q T j I V r = Q ΔI ΔV 0 IQ I/mA V/V VQ j