
第五节晶体三极管 的小信号电路模型
第五节 晶体三极管 ————的小信号电路模型
当叠加在Q点上的各交流量足够小时,它们之间的关 系可近似用线性函数描述,则相应等效的线性电路,就是 晶体三极管的小信号电路模型。 假如,在晶体三极管各极直流电压和电流上叠加一增量电压 和电流(即交流量)。 如图所示:以共发射极组态为例 根据电路有 iB=lBO+元,'BE=VBEQ+Vbe VBB ic=Ico+ic YCE=VCEQ Yce 其中,Bo,co,VBo,Vco为直流分量,是由直 流静态工作点Q点所确定的电压和电流
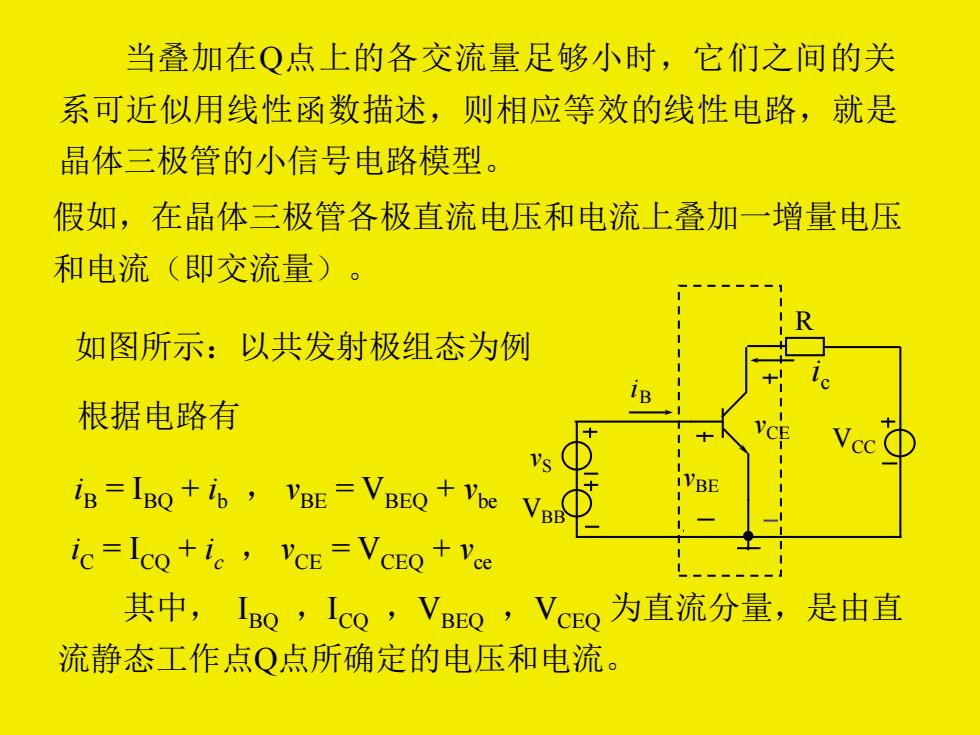
当叠加在Q点上的各交流量足够小时,它们之间的关 系可近似用线性函数描述,则相应等效的线性电路,就是 晶体三极管的小信号电路模型。 假如,在晶体三极管各极直流电压和电流上叠加一增量电压 和电流(即交流量)。 如图所示:以共发射极组态为例 vS iB vBE R vCE VCC VBB i c 根据电路有 iB = IBQ + i b , vBE = VBEQ + vbe iC = ICQ + i c , vCE = VCEQ + vce 其中, IBQ ,ICQ ,VBEQ ,VCEQ 为直流分量,是由直 流静态工作点Q点所确定的电压和电流

注意:为了避免符号混淆,应服从下面约定。 (1)、大写字母、大写下标,表示直流量。 例如、VE等等,如增加下标Q,是用来限定Q点上 的直流量,如O、VEO等。 (2)、小写字母、小写下标,表示交流量。 例如、Ve等。 (3)、小写字母、大写下标,表示总瞬时量。 例如、iB、YE等
注意:为了避免符号混淆,应服从下面约定。 (1)、大写字母、大写下标,表示直流量。 例如、 IB 、VBE 等等,如增加下标Q ,是用来限定Q 点上 的直流量,如 IBQ 、VBEQ 等。 (2)、小写字母、小写下标,表示交流量。 例如、 i b 、vbe 等。 (3)、小写字母、大写下标,表示总瞬时量。 例如、iB 、vBE 等
晶体三极管可等效为如图所示的二端网络 VBE 双口网络 VCE 晶体三极管的小信号电路模型,可以通过数学分析 逐步推导出: 对四个变量B、e、yE、VcE可以用其中的两个变 量作为自变量,另外两个变量作为自变量的非线性函数。 例如、取i与vCE作为自变量。 则有输入回路的非线性函数 VBE f(ig'VCE) 输出回路的非线性函数 e=f2(iB,vE》
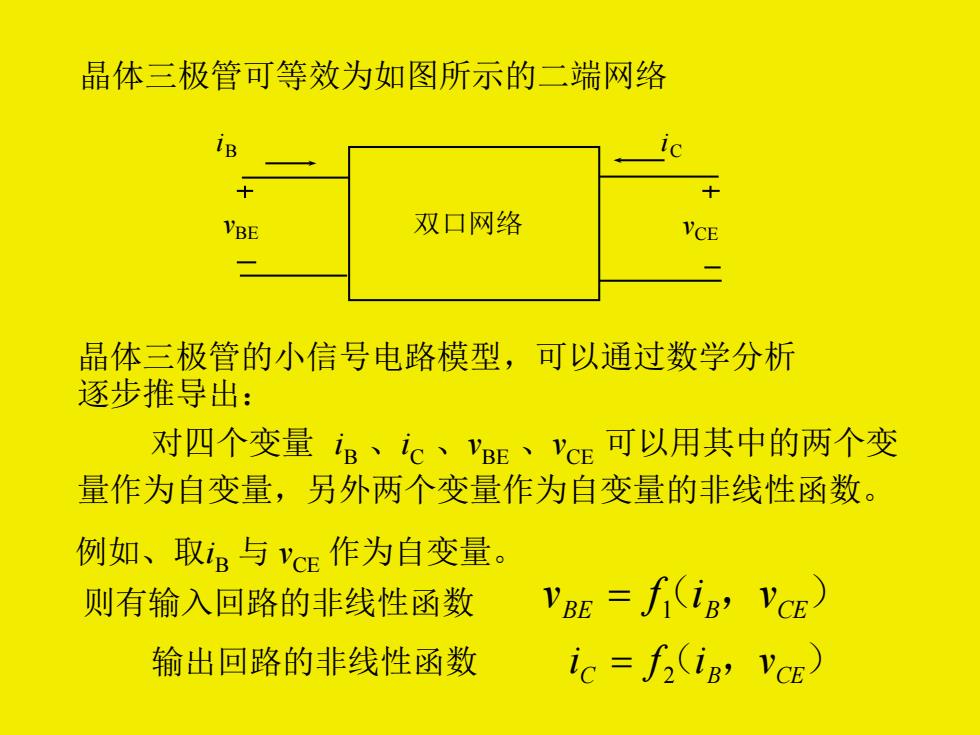
晶体三极管可等效为如图所示的二端网络 iB vBE vCE iC 双口网络 晶体三极管的小信号电路模型,可以通过数学分析 逐步推导出: 对四个变量 iB 、iC 、vBE 、vCE 可以用其中的两个变 量作为自变量,另外两个变量作为自变量的非线性函数。 例如、取iB 与 vCE 作为自变量。 则有输入回路的非线性函数 vBE = f(1 i B ,vCE) 输出回路的非线性函数 i C = f(2 i B ,vCE)

用幂级数在Q点上对交流量展开,得 VBE f(IBo'VcEe)+ ∂NBE OV BE Ve+.+高阶项 OV CEo ie=f1gVao+aing Dic Dic Ve+.+高阶项 其中 VBEQ f(I ng'VCEQ)YBE -VBE Yhe Ice =f2(IBe'VcEe)>ic-Ice =ic 所以
用幂级数在Q点上对交流量展开,得 + + + = + ce CE Q B E b B Q B E B E B Q CEQ v v v i i v v f(1 I ,V ) 高阶项 + + + = + ce CE Q C b B Q C C B Q CEQ v v i i i i i f(2 I ,V ) 高阶项 其中 VBEQ = f(1 I BQ,VCEQ) BE BEQ be v −V = v I CQ = f(2 I BQ,VCEQ) C CQ c i − I = i 所以
若交流量很小,则高阶项可以忽略。 OV BE Vbe OV BE OiB lo OV CE\o ∂ic OiB\o
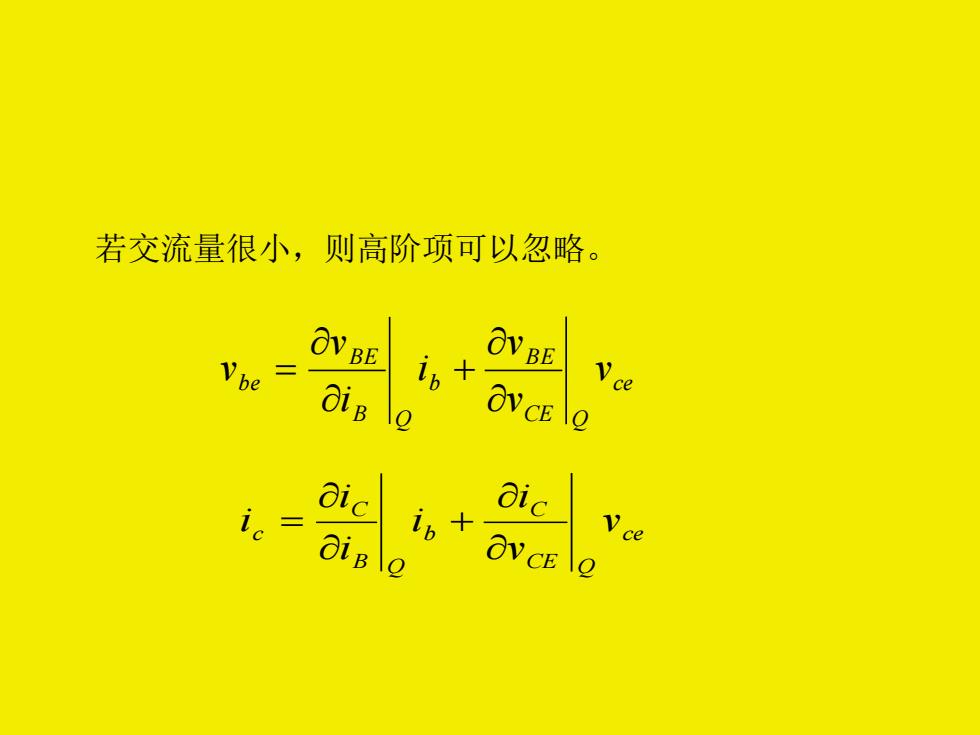
若交流量很小,则高阶项可以忽略。 ce CE Q B E b B Q B E b e v v v i i v v + = ce CE Q C b B Q C c v v i i i i i + =

若取、VgE、CE为自变量 则有输入回路的非线性函数 iB f(VBE'VCE) 则有输出回路的非线性函数 ic =f(VBE'VCE> 用幂级数在Q点上对交流量展开,得: 。=fV Veu+aglo iB Ve十.+高阶项 a+o0c leV Ve十.+高阶项
若取 、vBE 、vCE 为自变量 则有输入回路的非线性函数 i B = f(1 vBE,vCE) 则有输出回路的非线性函数 i C = f(2 vBE,vCE) 用幂级数在Q点上对交流量展开,得: + + + = + ce CE Q B b e B E Q B B BEQ CEQ v v i v v i i f(1 V ,V ) 高阶项 + + + = + ce CE Q C b e B E Q C C BEQ CEQ v v i v v i i f(2 V ,V ) 高阶项
其中10=f(VBEO VCE0)→igB-IBo=b Ico=f2(IRO VCEQ)→ic-Ico=i。 所以 ip= OiB Vbe 十 Ve+.+高阶项 OV BE\O OVCE \O i= Dic Ve+.+高阶项 OV BE\O OVCE o
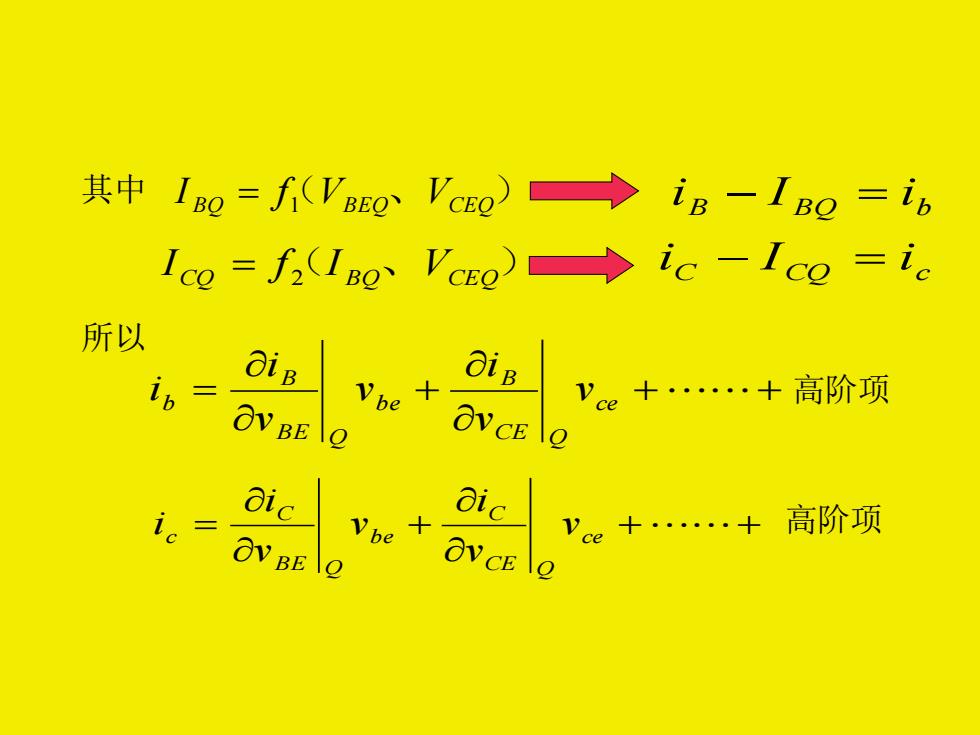
其中 I BQ = f ( 1 VBEQ 、 VCEQ ) B BQ b i − I = i I CQ = f ( 2 I BQ 、 VCEQ ) C CQ c i − I = i 所以 + + + = ce CE Q B b e B E Q B b v vi v vi i 高阶项 + + + = ce CE Q C b e B E Q C c v vi v vi i 高阶项

若交流量很小,则高阶项可以忽略。 因此,可得:i6= OiB OiB Vbe+ ce OV BE\O OVCE\ dic Vbe 十 oic OV BE OVCEle 令、 OiB OiB OV BE\Q gbe = Dic 8m= OV BE gce Ov CE o
若交流量很小,则高阶项可以忽略。 因此,可得: ce CE Q B b e B E Q B b v v i v v i i + = ce CE Q C b e B E Q C c v v i v v i i + = 令 、 BE Q B be v i g = CE Q B bc v i g = BE Q C m v i g = CE Q C ce v i g =
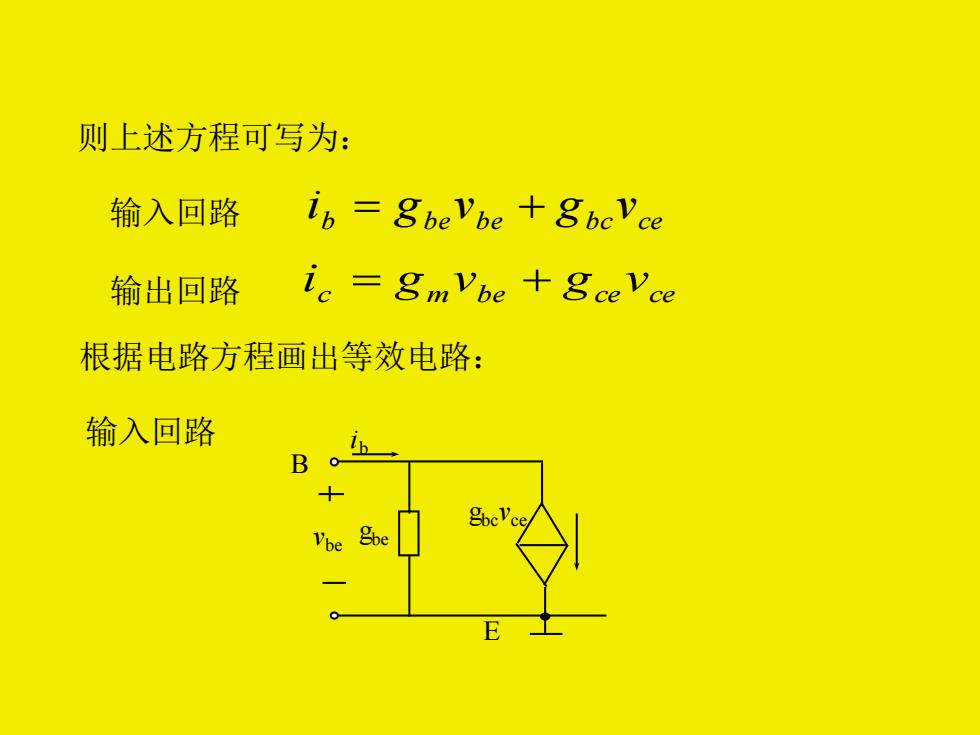
则上述方程可写为: 输入回路 Ib =gbeVbe +gbcVce 输出回路 ic =gmvbe +gceVce 根据电路方程画出等效电路: 输入回路 ● he
则上述方程可写为: 输入回路 b be be bc ce i = g v + g v 输出回路 c gm vbe gce vce i = + 根据电路方程画出等效电路: 输入回路 ib gbcvce vbe B E gbe