钢管订购和运输优化模型 要铺设一条A→42→.→A5的输送天然气的主管道,如图1所示(见反 面).经筛选后可以生产这种主管道钢管的钢厂有S,S2,.,S,·图中粗线表示铁 路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或 者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示 里程(单位:km). 为方便计,1km主管道钢管称为1单位钢管. 一个钢厂如果承担制造这种钢管,至少需要生产500个单位.钢厂S,在指定期 限内能生产该钢管的最大数量为3,个单位,钢管出厂销价1单位钢管为P,万元, 如下表: i 1 2 3 4 5 6 3,80080010002000 20002000 3000 p,160155155160155150 160 1单位钢管的铁路运价如下表: 里程(km)≤300301~350351~400401~450 451-500 运价(万元) 20 23 26 29 32 里程(km) 501~600601-700 701~800801~900901~1000 运价(万元) 37 44 50 55 60 1000km以上每增加1至100km运价增加5万元, 公路运输费用为1单位钢管每千米0.1万元(不足整千米部分按整千米计算). 钢管可由铁路、公路运往铺设地点(不只是运到点A,42,.,45,而是管道 全线)
1 钢管订购和运输优化模型 要铺设一条 A1 → A2 →→ A15 的输送天然气的主管道, 如图 1 所示(见反 面).经筛选后可以生产这种主管道钢管的钢厂有 1 2 7 S S S , , , .图中粗线表示铁 路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或 者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示 里程(单位:km). 为方便计,1km 主管道钢管称为 1 单位钢管. 一个钢厂如果承担制造这种钢管,至少需要生产 500 个单位.钢厂 i S 在指定期 限内能生产该钢管的最大数量为 i s 个单位,钢管出厂销价 1 单位钢管为 i p 万元, 如下表: i 1 2 3 4 5 6 7 i s 800 800 1000 2000 2000 2000 3000 i p 160 155 155 160 155 150 160 1 单位钢管的铁路运价如下表: 里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 20 23 26 29 32 里程(km) 501~600 601~700 701~800 801~900 901~1000 运价(万元) 37 44 50 55 60 1000km 以上每增加 1 至 100km 运价增加 5 万元. 公路运输费用为 1 单位钢管每千米 0.1 万元(不足整千米部分按整千米计算). 钢管可由铁路、公路运往铺设地点(不只是运到点 1 2 15 A , A , , A ,而是管道 全线)
问题: (1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用) 思考题: (2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用 影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并 给出相应的数字结果 (3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构 成网络,请就这种更一般的情形给出一种解决办法,并对图2按(1)的要求给出 模型和结果. 9 30 1200 17 110 500 1100 210 480 195 3001 115 20 10 45 94 6064 图1 104 2
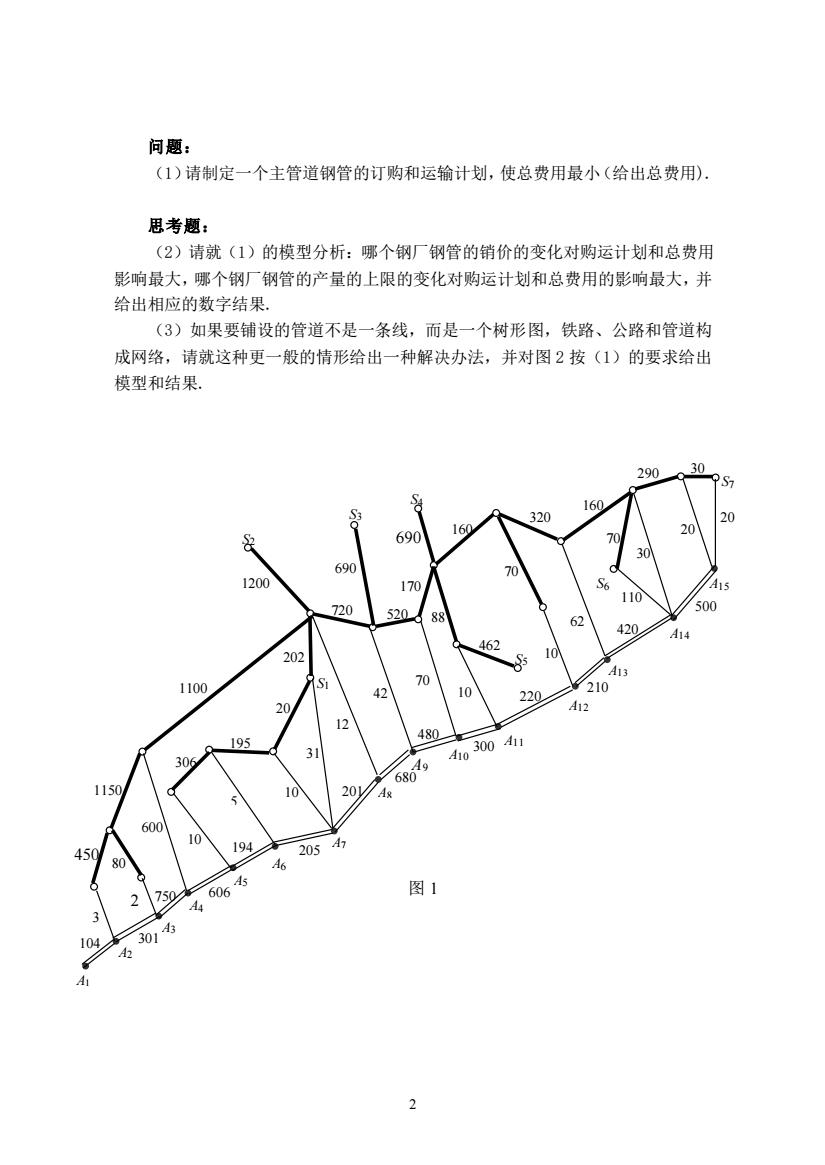
2 问题: (1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用). 思考题: (2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用 影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并 给出相应的数字结果. (3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构 成网络,请就这种更一般的情形给出一种解决办法,并对图 2 按(1)的要求给出 模型和结果. A1 3 2 5 80 10 10 31 20 12 42 70 10 88 10 70 62 70 30 20 20 30 450 104 301 750 606 194 205 201 680 480 300 220 210 420 500 600 306 0 195 202 720 690 520 170 690 462 160 320 160 110 290 1150 1100 1200 A2 A3 A4 A5 A6 A7 A1 1 A8 A1 1 A9 11 A1 1 A10 A11 A12 A13 A14 A15 S1 S2 S3 S4 S5 S6 S7 图 1
29 20 1100 210 220 A13 199 0 4o300 1150 600 450 205 759% 4605 图2 一、基本假设 1.沿铺设的主管道以有公路或者有施工公路 2.在主管道上,每千米卸1单位的钢管 3.公路运输费用为1单位钢管每千米0.1万元(不足整千米部分按整千米计算 4.在计算总费用时,只考虑运输费和购买钢管的费用,而不考虑其他费用 5.在计算钢厂的产量对购运计划影响时,只考虑钢厂的产量足够满足需要的情况, 即钢厂的产量不受限制】 6.假设钢管在铁路运输路程超过1000km时,铁路每增加1至100km,1单位钢管 3
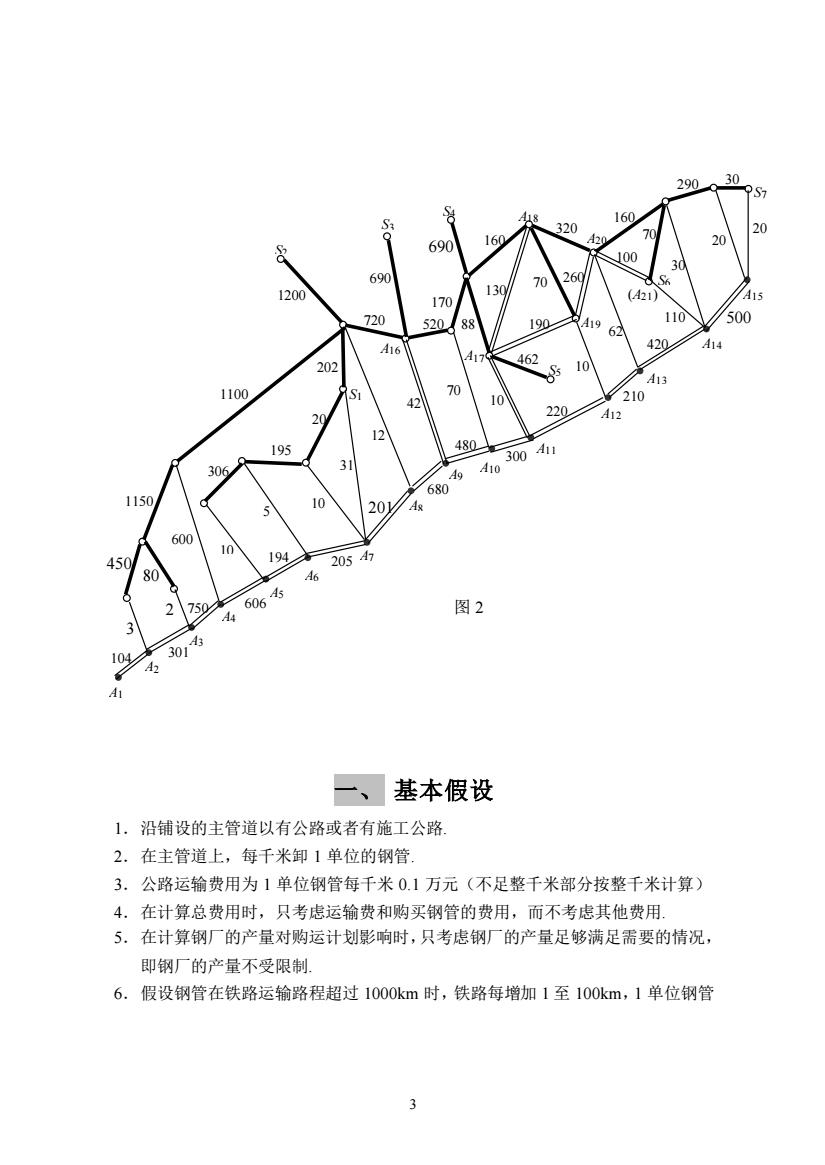
3 一、 基本假设 1.沿铺设的主管道以有公路或者有施工公路. 2.在主管道上,每千米卸 1 单位的钢管. 3.公路运输费用为 1 单位钢管每千米 0.1 万元(不足整千米部分按整千米计算) 4.在计算总费用时,只考虑运输费和购买钢管的费用,而不考虑其他费用. 5.在计算钢厂的产量对购运计划影响时,只考虑钢厂的产量足够满足需要的情况, 即钢厂的产量不受限制. 6.假设钢管在铁路运输路程超过 1000km 时,铁路每增加 1 至 100km,1 单位钢管 A1 3 2 5 80 10 10 31 20 12 42 70 10 88 10 70 62 70 30 20 20 30 450 104 301 750 606 194 205 201 680 480 300 220 210 420 500 600 306 0 195 202 720 690 520 170 690 462 160 320 160 110 290 1150 1100 1200 A19 130 190 260 100 A2 A3 A4 A5 A6 A7 A8 A1 1 A9 A10 A11 A12 A13 A14 A15 S1 S2 S3 S4 S5 S6 S7 A16 A17 A18 A20 (A21) 图 2

的运价增加5万元, 二、符号说明: S,:第i个钢厂: i=1,2,.,7 S,:第i个钢厂的最大产量: i=1,2,.,7 A:输送管道(主管道)上的第j个点: j=1,2,.,15 P,:第i个钢厂1单位钢管的销价 i=1,2,.,7 x:钢厂S,向点A,运输的钢管量: i=12,.,7j=1,2,.15 1,:在点A,与点A之间的公路上,运输点A,向点A方向铺设的钢管量: j=1,2,3,.,14(41=0) a):1单位钢管从钢厂S运到结点A,的最少总费用,即公路运费、铁路运费和 钢管销价之和: i=1,2.,7 j=1,2,.,15 b,:与点A,相连的公路和铁路的相交点: j=2,3.,15 A41:相邻点A,与A1之间的距离: j-1,2,.,14 三、模型的建立与求解 问题一:讨论如何调整主管道钢管的订购和运输方案使总费用最小 由题意可知,钢管从钢厂S,到运输结点A,的费用a,包括钢管的销价、钢管的 铁路运输费用和钢管的公路运输费用在费用,最小时,对钢管的订购和运输进行 分配,可得出本问题的最佳方案 1.求钢管从钢厂S,运到运输点A,的最小费用 1)将图1转换为一系列以单位钢管的运输费用为权的赋权图
4 的运价增加 5 万元. 二、符号说明: i S :第 i 个钢厂; i = 1,2, ,7 i s :第 i 个钢厂的最大产量; i = 1,2, ,7 Aj :输送管道(主管道)上的第 j 个点; j = 1,2, ,15 i p :第 i 个钢厂 1 单位钢管的销价; i = 1,2, ,7 ij x :钢厂 i S 向点 Aj 运输的钢管量; i = 1,2, ,7 j = 1,2, ,15 j t :在点 Aj 与点 Aj+1 之间的公路上,运输点 Aj 向点 Aj+1 方向铺设的钢管量; j = 1,2,3, ,14 ( t 1 = 0 ) ij a :1 单位钢管从钢厂 Si 运到结点 Aj 的最少总费用,即公路运费﹑铁路运费和 钢管销价之和; i = 1,2, ,7 j = 1,2, ,15 bj :与点 Aj 相连的公路和铁路的相交点; j = 2,3, ,15 Aj. j+1 :相邻点 Aj 与 Aj+1 之间的距离; j = 1,2, ,14 三、模型的建立与求解 问题一:讨论如何调整主管道钢管的订购和运输方案使总费用最小 由题意可知,钢管从钢厂 i S 到运输结点 Aj 的费用 ij a 包括钢管的销价﹑钢管的 铁路运输费用和钢管的公路运输费用.在费用 ij a 最小时,对钢管的订购和运输进行 分配,可得出本问题的最佳方案. 1. 求钢管从钢厂 i S 运到运输点 Aj 的最小费用 1)将图 1 转换为一系列以单位钢管的运输费用为权的赋权图

由于钢管从钢厂S,运到运输点A,要通过铁路和公路运输,而铁路运输费用是 分段函数,与全程运输总距离有关又由于钢厂S直接与铁路相连,所以可先求出 钢厂S到铁路与公路相交点b,的最短路径如图3 图3铁路网络图 依据钢管的铁路运价表,算出钢厂S到铁路与公路相交点b,的最小铁路运输 费用,并把费用作为边权赋给从钢厂S,到b,的边再将与b,相连的公路、运输点A 及其与之相连的要铺设管道的线路(也是公路)添加到图上,根据单位钢管在公路 上的运价规定,得出每一段公路的运费,并把此费用作为边权赋给相应的边.以S为 例得图4
5 由于钢管从钢厂 i S 运到运输点 Aj 要通过铁路和公路运输,而铁路运输费用是 分段函数,与全程运输总距离有关.又由于钢厂 i S 直接与铁路相连,所以可先求出 钢厂 i S 到铁路与公路相交点 j b 的最短路径.如图 3 图 3 铁路网络图 依据钢管的铁路运价表,算出钢厂 i S 到铁路与公路相交点 j b 的最小铁路运输 费用,并把费用作为边权赋给从钢厂 i S 到 j b 的边.再将与 j b 相连的公路、运输点 Ai 及其与之相连的要铺设管道的线路(也是公路)添加到图上,根据单位钢管在公路 上的运价规定,得出每一段公路的运费,并把此费用作为边权赋给相应的边.以 1 S 为 例得图 4
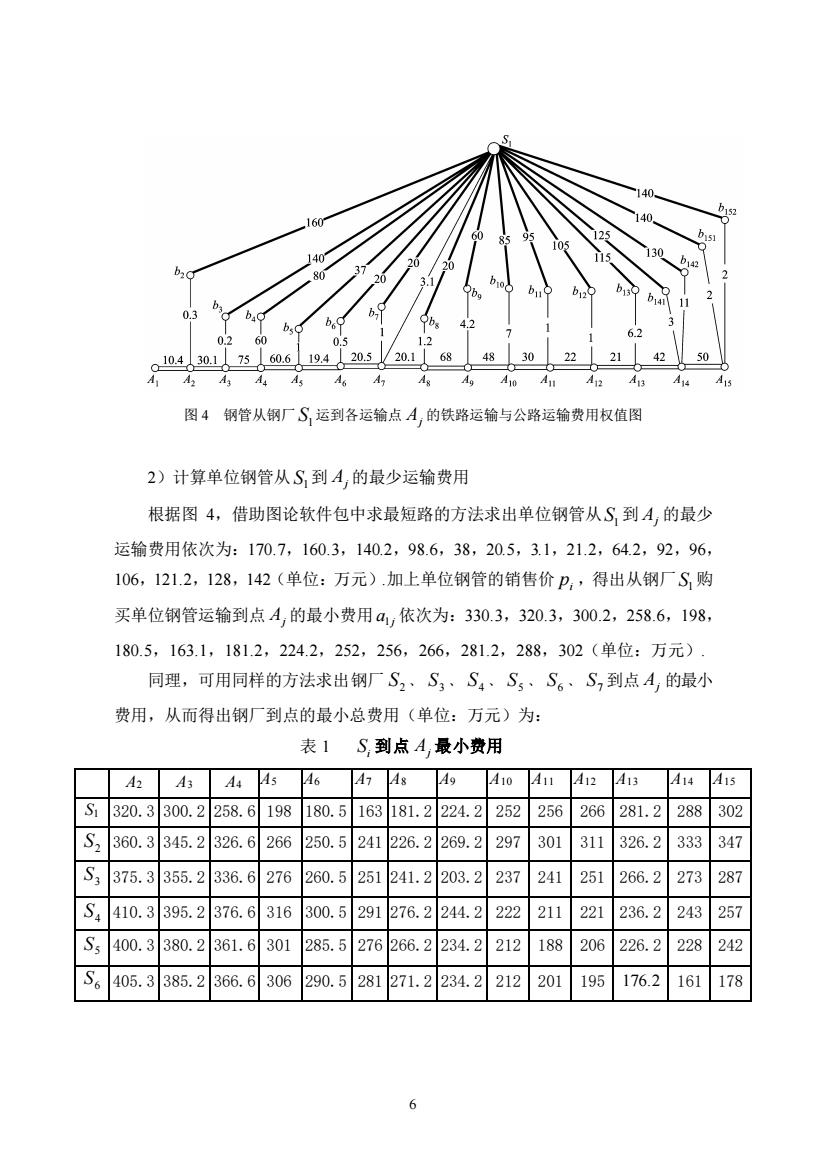
. 02 10430.1560619.420.520.1L684830222142 50 A A A 图4钢管从钢厂S运到各运输点A,的铁路运输与公路运输费用权值图 2)计算单位钢管从S,到A,的最少运输费用 根据图4,借助图论软件包中求最短路的方法求出单位钢管从S,到A,的最少 运输费用依次为:170.7,160.3,140.2,98.6,38,20.5,3.1,21.2,64.2,92,96 106,121.2,128,142(单位:万元).加上单位钢管的销售价p,得出从钢厂S购 买单位钢管运输到点A,的最小费用a,依次为:330.3,320.3,300.2,258.6,198, 180.5,163.1,181.2,224.2,252,256,266,281.2,288,302(单位:万元). 同理,可用同样的方法求出钢厂S2、S、S4、S、S6、S,到点4,的最小 费用,从而得出钢厂到点的最小总费用(单位:万元)为: 表1S到点A,最小费用 A2 AA44546 g 410A111241314415 S320.3300.2258.6198180.5163181.2224.2252256266281.2288302 S2360.3345.2326.6266 50.5241226.2269.2297 301311326.2333347 S3375.3355.2 36.6276260.52512 41.2203.2 237241251 266.2273 287 S4410.3395.2376.6316300.5291276.2244.2222211 221236.2243 257 S,400.3380.2361.6301285.5276 266.2234.2212 188206 226.2 242 S6405.3385.2366.6306290.5281271.2234. 2212201195176.2161178
6 图 4 钢管从钢厂 1 S 运到各运输点 Aj 的铁路运输与公路运输费用权值图 2)计算单位钢管从 1 S 到 Aj 的最少运输费用 根据图 4,借助图论软件包中求最短路的方法求出单位钢管从 1 S 到 Aj 的最少 运输费用依次为:170.7,160.3,140.2,98.6,38,20.5,3.1,21.2,64.2,92,96, 106,121.2,128,142(单位:万元).加上单位钢管的销售价 i p ,得出从钢厂 1 S 购 买单位钢管运输到点 Aj 的最小费用 j a1 依次为:330.3,320.3,300.2,258.6,198, 180.5,163.1,181.2,224.2,252,256,266,281.2,288,302(单位:万元). 同理,可用同样的方法求出钢厂 2 S ﹑ 3 S ﹑ 4 S ﹑ 5 S ﹑ 6 S ﹑ 7 S 到点 Aj 的最小 费用,从而得出钢厂到点的最小总费用(单位:万元)为: 表 1 i S 到点 Aj 最小费用 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 S1 320.3 300.2 258.6 198 180.5 163 181.2 224.2 252 256 266 281.2 288 302 2 S 360.3 345.2 326.6 266 250.5 241 226.2 269.2 297 301 311 326.2 333 347 3 S 375.3 355.2 336.6 276 260.5 251 241.2 203.2 237 241 251 266.2 273 287 4 S 410.3 395.2 376.6 316 300.5 291 276.2 244.2 222 211 221 236.2 243 257 5 S 400.3 380.2 361.6 301 285.5 276 266.2 234.2 212 188 206 226.2 228 242 6 S 405.3 385.2 366.6 306 290.5 281 271.2 234.2 212 201 195 176.2 161 178

S,425.3405.2386.6326310.5301291.2259.223726216198.2186162 2.建立模型 运输总费用可分为两部分: 运输总费用-钢厂到各点的运输费用+铺设费用. 运输费用:若运输点A,向钢厂S订购x,单位钢管,则钢管从钢厂S,运到运 输点A,所需的费用为a1由于钢管运到A,必须经过A,所以可不考虑A,那 157 么所有钢管从各钢厂运到各运输点上的总费用为:之4 铺设费用:当钢管从钢厂S运到点A,后,钢管就要向运输点A,的两边A,A 段和A,-1A,段运输(铺设)管道设A,向A,A段铺设的管道长度为y,则A,向 44蜘段的运输费用为01x0+2++y)北,+l(万元:由于相都运输点 20 A,与A4之间的距离为A4,那么AH向A,A段铺设的管道长为A1-1, 所对应的铺设费用为色-+-》(万元)所以,主管道上的铺设费 20 用为:先,色n-+北小 20 20 总费用为:1-224,+芝型,色m-+北6-小 715 20 20 又因为一个钢厂如果承担制造钢管任务,至少需要生产500个单位,钢厂S,在 指定期限内最大生产量为5,个单位,放50≤,≤或或之,=0因此本 问题可建立如下的非线性规划模型: mimf-2,+D,4-X+1-2+22a 20 20 2,=%j=2315 15 st500s∑,≤或2x,=0 y201=1,.,7j=2.,15 0≤1,≤AmH 7
7 7 S 425.3 405.2 386.6 326 310.5 301 291.2 259.2 237 226 216 198.2 186 162 2. 建立模型 运输总费用可分为两部分: 运输总费用=钢厂到各点的运输费用+铺设费用. 运输费用:若运输点 Aj 向钢厂 i S 订购 ij x 单位钢管,则钢管从钢厂 i S 运到运 输点 Aj 所需的费用为 ij ij a x .由于钢管运到 A1 必须经过 A2 ,所以可不考虑 A1 ,那 么所有钢管从各钢厂运到各运输点上的总费用为: = = 15 2 7 j i 1 ijaij x . 铺设费用:当钢管从钢厂 i S 运到点 Aj 后,钢管就要向运输点 Aj 的两边 Aj Aj+1 段和 Aj−1Aj 段运输(铺设)管道.设 Aj 向 Aj Aj+1 段铺设的管道长度为 j y ,则 Aj 向 Aj Aj+1 段的运输费用为 ( ) 20 1 0.1 (1 2 ) + + + + = j j j t t y (万元);由于相邻运输点 Aj 与 Aj+1 之间的距离为 Aj. j+1 ,那么 Aj+1 向 Aj Aj+1 段铺设的管道长为 j j j A − t . +1 , 所对应的铺设费用为 ( )( ) 20 j. j 1 j 1 j. j 1 j A − t + A − t + + (万元).所以,主管道上的铺设费 用为: ( ) ( )( ) = + + − + − + 14 + 1 . 1 . 1 20 1 20 1 j j j j j j j j j t t A t A t 总费用为: ( ) ( )( ) = = = + + − + − + + = + 7 1 15 2 14 1 . 1 . 1 20 1 20 1 i j j j j j j j j j j i j i j t t A t A t f x a 又因为一个钢厂如果承担制造钢管任务,至少需要生产 500 个单位,钢厂 i S 在 指定期限内最大生产量为 i s 个单位,故 i j ij x s = 15 2 500 或 0 15 2 = j= ij x 因此本 问题可建立如下的非线性规划模型: 14 15 7 . 1 . 1 1 2 1 7 1 15 15 2 2 . 1 ( 1) ( )( 1 ) min ( 20 20 j 2,3, ,15 s.t. 500 0 0 1, ,7, 2, ,15 0 j j j j j j j j ij ij j j i ij j i ij i ij j j ij j j j t t A t A t f x a x n x s x x i j t A + + = = = = = = + + − + − = + + = = = = = 或

3.模型求解 由于他不能直装处理约实条作30∈之,5设公=0,我初阿 先将能条作流为后,≤,将到知下限型 nf=号,+)(4-'X4+1-2+之∑xa 20 20 位5=%j25 st x20i=1,.,7,j=2,.,15 0≤L,≤AH 用MATLAB求解,分析结果后发现购运方案中钢厂S,的生产量不足5O0单位, 下面我们采用不让钢厂S,生产和要求钢厂S,的产量不小于500个单位两种方法计 算: 1)不让钢厂S,生产 计算结果:f=1278632(万元)(此时每个钢厂的产量都满足条件). 2)要求钢厂S,的产量不小于500个单位 计算结果:2=1279664(万元)(此时每个钢厂的产量都满足条件) 比较这两种情况,得最优解为,minf=mim(f,5)=厂=1278632(万元) 具体的购运计划如表2: 表2问题一的订购和调运方案 订购量4 As A6A7 4s4 41o 4u 42 43 4n4 4is 800 0 201133200266 0 00 10 0 S800 17911142950 0 3000 00 10 0 0 S310001391118600 0 6640100 00 0 0 0 0000 0 0000 0 0 0 Ss1015 0 358 2420 00 0 415 0 0 十333621 165 0 0 0 0 0
8 3. 模型求解: 由于 MATLAB 不能直接处理约束条件: i j ij x s = 15 2 500 或 0 15 2 = j= ij x ,我们可 先将此条件改为 i j ij x s = 15 2 ,得到如下模型: 用 MATLAB 求解,分析结果后发现购运方案中钢厂 7 S 的生产量不足 500 单位, 下面我们采用不让钢厂 7 S 生产和要求钢厂 7 S 的产量不小于500个单位两种方法计 算: 1)不让钢厂 7 S 生产 计算结果: f 1 = 1278632(万元)(此时每个钢厂的产量都满足条件). 2)要求钢厂 7 S 的产量不小于 500 个单位 计算结果: f 2 = 1279664 (万元) (此时每个钢厂的产量都满足条件). 比较这两种情况,得最优解为, 1 2 1 min f = min( f , f ) = f =1278632(万元) 具体的购运计划如表 2: 表 2 问题一的订购和调运方案 订购量 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 S1 800 0 201 133 200 266 0 0 0 0 0 0 0 0 0 S2 800 179 11 14 295 0 0 300 0 0 0 0 0 0 0 S3 1000 139 11 186 0 0 0 664 0 0 0 0 0 0 0 S4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 S5 1015 0 358 242 0 0 0 0 0 0 415 0 0 0 0 S6 1556 0 0 0 0 0 0 0 0 0 351 86 333 621 165 S7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 14 15 7 . 1 . 1 1 2 1 7 1 15 2 . 1 ( 1) ( )( 1 ) min ( 20 20 j 2,3, ,15 s.t. 0 1, ,7, 2, ,15 0 j j j j j j j j ij ij j j i ij j i ij i j ij j j j t t A t A t f x a x n x s x i j t A + + = = = = = + + − + − = + + = = = =