
数学建模与数学实验 回归分析
数学建模与数学实验 回归分析

实验目的 1.直观了解回归分析基本内容 2.掌握用数学软件求解回归分析问题. 实验内容 1.回归分析的基本理论. 2.用数学软件求解回归分析问题 3.实验作业
实验目的 实验内容 2.掌握用数学软件求解回归分析问题. 1.直观了解回归分析基本内容. 1.回归分析的基本理论. 3.实验作业. 2.用数学软件求解回归分析问题

回归分析 一元线性回归 多元线性回归 数学模型及定义 *模型参数估计 *检验、预测与控制 性回归(曲线回归) 可线性化的一元非线 数学模型及定义 模型参数估计 检验与预观 *多元线性回归中的 逐步回归分析
一元线性回归 多元线性回归 回归分析 数 学 模 型 及 定 义 * 模 型 参 数 估 计 * 检 验 、 预 测 与 控 制 可 线 性 化 的 一 元 非 线 性 回 归 ( 曲 线 回 归 ) 数 学 模 型 及 定 义 * 模 型 参 数 估 计 逐 步 回 归 分 析 * 多 元 线 性 回 归 中 的 检 验 与 预 测
数学模型 例1测16名成年女子的身高与腿长所得数据如下: 身高 143 145 146 147 149 150 153 154 155 156 158 159 160 162 164 (cm) 腿长 88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102 (cm) 以身高x为横坐标, 以腿长y为纵坐标将这些数据点(x,y,) 在平面直角坐标系上标出 解答 y=Bo+Bx+8 85 40 150 155 160 165 散点图
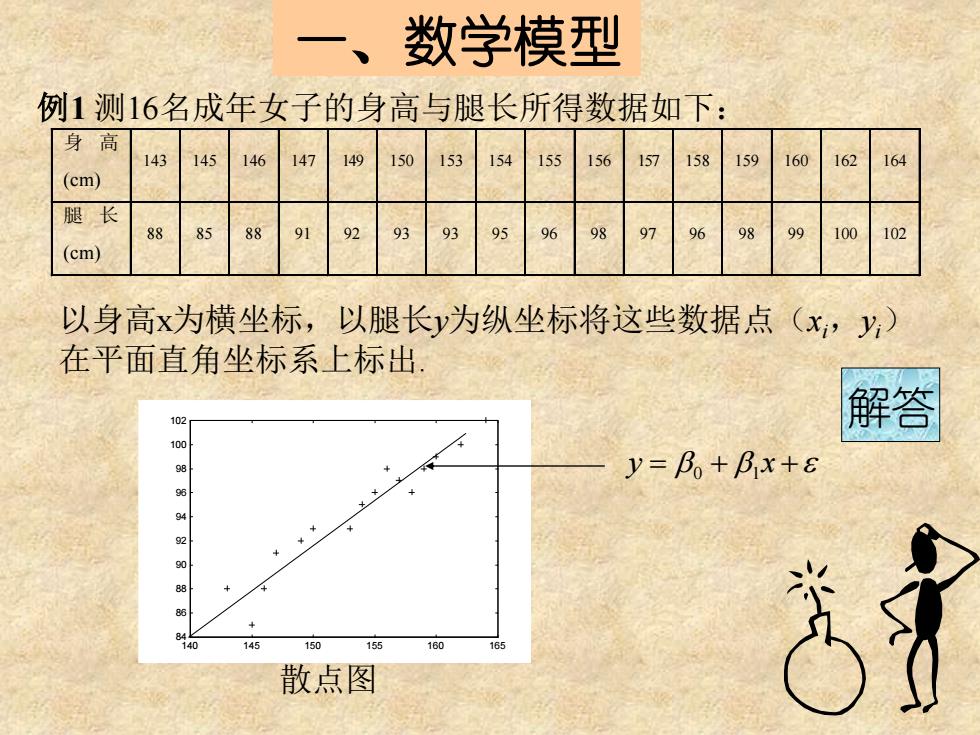
一、数学模型 例1 测16名成年女子的身高与腿长所得数据如下: 身 高 (cm) 143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164 腿 长 (cm) 88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102 以身高x为横坐标,以腿长y为纵坐标将这些数据点(xi,yi) 在平面直角坐标系上标出. 140 145 150 155 160 165 84 86 88 90 92 94 96 98 100 102 散点图 y = + x + 0 1 解答

般地,称由y=B。+Bx+ε确定的模型为一元线性回归模型, 记为 y=B。+Bx+8 E8=0,D8=o2 固定的未知参数B。、B称为回归系数,自变量x也称为回归变量 Y=B。+Bx,称为y对x的回归直线方程 一元线性回归分析的主要任务是: 1.用试验值(样本值)对B。、B和o作点估计: 2.对回归系数B。、阝,作假设检验: 3.在=x。处对y作预测,对y作区间估计 返回
一般地,称由 y = + x + 0 1 确定的模型为一元线性回归模型, 记为 = = = + + 2 0 1 0, E D y x 固定的未知参数 0 、 1 称为回归系数,自变量 x 也称为回归变量. 一元线性回归分析的主要任务是: 1.用试验值(样本值)对 0 、 1 和 作点估计; 2.对回归系数 0 、 1 作假设检验; 3.在 x= 0 x 处对 y 作预测,对 y 作区间估计. Y x = 0 + 1 ,称为 y 对 x 的回归直线方程. 返回

二、模型参数估计 1.回归系数的最小二乘估计 有n组独立观测值(x1,y),(x2,y2),.,(xm,n) y=B。+Bx+6,i=1,2,n 设 E8,=0,D8,-02且6E2,Gn相互独立 记 Q=0B,B)-2=26-R。-Bx月 最小二乘法就是选择B。和B,的估计B。,户,使得 Oa,A)=mmOB,B)
二、模型参数估计 1.回归系数的最小二乘估计 有 n 组独立观测值(x1,y1),(x2,y2),.,(xn,yn) 设 0 1 2 1 2 , 1,2,., 0, ,., i i i i n y x i n E D = + + = = = 且 相互独立 记 ( ) = = = = = − − n i i i n i i Q Q y x 1 2 0 1 1 2 0 1 ( , ) 最小二乘法就是选择 0 和 1 的估计 0 ˆ , 1 ˆ 使得 ) min ( , ) ˆ , ˆ ( 0 1 , 0 1 0 1 Q = Q

B。=-Bx 解得 A-x 女a.6%司 x2-x2 6-功 帅空5空,空四之对 ni= n (经验)回归方程为: =B。+Bx=+B,(x-x)
−− == −2 2 10 1 ˆˆ ˆ x x xy x y y x 解得 (经验)回归方程为: ( ) ˆ ˆ ˆ ˆ 0 1 1 y = + x = y + x − x 或 ( )( ) ( ) = = − − − = ni i ni i i x x x x y y 1 2 1 1 ˆ 其中 = = = = n i i n i i y n x y n x 1 1 1 , 1 , = = = = n i i i n i i x y n x xy n x 1 1 2 2 1 , 1

2.σ2的无偏估计 记Q.=02a)=y-A-月xj=2-)》 称Q。为残差平方和或剩余平方和 σ2的无偏估计为62=Q./(n-2) 称6为剩余方差(残差的方差),62分别与B。、B,独立 G。称为剩余标准差 返回
2. 2 的无偏估计 记 ( ) = = = = − − = − n i n i e i i i i Q Q y x y y 1 1 2 2 0 1 0 1 ( ˆ ) ˆ ˆ ) ˆ , ˆ ( 称 Qe 为残差平方和或剩余平方和. 2 的无偏估计为 ˆ ( 2) 2 e = Qe n − 称 2 ˆ e 为剩余方差(残差的方差), 2 ˆ e 分别与 0 ˆ 、 1 ˆ 独立. e ˆ 称为剩余标准差. 返回

三、检验、预测与控制 1.回归方程的显著性检验 对回归方程Y=阝。+阝x的显著性检验,归结为对假设 H。:B=0,H1:B≠0 进行检验, 假设H。:B1=0被拒绝,则回归显著,认为y与x存在线性关 系,所求的线性回归方程有意义;否则回归不显著,y与x的关系 不能用一元线性回归模型来描述,所得的回归方程也无意义
三、检验、预测与控制 1.回归方程的显著性检验 对回归方程Y x = 0 + 1 的显著性检验,归结为对假设 H0 : 1 = 0;H1 : 1 0 进行检验. 假设 H0 : 1 = 0被拒绝,则回归显著,认为 y 与 x 存在线性关 系,所求的线性回归方程有意义;否则回归不显著,y 与 x 的关系 不能用一元线性回归模型来描述,所得的回归方程也无意义

(I)F检验法 Q.(n-2) 其中U=∑心,-?(回归平方和) 故F>F-(L,n-2),拒绝H。,否则就接受H。 (Ⅱ)t检验法 当H,成时,T-月1o2 6。 故T>t,。(n-2),拒绝H。,否则就接受Ho 其中L。=∑(x-到2=∑-版
(Ⅰ)F检验法 当 H0 成立时, /( − 2) = Q n U F e ~F(1,n-2) 其中 ( ) = = − n i i U y y 1 2 ˆ (回归平方和) 故 F> (1, 2) F1− n − ,拒绝 H0 ,否则就接受 H0 . (Ⅱ)t 检验法 = = = − = − n i i n i xx i L x x x nx 1 2 2 1 2 其中 ( ) 当 H0 成立时, e Lxx T ˆ ˆ 1 = ~t(n-2) 故 ( 2) 2 1 − − T t n ,拒绝 H0 ,否则就接受 H0