
数学建模与数学实验 无约束最优化
无约束最优化 数学建模与数学实验

实验目的 1.无约束最优化基本算法 2.掌握用数学软件包求解无约束最优化问题. 实验内容 1.无约束优化基本思想及基本算法. 2.MATLAB优化工具箱简介 3.用MATLAB求解无约束优化问题. 4.实验作业
实验目的 实验内容 2.掌握用数学软件包求解无约束最优化问题. 1.无约束最优化基本算法. 1. 无约束优化基本思想及基本算法. 4. 实验作业. 3. 用MATLAB求解无约束优化问题. 2. MATLAB优化工具箱简介

无约束最优化问题 求解无约束最优化问题的的基本思想 *无约束最优化问题的基本算法 返回
无约束最优化问题 求解无约束最优化问题的的基本思想 *无约束最优化问题的基本算法 返回
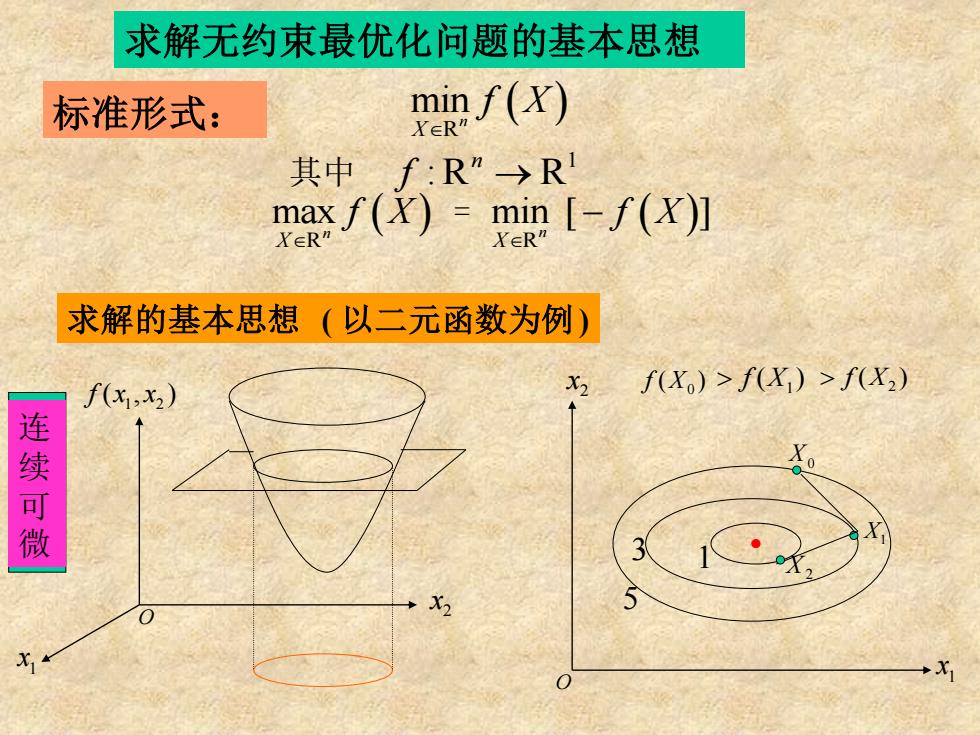
求解无约束最优化问题的基本思想 标准形式: minf(X) XR” 其中 f:R”→R maxf(X)-min[-f(X)月 YER" 求解的基本思想(以二元函数为例) f(x1,x2) X2 f(X)>f(X)>f(X2) 连续可微 X2 X
( ) R min n X f X 其中 1 : R R n f → 标准形式: 求解无约束最优化问题的基本思想 求解的基本思想 ( 以二元函数为例) 1 x 2 x 1 2 f x x ( , ) O 1 x 2 x O 5 3 1 X0 X1 X2 ( ) X0 f ( ) X1 f ( ) X2 f 连 续 可 微 ( ) R max n X f X = ( ) R min [ ] n X f X −
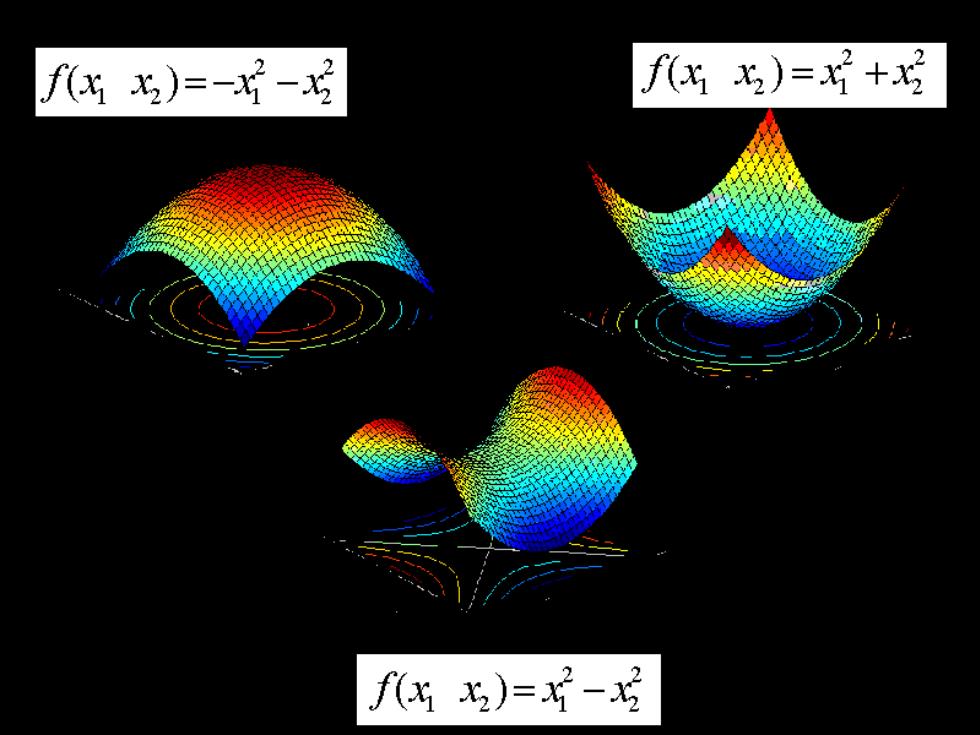
fx为)=-龙-龙 f6龙)=x+x龙 fx为)=片-巧
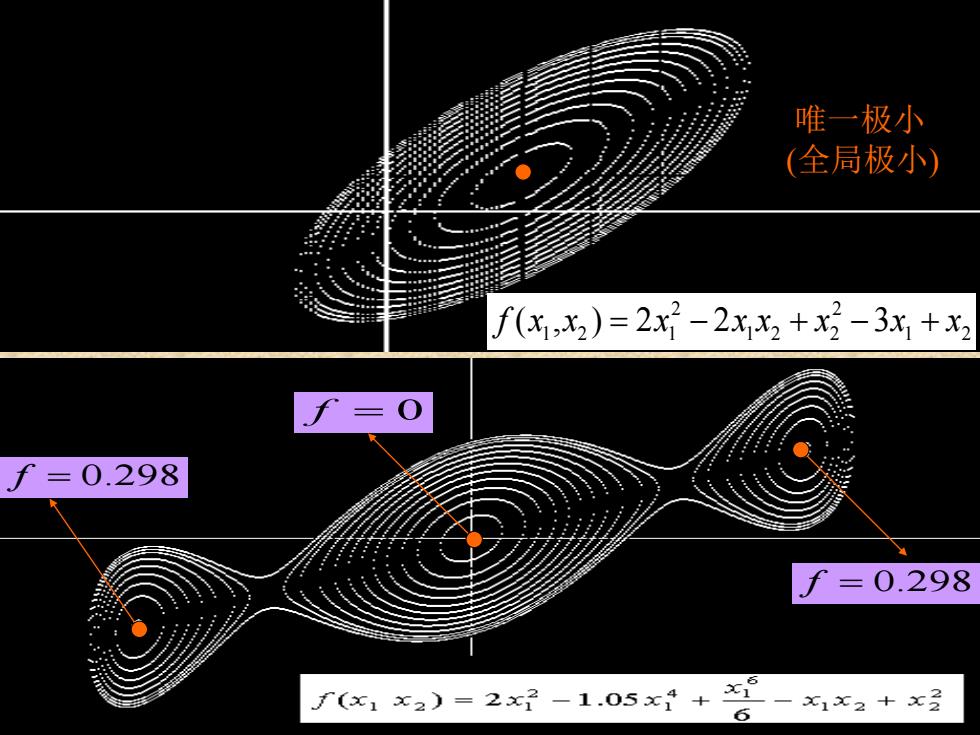
唯一极小 (全局极小) f(x,2)=2x-2xx2+x3-3x+x2 f=0.298 =0.298 f(x1x2)=2x12-1.05x4+ x1 一x1x2+x2
多局部极小 f = 0.298 f = 0 f = 0.298 唯一极小 (全局极小) 2 2 1 2 1 1 2 2 1 2 f x x x x x x x x ( , ) 2 2 3 = − + − +
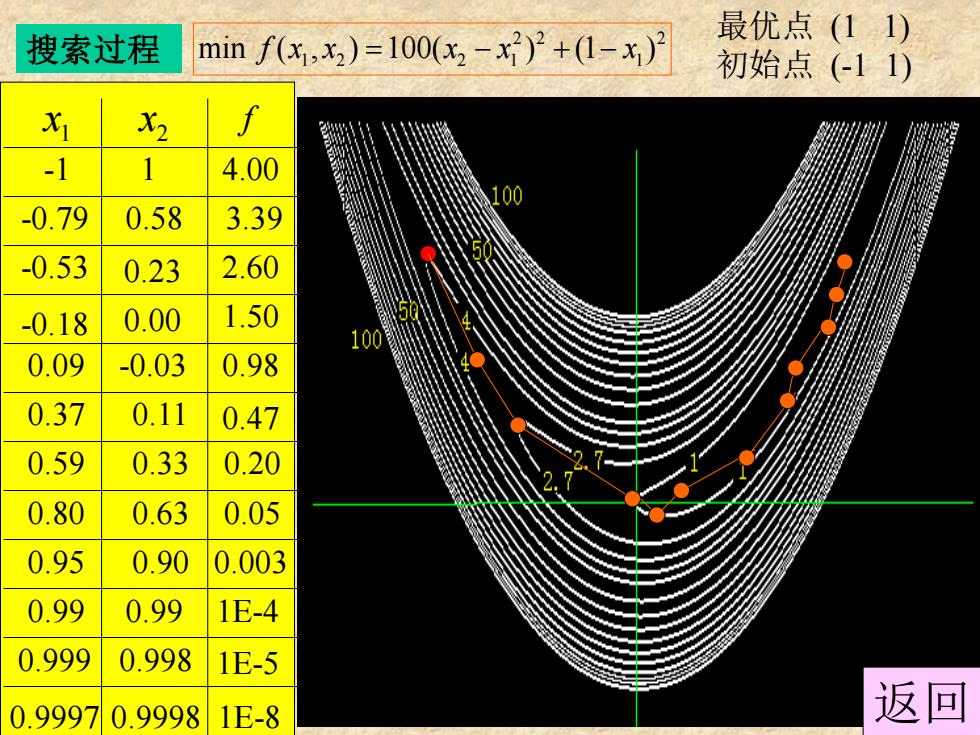
minf(x,x2)=100x2-x2)2+(1-x)月 最优点(11) 搜索过程 初始点(-11) X1 2 -1 1 4.00 -0.79 0.58 3.39 -0.53 0.23 2.60 -0.18 0.00 1.50 100 0.09 -0.03 0.98 0.37 0.11 0.47 0.59 0.33 0.20 0.80 0.63 0.05 0.95 0.90 0.003 0.99 0.99 1E-4 0.999 0.998 1E-5 0.99970.9998 1E-8 返回
搜索过程 2 2 2 min ( , ) 100( ) (1 ) 1 2 2 1 1 f x x x x x = − + − 最优点 (1 1) 初始点 ( -1 1) 1 x 2 x f -1 1 4.00 -0.79 0.58 3.39 -0.53 0.23 2.60 -0.18 0.00 1.50 0.09 -0.03 0.98 0.37 0.11 0.47 0.59 0.33 0.20 0.80 0.63 0.05 0.95 0.90 0.003 0.99 0.99 1E - 4 0.999 0.998 1E - 5 0.9997 0.9998 1E - 8 返回

无约束优化问题的基本算法 1.最速下降法(共轭梯度法)算法步骤: (1)给定初始点X0∈R”,允许误差£>0,令k=0: (2) 计算fX): (3)检验是否满足收敛性的判别准则: fx*≤e, 若满足,则停止迭代,得点X≈X,否则进行(4): (④)令Sk=-fX),从X出发,沿S进行一维搜索, 即求,使得: mnfK*+S)=fx+元,S)月 2>0 (⑤)令X+1=X+元S,K=k+1返回(2). 最速下降法是一种最基本的算法,它在最优化方法中占有重要地位.最 速下降法的优点是工作量小,存储变量较少,初始点要求不高:缺点是收敛 慢,最速下降法适用于寻优过程的前期迭代或作为间插步骤,当接近极值 点时,宜选用别种收敛快的算法
⑴ 给定初始点 0 R n X ,允许误差 0,令 k=0; ⑵ 计算 ( ) k f X ; ⑶ 检验是否满足收敛性的判别准则: ( ) k f X , 若满足,则停止迭代,得点 k X X * ,否则进行⑷; ⑷ 令 ( ) k k S = −f X ,从 k X 出发,沿 k S 进行一维搜索, 即求k ,使得: ( ) ( ) k k k k k f X S f X S + = + 0 min ; ⑸ 令 k k k k X = X + S +1 ,k=k+1 返回⑵. 无约束优化问题的基本算法 最速下降法是一种最基本的算法,它在最优化方法中占有重要地位.最 速下降法的优点是工作量小,存储变量较少,初始点要求不高;缺点是收敛 慢,最速下降法适用于寻优过程的前期迭代或作为间插步骤,当接近极值 点时,宜选用别种收敛快的算法. 1.最速下降法(共轭梯度法)算法步骤:

2.牛顿法算法步骤: (1) 选定初始点X°∈R”,给定允许误差£>0,令0: (2) 求财x),(2fx)'.检验:若fX<ε,则 停止迭代,令X≈X.否则,转(3); (3)令S=-[VfX17fX)(牛顿方向): (4)Xk+1=Xk+S,k=k+1,转回(2). 如果是对称正定矩阵A的二次函数,则用牛顿法,经过一次迭什 就可达到最优点,如不是二次函数,则牛顿法不能一步达到极值点, 但由于这种函数在极值点附近和二次函数很近似,因此牛顿法的收 敛速度还是很快的 牛顿法的收敛速度虽然较快,但要求黑塞矩阵可逆,要计 算二阶导数和逆矩阵,就加大了计算机的计算量和存储量
2.牛顿法算法步骤: (1) 选定初始点 0 R n X ,给定允许误差 0,令 k=0; (2) 求 ( ) k f X , ( ( )) 1 2 − k f X .检验:若 ( ) k f X ,则 停止迭代, * k 令X X .否则, 转(3); (3) 令 ( ) ( ) k k k S = − f X f X 2 −1 [ ] (牛顿方向); (4) k k k X = X + S +1 , k = k +1 ,转回(2). 如果f是对称正定矩阵A的二次函数,则用牛顿法,经过一次迭代 就可达到最优点,如不是二次函数,则牛顿法不能一步达到极值点, 但由于这种函数在极值点附近和二次函数很近似,因此牛顿法的收 敛速度还是很快的. 牛顿法的收敛速度虽然较快,但要求黑塞矩阵可逆,要计 算二阶导数和逆矩阵,就加大了计算机的计算量和存储量

3.拟牛顿法 为克服牛顿法的缺点,同时保持较快收敛速度的优点,利用第k步 和第+1步得到的X,X+,Vf(X),Vf(X+),构造一个正定 矩阵G+近似代替V2f(X),或用H+1近似代替(2f(X),将 牛顿方向改为: G+i Sk=-vf(),Sk+=-HkI Vf() 从而得到下降方向
3.拟牛顿法 为克服牛顿法的缺点,同时保持较快收敛速度的优点,利用第 k 步 和第 k+1 步得到的 k X , k+1 X , ( ) k f X , ( ) +1 k f X ,构造一个正定 矩阵 k +1 G 近似代替 ( ) 2 k f X ,或用 k+1 H 近似代替 2 1 ( ( ))− k f X ,将 牛顿方向改为: k +1 G k +1 S =- ( ) +1 k f X , k +1 S =- k+1 H ( ) +1 k f X 从而得到下降方向