
第三节协方差及相关系数 一、协方差的定义和性质 二、相关系数的定义和性质
一、协方差的定义和性质 二、相关系数的定义和性质 第三节 协方差及相关系数

一、协方差的定义和性质 1.问题的提出 D(X+Y)=D(X)+D(Y)+2E[X-E(X)JY-E(Y)] 若随机变量X与Y相互独立,则E{[X-E(X)[r-E()]}=0, 若E[X-E(X)][Y-E(Y)]≠0,则x与Y不独立,而是存 在一定关系的
一、协方差的定义和性质 若随机变量 X 与 Y 相互独立,则E X E X Y E Y − − = ( ) ( ) 0 . 若E X E X Y E Y − − ( ) ( ) 0 ,则 X 与 Y 不独立,而是存 在一定关系的。 1. 问题的提出 D X Y ( ) + = + D X D Y ( ) ( )+ − − 2 ( ) ( ) E X E X Y E Y

D(X+Y)=D(X)+D(Y)+2EX-E(X)Y-E(Y) 2.定义量EIX-E(X[Y-E(Y)}称为随机变量X与 Y的协方差,记为Cow(X,Y), 即 Cov(X,Y)=E[X-E(X)Y-E(Y) 计算公式:Cow(X,Y)=E(XY)-E(X)E(Y) 】 D(X+Y)=D(X)+D(Y)+2Cov(X,Y) 3.性质 1'Cov(X,Y)=Cov(Y,X),Cov(X,X)=D(X) 2°Cov(aX,bY)=abCov(X,Y)。 3 Cov(Xi+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
即 Cov( , ) ( ) ( ) X Y E X E X Y E Y = − − 。 D( ) D( ) D( ) 2Cov( ) X +Y X Y X,Y = + + ( ) ( ) ( ) ( ) o 1 Cov X,Y Cov Y,X Cov X,X D X = = , 2 o Cov(aX,bY)=abCov(X,Y)。 3 o Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)。 3. 性质 计算公式: Cov , ( X Y E XY E X E Y ) = − ( ) ( ) ( ) 2. 定义 量E X E X Y E Y {[ ( )][ ( )]} − − 称为随机变量 X 与 Y 的协方差,记为Cov( , ) X Y , D X Y ( ) + = + D X D Y ( ) ( ) + − − 2 [ ( )][ ( )] E X E X Y E Y

二、相关系数的定义和性质 ☑引入:CovX,Y)=? Cov(X,Y) I.定义PwDx)NDY西 称为X与Y的相关系数, →Cov(X,Y)=PxyD(X)√D(Y) 注:P灯为无量纲一常数
二、相关系数的定义和性质 Cov( , ) ( ) ( ) X Y XY = Y D X D ρ 1. 定义 Cov( , ) ( ) ( ) XY X Y ρ D X D Y = 称为 X 与 Y 的相关系数. Cov( , )= X Y ? 注:ρXY为无量纲一常数 引入:

2.相关系数的两条性质及含义: 以线性函数a+bX近似表示Y, 其近似程度用均方误差:e=EL(Y-(a+bX)]的大小衡量 问题:求n,b,使e达到最小. e=E[Y-(a+bX)]] =E(Y)+BE(X2)+a2-2bE(XY)+2abE(X)-2aE(Y), ae=2a+2bE(X)-2EY)=0, 令 D e-2bE(x')-2EXY)+2aE(X)=0, 解符A=CoX,a,=E)-EX)ou代” D(X) D(X)
2 2 2 2 = + + − + − E Y b E X a bE XY abE X aE Y ( ) ( ) 2 ( ) 2 ( ) 2 ( ), 2 2 2 ( ) 2 ( ) 0, 2 ( ) 2 ( ) 2 ( ) 0. e a bE X E Y a e bE X E XY aE X b = + − = = − + = 令 解得 0 Cov( , ) , ( ) X Y b D X = 0 Cov( , ) ( ) ( ) . ( ) X Y a E Y E X D X = − 2 e E Y a bX = − + ( ) 以线性函数 a bX Y + 近似表示 , 2 其近似程度用均方误差:e E Y a bX = − + [( ( )) ]的大小衡量. 2. 相关系数的两条性质及含义: 问题:求a b e , ,使 达到最小

将它们代入e=EY-(a+bX)],可得 min E[(Y-(a+bX))2] ,0 =EW-(a,+bX)]=.=(1-Pv2)DY).(参见P107注) min El(Y-(a+bX))2]=El(Y-(ao+b))]=(1-Pxr2)D(Y). 定理:°pxx1 2°pxx=I的充要条件是存在常数a,b使 P(Y=a+bX=1
将它们代入 2 e E Y a bX = − + [( ( )) ],可得 2 , min [( ( )) ] a b E Y a bX − + 2 XY = = − (1 ) ( ). D Y 2 0 0 = − + E Y a b X [( ( )) ] (参见P107注) 定理: 2 2 2 0 0 , 即 min [( ( )) ] [( ( )) ] (1 ) ( ). XY a b E Y a bX E Y a b X D Y − + = − + = − 0 1 1. XY ρ 0 2 1 , ρXY = 的充要条件是存在常数a b使 P Y a bX { } 1 = + =

mine=min El(Y-(a+bX))]=(1-Pxy2)D(Y) a.b ab 说明:P灯是表征X,Y之间线性关系紧密程度的量。 (I)Pxy越大,e越小,表明X与Y的线性关系越紧密。 (2)Py=1时,表明Y与X以概率1存在某种线性关系。 (3)Pxy越小,则X与Y的线性关系越差。 (4)当Px=0时,称X和Y不相关。 不相关的充要条件1°定义:X,Y不相关一P=0; 2°X,Y不相关台Co(X,Y)=0; 3°X,Y不相关台E(XY)=E(X)E(Y) (5)X与Y不相关是就线性关系而言的,相互独立是就一般关系 而言的。 相互独立 一不相关
(2) ρXY =1 时,表明 Y 与 X 以概率 1 存在某种线性关系。 (1) ρXY 越大,e 越小,表明 X 与 Y 的线性关系越紧密。 不相关的充要条件 1 , 0; o 定义:X Y 不相关 = XY o 2 , Cov( , ) 0; X Y X Y 不相关 = o 3 , ( ) ( ) ( ). X Y E XY E X E Y 不相关 = 2 , , min min [( ( )) ] a b a b e E Y a bX = − + 2 XY = − (1 ) ( ). D Y (4)当 XY = 0时, (3) ρXY 越小,则 X 与 Y 的线性关系越差。 说明: 称 X Y 和 不相关。 XY ρ 是表征 X,Y 之间线性关系紧密程度的量。 (5)X 与 Y 不相关是就线性关系而言的,相互独立是就一般关系 而言的。 相互独立 不相关

例1设X与Y的分布律为 YX-2-1 1 2 P(Y=j) 1 01/41/4 0 1/2 4 1/4 00 1/4 1/2 PX=1/41/41/41/4 易知E(X)=0, E(XY)=0, 故Cov(X,Y)=0,Px=0,X与Y不相关。 又P{X=-2,Y=1}=0,PX=-2PY=1=1/8, 则X与Y也不相互独立。 事实上,Y=X2
又 P{X=-2,Y=1}=0, 例 1 设 X 与 Y 的分布律为 Y X -2 -1 1 2 P{Y=j} 1 4 0 1/4 1/4 0 1/4 0 0 1/4 1/2 1/2 P{X=i} 1/4 1/4 1/4 1/4 易知 E(X)=0, 故 Cov(X,Y)=0, X 与 Y 不相关。 则 X 与 Y 也不相互独立。 E(XY)=0, P{X=-2}P{Y=1}=1/8, = 0, XY 事实上,Y=X2

例2设(X,Y)服从二维正态分布,概率密度函数为 nm4i心n2 -1 -, 0102 求X与Y的相关系数。 解:边缘概率密度分别为 x-4)2 Jx(x)= 21 (-∞<x<∞), √2π01 y-22 1ea好 f0)-26, (-0<y<∞)
例2 设(X,Y)服从二维正态分布,概率密度函数为 2 1 2 1 ( , ) exp 2 1 f x y σ σ ρ = − 2 1 2(1 ) ρ − − 2 2 1 1 2 2 2 2 1 2 1 2 ( ) ( )( ) ( ) 2 x μ x μ y μ y μ ρ σ σ σ σ − − − − − + 求 X 与 Y 的相关系数。 解:边缘概率密度分别为 2 1 2 1 ( ) 2 1 1 ( ) ( ), 2 x μ σ X f x e x σ − − = − 2 2 2 2 ( ) 2 2 1 ( ) ( ). 2 y μ σ Y f y e y σ − − = −
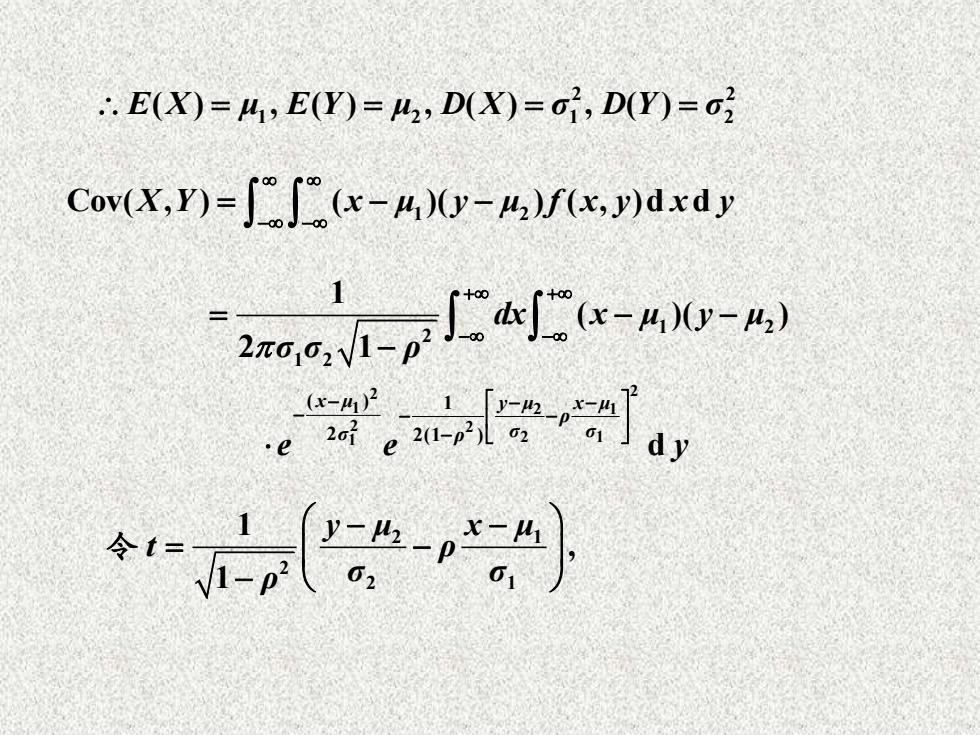
.E(X)=41,E(Y)=2,D(X)=o1,D(Y)=o2 Cov(X,Y)=∫∫(x-40y-Afx,)dxdy mA-k-4 2-}
2 2 1 2 1 2 = = = = E X( ) , ( ) , ( ) , ( ) μ E Y μ D X σ D Y σ Cov( , ) ( )( ) ( , )d d X Y x μ1 2 y μ f x y x y − − = − − 2 2 1 2 1 2 2 1 2 1 1 2 2 1 2 ( ) 1 2 2(1 ) 1 ( )( ) 2 1 d x μ y μ x μ ρ σ ρ σ σ dx x μ y μ σ σ ρ e e y + + − − − − − − − − − = − − − 2 1 2 2 1 1 , 1 y μ x μ t ρ ρ σ σ − − = − − 令