
数学建模与数学实验 数据的统计描述和分析
数学建模与数学实验 数据的统计描述和分析

实验目的 1.直观了解统计基本内容 2.掌握用数学软件包求解统计问题 卖验内容 1.统计的基本理论. 2.用数学软件包求解统计问题 3.实验作业
实验目的 实验内容 2.掌握用数学软件包求解统计问题. 1.直观了解统计基本内容. 1.统计的基本理论. 3.实验作业. 2.用数学软件包求解统计问题
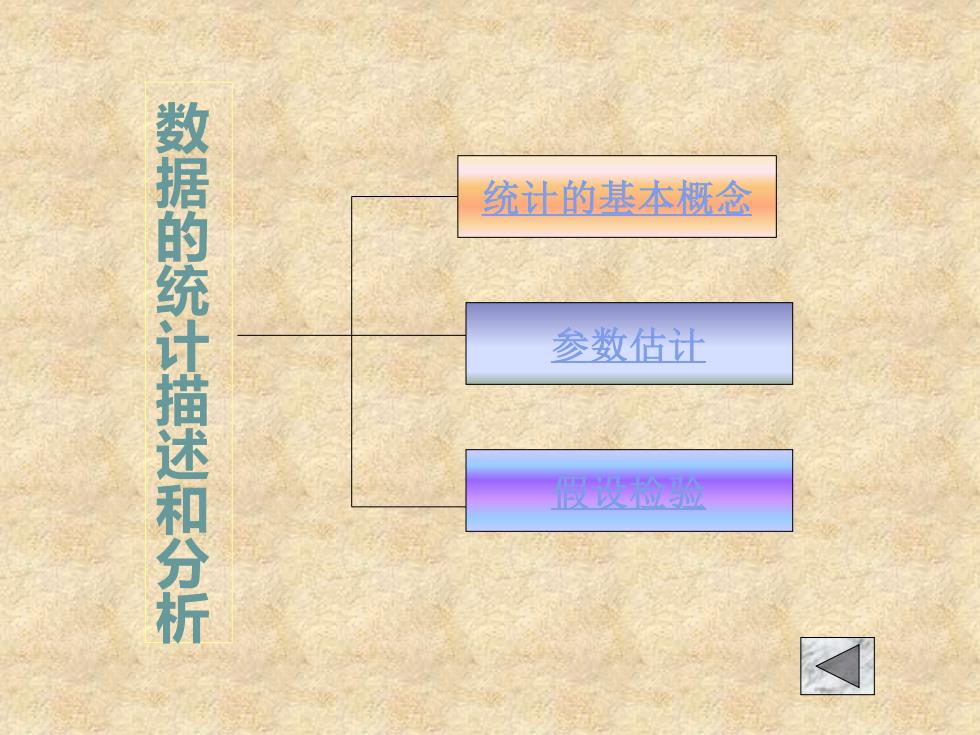
数据的统计描述和分析 统计的基本概念 参数估计 假发验
统计的基本概念 参数估计 假设检验 数据的统计描述和分析
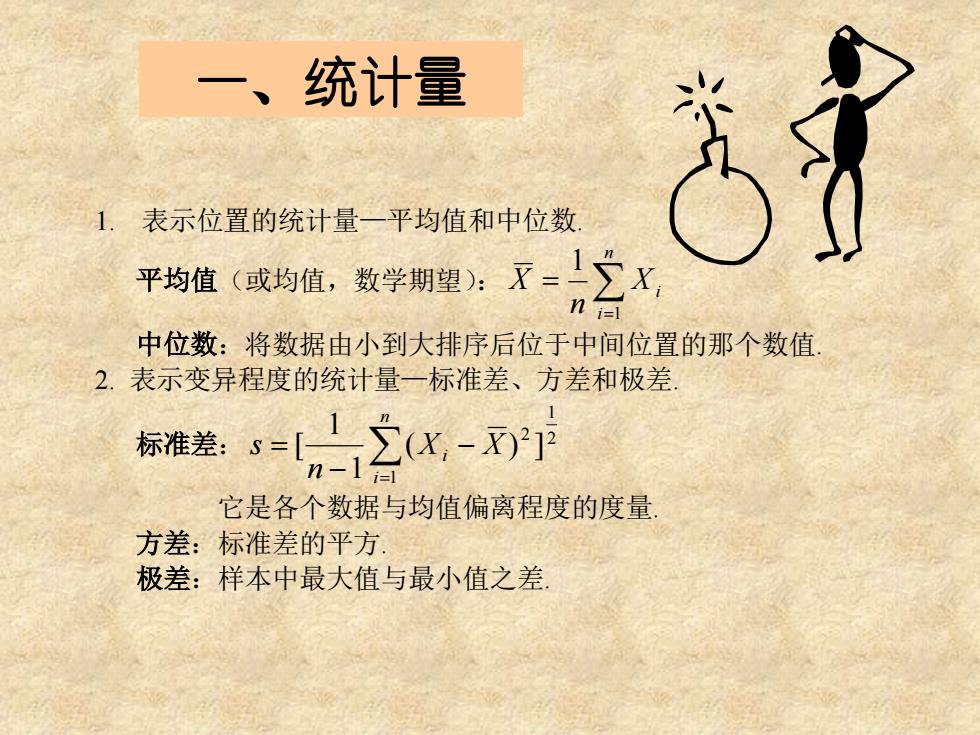
一、统计量 1. 表示位置的统计量一平均值和中位数 7 平均值(或均值,数学期望):刀=∑X n i= 中位数:将数据由小到大排序后位于中间位置的那个数值 2.表示变异程度的统计量一标准差、方差和极差 标准差,三(X小 它是各个数据与均值偏离程度的度量 方差:标准差的平方 极差:样本中最大值与最小值之差
1. 表示位置的统计量—平均值和中位数. 平均值(或均值,数学期望): = = n i Xi n X 1 1 中位数:将数据由小到大排序后位于中间位置的那个数值. 2. 表示变异程度的统计量—标准差、方差和极差. 标准差: 2 1 1 2 ( ) ] 1 1 [ = − − = n i Xi X n s 它是各个数据与均值偏离程度的度量. 方差:标准差的平方. 极差:样本中最大值与最小值之差. 一、统计量

3.表示分布形状的统计量一偏度和峰度 偏度:8=号2X-X0降度::2(x-对 偏度反映分布的对称性,g1>0称为右偏态,此时数据位于均值 右边的比位于左边的多;g1<0称为左偏态,情况相反:而g1接近0 则可认为分布是对称的 峰度是分布形状的另一种度量,正态分布的峰度为3,若g2比3 大很多,表示分布有沉重的尾巴,说明样本中含有较多远离均值的数 据,因而峰度可用作衡量偏离正态分布的尺度之一 4k阶原点矩:y=1∑Xk阶中心矩:U,=1∑(X,-X) n i=l ni=
3. 表示分布形状的统计量—偏度和峰度 偏度: = = − n i Xi X s g 1 3 1 3 ( ) 1 峰度: = = − n i Xi X s g 1 4 2 4 ( ) 1 偏度反映分布的对称性,g1 >0 称为右偏态,此时数据位于均值 右边的比位于左边的多;g1 <0 称为左偏态,情况相反;而 g1接近 0 则可认为分布是对称的. 峰度是分布形状的另一种度量,正态分布的峰度为 3,若 g2比 3 大很多,表示分布有沉重的尾巴,说明样本中含有较多远离均值的数 据,因而峰度可用作衡量偏离正态分布的尺度之一. 4. k 阶原点矩: = = n i k k Xi n V 1 1 k 阶中心矩: = = − n i k k Xi X n U 1 ( ) 1

二、分布函数的近似求法 1整理资料:把样本值x1,2,.,xn进行分组,先将它们依大小次序排列, 得x≤x2≤.≤x,在包含[x,x]的区间[a,b]内插入一些等分点: a<x<x2<.<x,<b,注意要使每一个区间(x,x](=1,2,.,n-1) 内都有样本观测值x(=1,2,.,-1)落入其中 2.求出各组的频数和频率:统计出样本观测值在每个区间(x,x]中出 现的次数口,它就是这区间或这组的频数计算频率f= n 3作频率直方图:在直角坐标系的横轴上,标出x,x2,.,xn各点,分别以 (x,x]为底边,作高为的矩形,△x=x1-x,1=1,2,n-1,即得 △X 频率直方图
二、分布函数的近似求法 1.整理资料: 把样本值 x1,x2,.,xn进行分组,先将它们依大小次序排列, 得 * * 2 * 1 n x x x .在包含[ , ] * * 1 n x x 的区间[a,b]内插入一些等分点: , ' ' 2 ' a x1 x xn b 注意要使每一个区间( , ] ' 1 ' i i+ x x (i=1,2,.,n-1) 内都有样本观测值 xi(i=1,2,.,n-1)落入其中. 2.求出各组的频数和频率:统计出样本观测值在每个区间( , ] ' 1 ' i i+ x x 中出 现的次数 i n ,它就是这区间或这组的频数.计算频率 n n f i i = . 3.作频率直方图:在直角坐标系的横轴上,标出 ' ' 2 ' 1 , , , n x x x 各点,分别以 ( , ] ' 1 ' i i+ x x 为底边,作高为 ' i i x f 的矩形, , 1,2, , 1 ' ' 1 ' xi = xi+ − xi i = n − ,即得 频率直方图
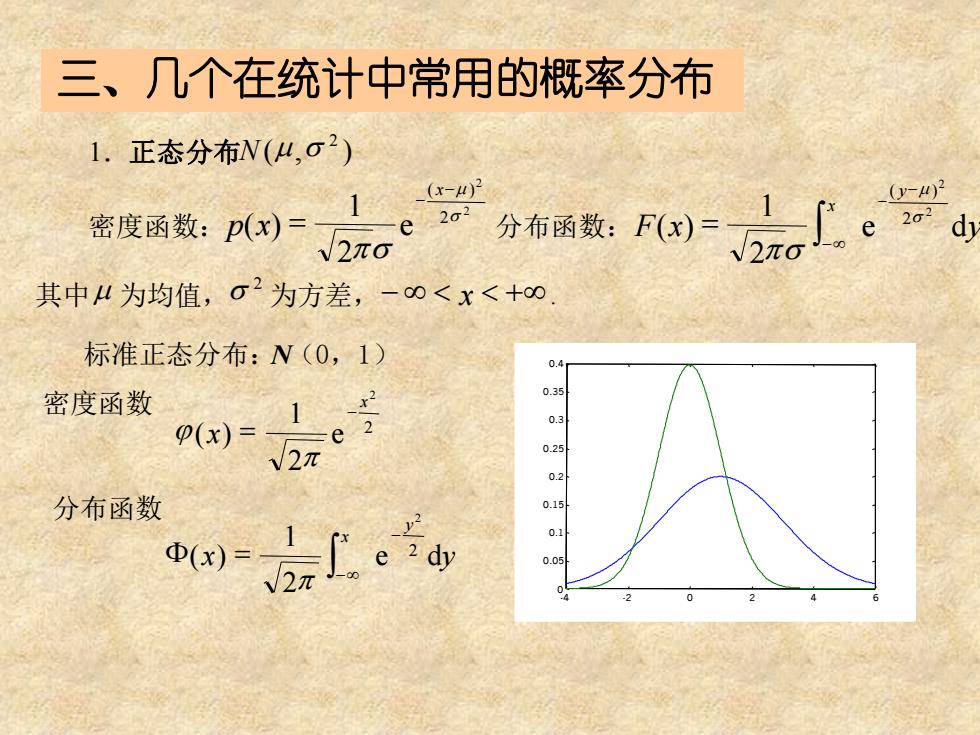
三、几个在统计中常用的概率分布 1.正态分布N(4,o2) 1 (x-4)2 (y-4)2 密度函数:p(x)= √2πo 其中4为均值,σ2为方差,-0<x<+o0 标准正态分布:N(0,1) 0.4 密度函数 0.35 p(x)= W2π 0 分布函数 Φ(x)= 4
三、几个在统计中常用的概率分布 -4 -2 0 2 4 6 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 1.正态分布 ( , ) 2 N m s 密度函数: 2 2 2 ( ) 2 1 ( ) s m ps − − = x p x e 分布函数:F x e dy y x 2 2 2 ( ) 2 1 ( ) s m ps − − − = 其中m 为均值, 2 s 为方差,− x +. 标准正态分布:N(0,1) 密度函数 2 2 2 1 ( ) x x e − = p j x e dy y x 2 2 2 1 ( ) − − F = p 分布函数

2.X2分布x2() 若随机变量X1,X2,.,Xn相互独立,都 服从标准正态分布N(0,1),则随机变量 Y=Xi+X2++X2 服从自由度为n的x2分布,记为Y~x2(n). Y的均值为n,方差为2n 校
0 5 10 15 20 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 2. 2 分布 2 (n) 若随机变量 X1,X2,.,Xn 相互独立,都 服从标准正态分布 N(0,1),则随机变量 Y= 2 2 2 2 X1 + X ++ Xn 服从自由度为 n 的 2 分布,记为 Y~ 2 (n). Y 的均值为 n,方差为 2n
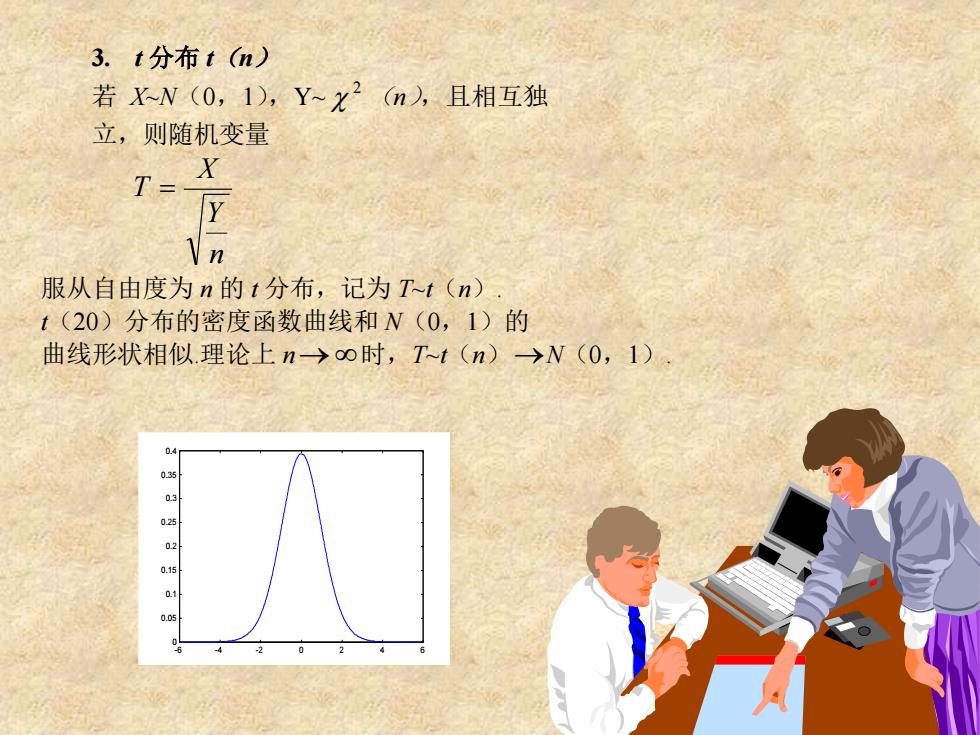
3.t分布tn) 若X~N(0,1),Y~X2(n,且相互独 立,则随机变量 T=_Y n 服从自由度为n的t分布,记为T~t(n) t(20)分布的密度函数曲线和N(0,1)的 曲线形状相似.理论上n→o时,Tt(n)→N(0,1), 0.0s
3. t 分布 t(n) 若 X~N(0,1),Y~ 2 (n),且相互独 立,则随机变量 n Y X T = 服从自由度为 n 的 t 分布,记为 T~t(n). t(20)分布的密度函数曲线和 N(0,1)的 曲线形状相似.理论上 n→ 时,T~t(n)→N(0,1). -6 -4 -2 0 2 4 6 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
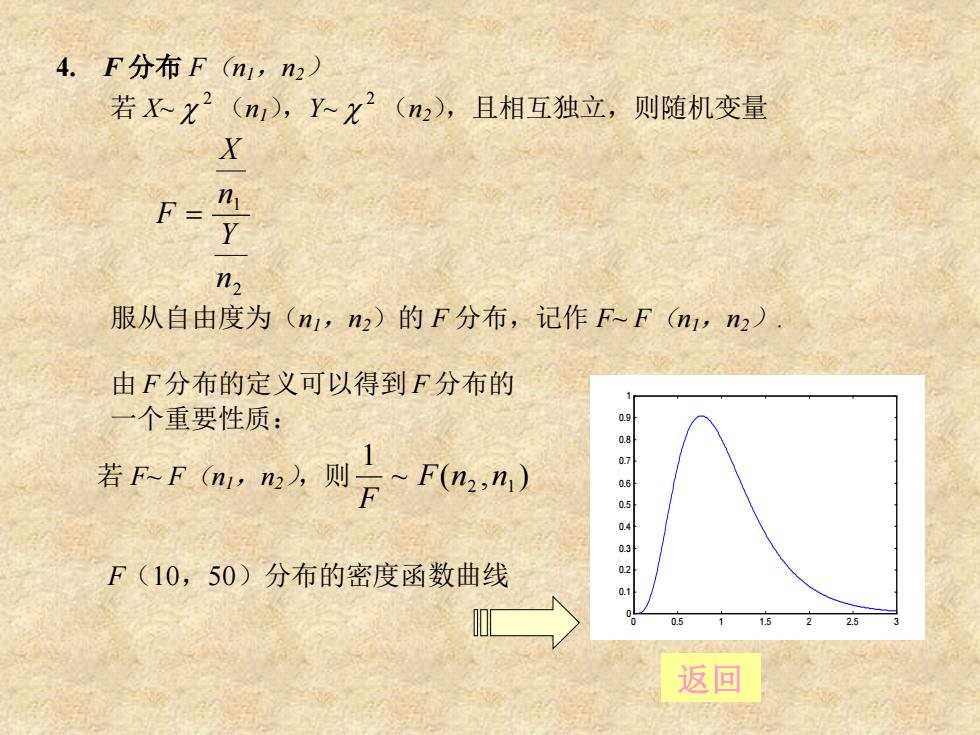
4.F分布F(n,n2) 若Xx2(m),Yx2(n2),且相互独立,则随机变量 X 九 F= n2 服从自由度为(n1,n2)的F分布,记作F~F(n1,n2) 由F分布的定义可以得到F分布的 一个重要性质: 若rFm,则Fmn) 9订65432 F(10,50)分布的密度函数曲线 0 0.5 2.5 返回
4. F 分布 F(n1,n2) 若 X~ 2 (n1),Y~ 2 (n2),且相互独立,则随机变量 2 1 n Y n X F = 服从自由度为(n1,n2)的 F 分布,记作 F~ F(n1,n2). 由 F 分布的定义可以得到 F 分布的 一个重要性质: 若 F~ F(n1,n2),则 ~ ( , ) 1 F n2 n1 F 0 0.5 1 1.5 2 2.5 3 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 返回 F(10,50)分布的密度函数曲线