
《数学建模与数学实验》实验指导书 《数学建模与数学实验》实验指导书 基础实验一:matlab程序设计与作图 实验目的 熟悉MATLAB软件的用户环境:了解MATLAB软件的一般命令:掌握MATLAB向 量、数组、矩阵操作与运算函数:掌握MATLAB软件的基本绘图命令:掌握MATLAB语 言的几种循环、条件和开关选择结构,及其编程规范。 通过该实验的学习,使学生能灵活应用MATLAB软件解决一些荷单问题,能借助 MATLAB软件的绘图功能,对函数的特性进行探讨,广泛联想,大胆猜想,发现进而证实 其中的规律。 实验内容 1.MATLAB软件的数组操作及运算练习: 2.直接使用MATLAB软件进行作图练习: 3.用MATLAB语言编写命令M文件和函数M文件 实验步臻 1.在D盘建立一个自己的文件夹: 2.开启软件平台一MATLAB,将你建立的文件夹加入到MATLAB的搜素路径中: 3.利用帮助了解函数max,min,sum,mean,sort,.length,rand,size和diag的功能和用 法: 4.开启MATLAB编辑窗口,键入你编写的M文件(命令文件或函数文件): 5.保存文件(注意将文件存入你自己的文件夹)并运行: 6.若出现错误,修改、运行直到输出正确结果 7.写出实验报告,并浅谈学习心得体会。 实验要求与任务 根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的一问题一算 法与编程一→计算结果或图形→心得体会) 「3117 「11-1 1.已知矩阵A=212,B=2-10 123 101 第1页
《数学建模与数学实验》实验指导书 第1页 《数学建模与数学实验》实验指导书 基础实验一:matlab 程序设计与作图 实验目的 熟悉 MATLAB 软件的用户环境;了解 MATLAB 软件的一般命令;掌握 MATLAB 向 量、数组、矩阵操作与运算函数;掌握 MATLAB 软件的基本绘图命令;掌握 MATLAB 语 言的几种循环、条件和开关选择结构,及其编程规范。 通过该实验的学习,使学生能灵活应用 MATLAB 软件解决一些简单问题,能借助 MATLAB 软件的绘图功能,对函数的特性进行探讨,广泛联想,大胆猜想,发现进而证实 其中的规律。 实验内容 1.MATLAB 软件的数组操作及运算练习; 2.直接使用 MATLAB 软件进行作图练习; 3.用 MATLAB 语言编写命令 M 文件和函数 M 文件。 实验步骤 1.在 D 盘建立一个自己的文件夹; 2.开启软件平台——MATLAB,将你建立的文件夹加入到 MATLAB 的搜索路径中; 3.利用帮助了解函数 max, min, sum, mean, sort, length,rand, size 和 diag 的功能和用 法; 4.开启 MATLAB 编辑窗口,键入你编写的 M 文件(命令文件或函数文件); 5.保存文件(注意将文件存入你自己的文件夹)并运行; 6.若出现错误,修改、运行直到输出正确结果; 7.写出实验报告,并浅谈学习心得体会。 实验要求与任务 根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→算 法与编程→计算结果或图形→心得体会) 1. 已知矩阵 = 1 2 3 2 1 2 3 1 1 A , − − = 1 0 1 2 1 0 1 1 1 B

《数学建模与数学实验》实验指导书 要求:(1)屏幕输出A与B:(2)A的转置A:(3)求A+B的值:(4)求A-B的值:(5) 求4A:(6)求A×B:(7)求A. 2.有一函数xy=2+si0+2,写一程序,输入自变量的值,输出函数值。 3.用plot,fplot分别绘制函数=cos(tan(元x》图形 4绘制函数r=a1-sm ly=a(1-cos' 在1e[0,2]上的图形。 5.作出下列曲面的三维图形: x=(1+cosu)cosv, y=(1+cosu)sin v, z=sin u. ue(0,2π,ve(0,2) 6.建立一个M文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其 各位数字的立方和等于该数本身。例如:153是一个水仙花数,因为153=13+53+3。 A=0: a=fix(x/100)b-fix(x-a*100)/10),c=xa*100-b*10 ifx==a^3+b3+c3 A=[A.x] end end disp(A) 基础实验二:matlab函数拟合 实验目的:掌握用matlab进行函数拟合的方法。 实验内容: 根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型 (L0 gistic模型)中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。 表!美国人口统计数据 第2项
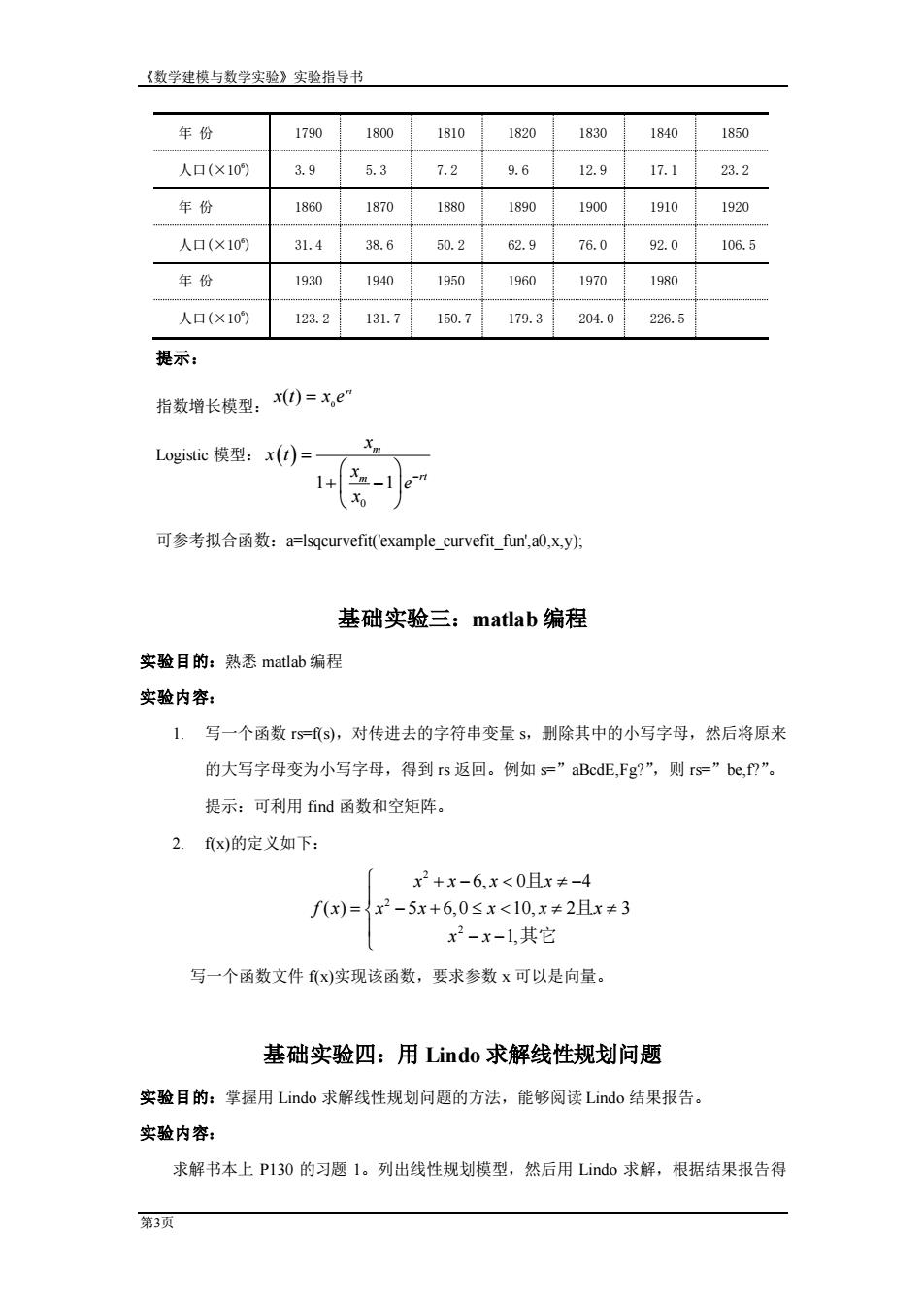
《数学建模与数学实验》实验指导书 第2页 要求:(1)屏幕输出 A 与 B;(2)A 的转置 A′;(3)求 A+B 的值;(4)求 A-B 的值;(5) 求 4A;(6)求 A×B;(7)求 A-1. 2. 有一函数 f(x,y)=x 2+sinxy+2y,写一程序,输入自变量的值,输出函数值。 3. 用 plot,fplot 分别绘制函数 y=cos(tan( x))图形。 4. 绘制函数 = − = − (1 cos ) ( sin ) 3 3 y a t x a t t 在 t [0,2 ] 上的图形。 5. 作出下列曲面的三维图形: = = + = + (0,2 ), (0,2 ) sin , (1 cos )sin , (1 cos ) cos , u v z u y u v x u v 6.建立一个 M 文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其 各位数字的立方和等于该数本身。例如:153 是一个水仙花数,因为 153=13+53+33。 A=[]; a=fix(x/100);b=fix((x-a*100)/10);c=x-a*100-b*10; if x==a^3+b^3+c^3 A=[A,x]; end end disp(A) 基础实验二:matlab 函数拟合 实验目的:掌握用 matlab 进行函数拟合的方法。 实验内容: 根据美国人口从 1790 年到 1990 年间的人口数据(如下表),确定人口指数增长模型 (Logistic 模型)中的待定参数,估计出美国 2010 年的人口,同时画出拟合效果的图形。 表 1 美国人口统计数据
《数学建模与数学实验》实验指导书 年份 1790 1800 1810 1820 1830 1840 1850 人口(×10) 3.9 5.3 7.2 9.6 12.9 17.123.2 年份 1860 1870 1880 1890 1900 1910 1920 人口(×10 31.4 38.6 50.2 62.976.0 92.0 106.5 年份 1930 1940 1950 1960 1970 1980 人口(×10 123.2 131.7 150.7 179.3 204.0 26.5 提示: 指数增长模型:0=x,e Logistic模型:x()= +-le x月 可参考拟合函数:a=-lsqcurvefit(example_curvefit_fun,aO,xy 基础实验三:matlab编程 实验目的:熟悉matlab编程 实验内容: 1.写一个函数SS),对传进去的字符串变量s,删除其中的小写字母,然后将原来 的大写字母变为小写字母,得到rs返回。例如s=”aBcd正,Fg?”,则rs”be,f?”。 提示:可利用find函数和空矩阵。 2.fx)的定义如下: x2+x-6,x<0且x≠-4 f(x)={x2-5x+6,0≤x<10,x≠2且x≠3 x2-x-1其它 写一个函数文件x实现该函数,要求参数x可以是向量。 基础实验四:用Lindo求解线性规划问题 实验目的:掌握用Lindo求解线性规划问题的方法,能够阅读Lindo结果报告。 实验内容: 求解书本上PI30的习题l。列出线性规划模型,然后用Lido求解,根据结果报告得 第3项
《数学建模与数学实验》实验指导书 第3页 年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106 ) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106 ) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106 ) 123.2 131.7 150.7 179.3 204.0 226.5 提示: 指数增长模型: rt x t x e0 ( ) = Logistic 模型: ( ) 0 1 1 m m rt x x t x e x − = + − 可参考拟合函数:a=lsqcurvefit('example_curvefit_fun',a0,x,y); 基础实验三:matlab 编程 实验目的:熟悉 matlab 编程 实验内容: 1. 写一个函数 rs=f(s),对传进去的字符串变量 s,删除其中的小写字母,然后将原来 的大写字母变为小写字母,得到 rs 返回。例如 s=”aBcdE,Fg?”,则 rs=”be,f?”。 提示:可利用 find 函数和空矩阵。 2. f(x)的定义如下: 2 2 2 6, 0 4 ( ) 5 6,0 10, 2 3 1, x x x x f x x x x x x x x + − − = − + − − 且 且 其它 写一个函数文件 f(x)实现该函数,要求参数 x 可以是向量。 基础实验四:用 Lindo 求解线性规划问题 实验目的:掌握用 Lindo 求解线性规划问题的方法,能够阅读 Lindo 结果报告。 实验内容: 求解书本上 P130 的习题 1。列出线性规划模型,然后用 Lindo 求解,根据结果报告得

《数学建模与数学实验》实验指导书 出解决方案。 提示: 模型可以如下建立: 设投资证券A,B,C,D,E的金额分别为x1,x2,x3,x4x5万元 max0.043x1+0.027x2+0.025x3+0.022x4+0.045x5 x2+x3+X4>=400 x1+x2+x3+x4+x5”与“=”功能相同 2.变量与系数间可有空格(甚至回车),但无运算符 3.变量以字母开头,不能超过8个字符 4.变量名不区分大小写(包括关健字) 5.目标函数所在行是第一行,第二行起为约束条件 6.行号自动产生或人为定义,以“)”结束 7.“1”后为注释。 8.在模型任何地方都可以用“TTE”对模型命名 9.变量不能出现在一个约束条件的右端 10.表达式中不接受括号和逗号等符号 .表达式应化简,如2x1+3x2-4x1应写成-2x1+3x2 l2.缺省假定所有变量非负,可在模型“END”语句后用“FREE name'”将变量name的非 负假定取消 13.可在“END”后用“SUB”或“SLB”设定变量上下界。例如:“bx110”表示“x1<10” 14.“END”后对O-l变量说明:INTn或INT name 15.“END”后对整数变量说明:GINn或GIN name 基础实验五:用Lingo求解非线性规划问题 实验目的:掌握用Ligo求解非线性规划问题的方法。 第4页
《数学建模与数学实验》实验指导书 第4页 出解决方案。 提示: 模型可以如下建立: 设投资证券 A,B,C,D,E 的金额分别为 x1,x2,x3,x4,x5 万元. max 0.043x1+0.027x2+0.025x3+0.022x4+0.045x5 x2+x3+x4>=400 x1+x2+x3+x4+x5”与“>=”功能相同 2. 变量与系数间可有空格(甚至回车),但无运算符 3. 变量以字母开头,不能超过 8 个字符 4. 变量名不区分大小写(包括关键字) 5. 目标函数所在行是第一行,第二行起为约束条件 6. 行号自动产生或人为定义,以“)”结束 7. “!”后为注释。 8. 在模型任何地方都可以用“TITLE”对模型命名 9. 变量不能出现在一个约束条件的右端 10. 表达式中不接受括号和逗号等符号 11. 表达式应化简,如 2x1+3x2-4x1 应写成-2x1+3x2 12. 缺省假定所有变量非负,可在模型“END”语句后用“FREE name”将变量 name 的非 负假定取消 13. 可在“END”后用“SUB”或“SLB”设定变量上下界。例如:“sub x1 10”表示“x1<=10” 14. “END”后对 0-1 变量说明:INT n 或 INT name 15. “END”后对整数变量说明:GIN n 或 GIN name 基础实验五:用 Lingo 求解非线性规划问题 实验目的:掌握用 Lingo 求解非线性规划问题的方法

《数学建模与数学实验》实验指导书 实验内容: 求解书本上P132的习题7。列出非线性规划模型,然后用Lig0求解,根据结果报告 得出解决方案。 提示 可参考书上钢管切割模型的例子,注意有所修改。比如目标函数应该为: m1n=(x1+0.1)*y1+(x2+0.2)*y2+(x3+0.3)*y3+(x4+0.4)*y4; y1,y2,y3,y4是0-1变量。 约束条件可为: x1*r11+x2*r12+x3*r13+x4*r14>=15;。·。 290*r11+315*x21+350*r31+455*r41-19: x1<-y1*100:·。· 基础实验六:用Lingo求解大规模线性规划问题 实验目的:掌握用Ligo求解大规模线性规划问题的方法。 实验内容: 求解全国大学生数学建模竞赛O5年B题问题2:DVD的分配。会员每次租赁3张DVD,现 在给出网站手上的100种DVD的现有张数和当前需要处理的1000位会员的在线订单,如何对 这些DVD进行分配,才能使会员获得最大的满意度? 现有DVD张数和当前需要处理的会员的在线订单(表格格式示例 DVD编号 D001 D002 D003 D004 DVD现有数量 10 40 15 20 C0001 会员 C0002 0 在线 C0003 钉单 C0004 第5页
《数学建模与数学实验》实验指导书 第5页 实验内容: 求解书本上 P132 的习题 7。列出非线性规划模型,然后用 Lingo 求解,根据结果报告 得出解决方案。 提示: 可参考书上钢管切割模型的例子,注意有所修改。比如目标函数应该为: min =(x1+0.1)*y1+(x2+0.2)*y2+(x3+0.3)*y3+(x4+0.4)*y4; y1,y2,y3,y4是0-1变量。 约束条件可为: x1*r11+x2*r12+x3*r13+x4*r14>=15; 。 290*r11+315*r21+350*r31+455*r41=19; x1<=y1*100; 。 基础实验六:用 Lingo 求解大规模线性规划问题 实验目的:掌握用 Lingo 求解大规模线性规划问题的方法。 实验内容: 求解全国大学生数学建模竞赛05年B题问题2:DVD的分配。会员每次租赁3张DVD,现 在给出网站手上的100种DVD的现有张数和当前需要处理的1000位会员的在线订单,如何对 这些DVD进行分配,才能使会员获得最大的满意度? 现有 DVD 张数和当前需要处理的会员的在线订单(表格格式示例) DVD 编号 D001 D002 D003 D004 . DVD 现有数量 10 40 15 20 . 会员 在线 订单 C0001 6 0 0 0 . C0002 0 0 0 0 . C0003 0 0 0 3 . C0004 0 0 0 0 . . . . . .

《数学建模与数学实验》实验指导书 注:D001~D100表示100种DVD,C0001-C1000表示1000个会员,会员的在线订单用数字 1,2.表示,数字越小表示会员的偏爱程度越高,数字0表示对应的DVD当前不在会员的在 线订单中。所有数据将可从htp:lmcm.edu.cn/mcmO5/problems2.005c.asp下载。 提示: 可建立如下0-1规划模型: m:-2 空,-J-2m st: <=3.j=12.,1000 x=0或1, 1,j=1,2.,n 其中c可是偏爱指数,其中0改成1,其他数字如果是c,则用1c代替。 可参考如下运输问题代码: model: 6发点8收点运输问 sets: warehouses/wh1.wh6/:capacity: vendors/v1.v8/:demand: links(warehouses,vendors):cost,volume endsets !目标函数 min=esum(links:costvolume) !需求约束: efor(vendors(J): @sum(warehouses(I):volume(I,J))=demand(J)): 产量约束 @for(warehouses(I): @sum(vendors(I):volume(I.I))<=capacity(1)) 这里是数据 data: capacity=605551434152: 第6页
《数学建模与数学实验》实验指导书 第6页 注:D001~D100表示100种DVD, C0001~C1000表示1000个会员, 会员的在线订单用数字 1,2,.表示,数字越小表示会员的偏爱程度越高,数字0表示对应的DVD当前不在会员的在 线订单中。所有数据将可从http://mcm.edu.cn/mcm05/problems2005c.asp下载。 提示: 可建立如下 0-1 规划模型: 1000 100 , , 1 1 1000 , 1 100 , 1 , max * , 1, 2, ,100 : 3, 1, 2, ,1000 0 1, , 1, 2, , i j i j i j i j j i i j j i j z c x x N j st x j x i j n = = = = = = = = = = = 或 其中 cij 是偏爱指数,其中 0 改成-1,其他数字如果是 c,则用 11-c 代替。 可参考如下运输问题代码: model: !6 发点 8 收点运输问题; sets: warehouses/wh1.wh6/: capacity; vendors/v1.v8/: demand; links(warehouses,vendors): cost, volume; endsets !目标函数; min=@sum(links: cost*volume); !需求约束; @for(vendors(J): @sum(warehouses(I): volume(I,J))=demand(J)); !产量约束; @for(warehouses(I): @sum(vendors(J): volume(I,J))<=capacity(I)); !这里是数据; data: capacity=60 55 51 43 41 52;

《数学建模与数学实验》实验指导书 demand=3537223241324338: cost=62674295 49538582 52197433 76739271 23957265 55228143: enddata end 基础实验七:用matlab求解微分方程(组) 实验目的:掌握用matlab求微分方程和微分方程组的数值解的方法。 实验内容: 求解书上P138,P139页的微分方程和微分方程组,画出书中图3、4、5、6、7、8。 提示: 要求解微分方程(组)dydt=L,y),可如下调用: [T.Y]-ode45(f.[t0,tn].y0) 1.函数在求解区间O,m内,自动设立采样点向量T,并求出解函数y在采样点T处的样 本值Y。 2.「是一个函数,要有两个参数,第一个参数是自变量t,第二个参数是因变量y。 3.y0y(0)给定方程的初值。 例:求微分方程初值问题dy/dx=-2yx+4x,y(1)=2在[1,3]区间内的数值解,并将结果与解 析解进行比较。 先建立一个该函数的m文件yl.m: function f=f(x.y) f-2.y.k+4x %注意使用点运算符 再输入命令: [X,Y门=ode45(fy1,[1,3],2 %显示自变量的一组采样点 %显示求解函数与采样点对应的一组数值解 第7页
《数学建模与数学实验》实验指导书 第7页 demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 5 4 9 5 3 8 5 8 2 5 2 1 9 7 4 3 3 7 6 7 3 9 2 7 1 2 3 9 5 7 2 6 5 5 5 2 2 8 1 4 3; enddata end 基础实验七:用 matlab 求解微分方程(组) 实验目的:掌握用 matlab 求微分方程和微分方程组的数值解的方法。 实验内容: 求解书上 P138,P139 页的微分方程和微分方程组,画出书中图 3、4、5、6、7、8。 提示: 要求解微分方程(组)dy/dt=f(t,y),可如下调用: [T,Y]=ode45(f,[t0,tn],y0) 1. 函数在求解区间[t0,tn]内,自动设立采样点向量 T,并求出解函数 y 在采样点 T 处的样 本值 Y。 2. f 是一个函数,要有两个参数,第一个参数是自变量 t,第二个参数是因变量 y。 3. y0=y(t0)给定方程的初值。 例:求微分方程初值问题 dy/dx=-2y/x+4x,y(1)=2 在[1,3]区间内的数值解,并将结果与解 析解进行比较。 先建立一个该函数的 m 文件 fxy1.m: function f=f(x,y) f=-2.*y./x+4*x %注意使用点运算符 再输入命令: [X,Y]=ode45('fxy1',[1,3],2); X' %显示自变量的一组采样点 Y' %显示求解函数与采样点对应的一组数值解

《数学建模与数学实验》实验指导书 (X2+1.X2y %显示求解函数与采样点对应的一组解析解 例:求解常微分方程组初值问题在区间0,2)中的解。 dv. ,(0)=5 =-xy2+x2-5,y,(0)=6 I dx 建立一个函数文件6y2.m: function f=fxy) f1)y(2: f2=-xy(2)+x2-5 f-f: 在MATLAB命令窗口,输入命令: [X,Y-ode45(fy2,0,21.[5,6 基础实验八:matlab数值计算 实验目的:掌握用matlab进行插值、拟合、方程求解等数值计算的方法。 实验内容: 1,某气象观测站测得某日6:00-18:00之间每隔2小时的温度如下: 试用三次样条插值求出该日630,8:30,1030,12:30,1430,1630的温度。 2.已知1g(x1,101]区间11个整数采样点x=1:10:101的函数值g(9,试求gx)的5次 拟合多项式p(x,并分别绘制出lg(x)和px)在1,10川区间的函数曲线。 3.求以下非线性方程组的解: 2x-x =e -+x=e 4.求以下有约束最值: 第8页
《数学建模与数学实验》实验指导书 第8页 (X.^2+1./X.^2)' %显示求解函数与采样点对应的一组解析解 例: 求解常微分方程组初值问题在区间[0,2]中的解。 2 1 2 2 2 (0) 5 5 (0) 6 dy y y dx dy xy x y dx = = = − + − = 1 2 , , 建立一个函数文件 fxy2.m: function f=f(x,y) f(1)=y(2); f(2)=-x.*y(2)+x.^2-5; f=f'; 在 MATLAB 命令窗口,输入命令: [X,Y]=ode45('fxy2',[0,2],[5,6]) 基础实验八:matlab 数值计算 实验目的:掌握用 matlab 进行插值、拟合、方程求解等数值计算的方法。 实验内容: 1. 某气象观测站测得某日 6:00-18:00 之间每隔 2 小时的温度如下: 时间 6 8 10 12 14 16 18 温度 18 20 22 25 30 28 24 试用三次样条插值求出该日 6:30,8:30,10:30,12:30,14:30,16:30 的温度。 2. 已知 lg(x)在[1,101]区间 11 个整数采样点 x=1:10:101 的函数值 lg(x),试求 lg(x)的 5 次 拟合多项式 p(x),并分别绘制出 lg(x)和 p(x)在[1,101]区间的函数曲线。 3. 求以下非线性方程组的解: 1 2 1 2 1 2 2 x x x x e x x e − − − = − + = 4. 求以下有约束最值:

《数学建模与数学实验》实验指导书 minf(x.y)=x+y [x2+y2≤1 2x-y20 提示: ●一维插值:Y1=interpl(X,Y,X1,method 1.函数根据X、Y的值,计算函数在X1处的值。X、Y是两个等长的已知向量,分 别描述采样点和样本值,X1是一个向量或标量,描述欲插值的点,Y1是一个与 X等长的插值结果。method是插值方法,允许的取值有linear(线性插值)、nearest(最 近插值)、'spline'(三次样条插值)、cubic(三次多项式插值),缺省值是linear。 ·多项式拟合:PS]=polyfit(XYm) 1.函数根据采样点X和采样点函数值Y,产生一个m次多项式P及其在采样点的误 差向量S。 2.其中X、Y是两个等长的向量,P是一个长度为m+1的向量。 ·单变量非线性方程求解:[x.fval]=-fzero(Ex0,tol) [x,fval]=fmincon(fun.x0.A.b.Aeq.beq.Ib,ub.nonlcon) L.fun是一个函数文件functionf=fun(x)。x0是初始值。 2.A,Aeq是一个矩阵;b,beg是一个列向量。Ax<b是不等式约束。 3.b和b是和x一样大小的列向量,规定每个分量的上下界 4.nonlcon是函数文件,有特定格式function [e,ceo=mycon((x),描述非线性约束cx) 和ceq(x). 5.没有整数约束,0-1约束,敏感性分析 基础实验九:求解图论问题 实验目的:把最短路径、最大流、最小生成树、旅行商、关键路径等图论问题转化为数学规 划模型,并用Lingo进行求解 实验内容: 把以下图从v0到v6最短路径问题转化为数学规划模型,并用Ligo进行求解。 第9页
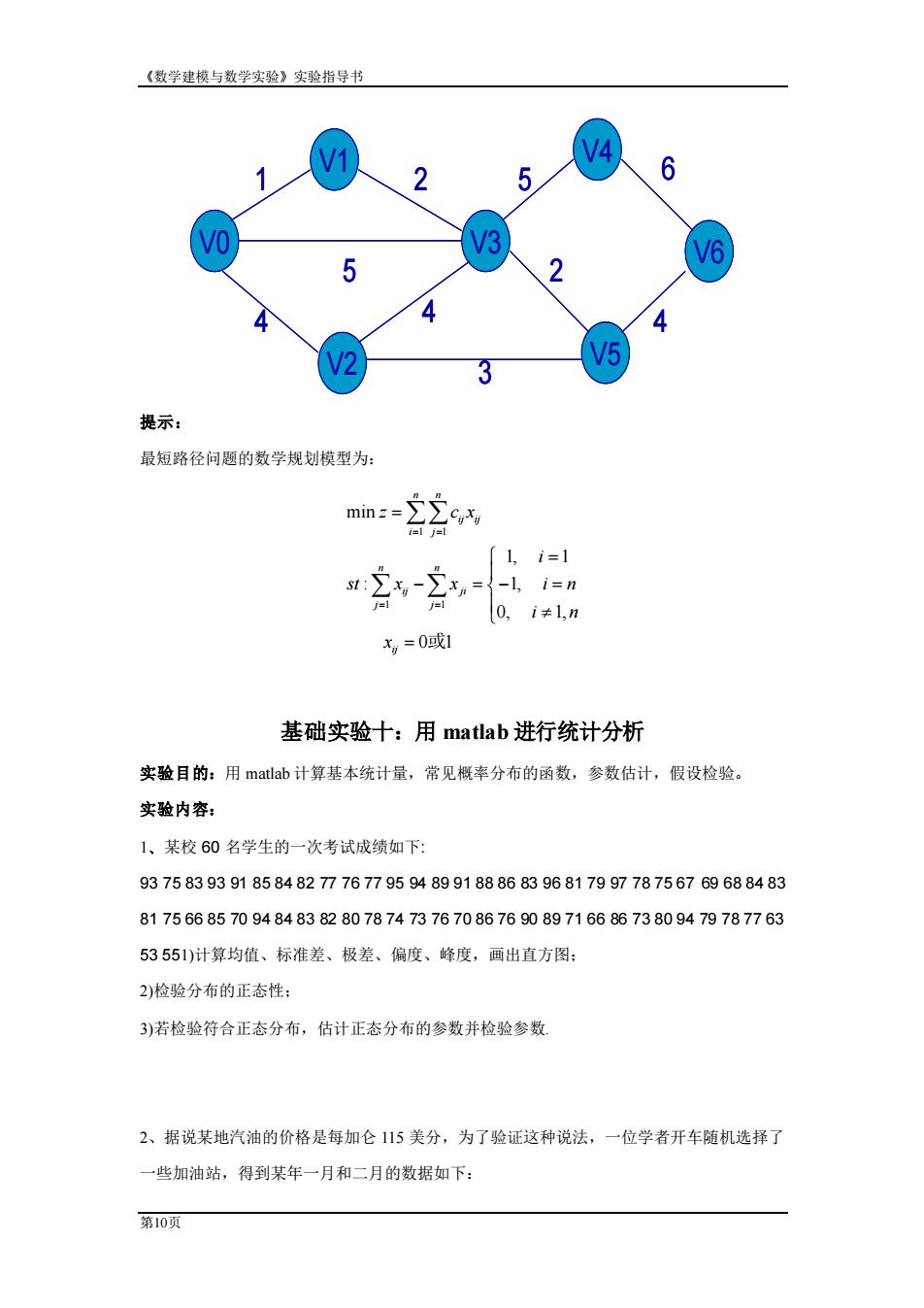
《数学建模与数学实验》实验指导书 第9页 2 2 min ( , ) 1 2 0 f x y x y x y x y = + + − 提示: ⚫ 一维插值:Y1=interp1(X,Y,X1,'method') 1. 函数根据 X、Y 的值,计算函数在 X1 处的值。X、Y 是两个等长的已知向量,分 别描述采样点和样本值,X1 是一个向量或标量,描述欲插值的点,Y1 是一个与 X1等长的插值结果。method是插值方法,允许的取值有'linear'(线性插值)、'nearest'(最 近插值)、'spline'(三次样条插值)、'cubic'(三次多项式插值),缺省值是'linear'。 ⚫ 多项式拟合:[P,S]=polyfit(X,Y,m) 1. 函数根据采样点 X 和采样点函数值 Y,产生一个 m 次多项式 P 及其在采样点的误 差向量 S。 2. 其中 X、Y 是两个等长的向量,P 是一个长度为 m+1 的向量。 ⚫ 单变量非线性方程求解:[x,fval]=fzero(f,x0,tol) ⚫ [x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) 1. fun 是一个函数文件 function f = fun(x)。x0 是初始值。 2. A,Aeq 是一个矩阵;b,beq 是一个列向量。Ax<=b 是不等式约束。 3. lb 和 ub 是和 x 一样大小的列向量,规定每个分量的上下界。 4. nonlcon 是函数文件,有特定格式 function [c,ceq] = mycon(x),描述非线性约束 c(x) 和 ceq(x)。 5. 没有整数约束,0-1 约束,敏感性分析。 基础实验九:求解图论问题 实验目的:把最短路径、最大流、最小生成树、旅行商、关键路径等图论问题转化为数学规 划模型,并用 Lingo 进行求解。 实验内容: 把以下图从 v0 到 v6 最短路径问题转化为数学规划模型,并用 Lingo 进行求解
《数学建模与数学实验》实验指导书 V6 5 4 提示: 最短路径问题的数学规划模型为: m- 「1,i=1 0,i≠l,n ,=0或1 基础实验十:用matlab进行统计分析 实验目的:用matlab计算基本统计量,常见概率分布的函数,参数估计,假设检验 实验内容: 1、某校60名学生的一次考试成绩如下 937583939185848277677959489918886839681799778756769688483 8175668570948483828078747376708676908971668673809479787763 53551)计算均值、标准差、极差、偏度、峰度,画出直方图: 2)检验分布的正态性: 3)若检验符合正态分布,估计正态分布的参数并检验参数 2、据说某地汽油的价格是每加仑115美分,为了验证这种说法,一位学者开车随机选择了 一些加油站,得到某年一月和二月的数据如下: 第10项
《数学建模与数学实验》实验指导书 第10页 V0 V3 V6 V5 V4 V1 V2 1 5 4 4 3 2 4 6 2 5 V0 V3 V6 V5 V4 V1 V2 1 5 4 4 3 2 4 6 2 5 提示: 最短路径问题的数学规划模型为: 1 1 1 1 min 1, 1 : 1, 0, 1, 0 1 n n ij ij i j n n ij ji j j ij z c x i st x x i n i n x = = = = = = − = − = = 或 基础实验十:用 matlab 进行统计分析 实验目的:用 matlab 计算基本统计量,常见概率分布的函数,参数估计,假设检验。 实验内容: 1、某校 60 名学生的一次考试成绩如下: 93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 551)计算均值、标准差、极差、偏度、峰度,画出直方图; 2)检验分布的正态性; 3)若检验符合正态分布,估计正态分布的参数并检验参数. 2、据说某地汽油的价格是每加仑 115 美分,为了验证这种说法,一位学者开车随机选择了 一些加油站,得到某年一月和二月的数据如下: