
向量组的孩恨相关烟 第五节 线性方程组的解的结构 齐次方程组解的性质 基础解系及其求法 三 非齐次方程组解的性质 四、小结思考题 返

一、齐次线性方程组解的性质 1.解向量的概念 设有齐次线性方程组 011S1+a12x2+.+41nXn=0 21x1+22x2+.+02mxn=0 (1) m1x1+m2X2+.+AmXn=0 若记 上页 返回
1.解向量的概念 设有齐次线性方程组 + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x 若记 (1) 一、齐次线性方程组解的性质

411 12 主王二二二二二二二二王王 a21 42 A- x= . : Aml am2 则上述方程组(1)可写成向量方程 Ax=0. 若x1=51,x2=521,xn=51为方程Ax=0的 解,则 上页 下
, a a a a a a a a a A m m mn n n = 1 2 2 1 2 2 2 1 1 1 2 1 = xn x x x 2 1 则上述方程组(1)可写成向量方程 Ax = 0. 1 1 1 2 2 1 xn n1 若 x = , x = ,, = 为方程 Ax = 0 的 解,则

x=51= 称为方程组(1)的解向量,它也就是向量方程 (2)的解. 上页 区回
= = 1 21 11 1 n x 称为方程组(1) 的解向量,它也就是向量方程 (2)的解.

2. 齐次线性方程组解的性质 (1)若x=5,x=52为Ax=0的解,则 x=51+52 也是Ax=0的解 证明:A51=0,A52=0 ∴.A(5+52)=A5+A52=0 故x=5+52也是Ax=0的解 页
2.齐次线性方程组解的性质 (1)若 x = 1 ,x = 2 为 Ax = 0 的解,则 x = 1 + 2 也是 Ax = 0 的解. 证明 A( 1 + 2 ) = A 1 + A 2 = 0 A 1 = 0, A 2 = 0 故 x 也是Ax 0的解. = 1 + 2 =

(2)若x=51为Ax=0的解,k为实数,则 x=k51也是Ax=0的解. 证明A(k51)=kA(5)=k0=0. 证毕. 由以上两个性质可知,方程组的全体解向量 所组成的集合,对于加法和数乘运算是封闭的, 因此构成一个向量空间,称此向量空间为齐次线 性方程组A化=0的解空间. 回
(2)若 为 的解, 为实数,则 也是 的解. x = 1 Ax = 0 k x = k 1 Ax = 0 证明 A(k ) kA( ) k0 0. 1 = 1 = = 由以上两个性质可知,方程组的全体解向量 所组成的集合,对于加法和数乘运算是封闭的, 因此构成一个向量空间,称此向量空间为齐次线 性方程组 Ax = 0 的解空间. 证毕

二、基础解系及其求法 1.基础解系的定义 1,门2,.,7,称为齐次线性方程组4x=0的基础 解系,如果 (I)n1,2,7,是Ax=0的一组线性无关的解 (2)Ax-0的任一解都可由n1,72,7线性表 出
解 系 如 果 称为齐次线性方程组 的基础 , 1 ,2 ,,t Ax = 0 (1) , , , 0 ; 1 2 t是Ax = 的一组线性无关的解 . (2) 0 , , , 1 2 出 Ax = 的任一解都可由 t线性表 1.基础解系的定义 二、基础解系及其求法

如果71,72,.,7,为齐次线性方程组Ax=0 的一组基础解系,那么,Ax=0的通解可表示为 x=kn+k22+.+kn 其中k1,k2,kn,是任意常数 上页 这回
的一组基础解系 那么 的通解可表示为 如果 为齐次线性方程组 0 = = Ax t Ax , , 1 ,2 ,, 0 x = k11 + k22 ++ ktt , , , . 其中k1 k2 kn−r是任意常数

2.线性方程组基础解系的求法 设齐次线性方程组的系数矩阵为A,并不妨 设A的前r个列向量线性无关.于是A可化为 0b1 1 A~ 0 brn-r 0 0 0
2.线性方程组基础解系的求法 − − 0 0 0 0 0 1 1 0 ~ 1 , 1 1 1, r r n r n r b b b b A 设齐次线性方程组的系数矩阵为 ,并不妨 设 的前 r 个列向量线性无关.于是 可化为 A A A
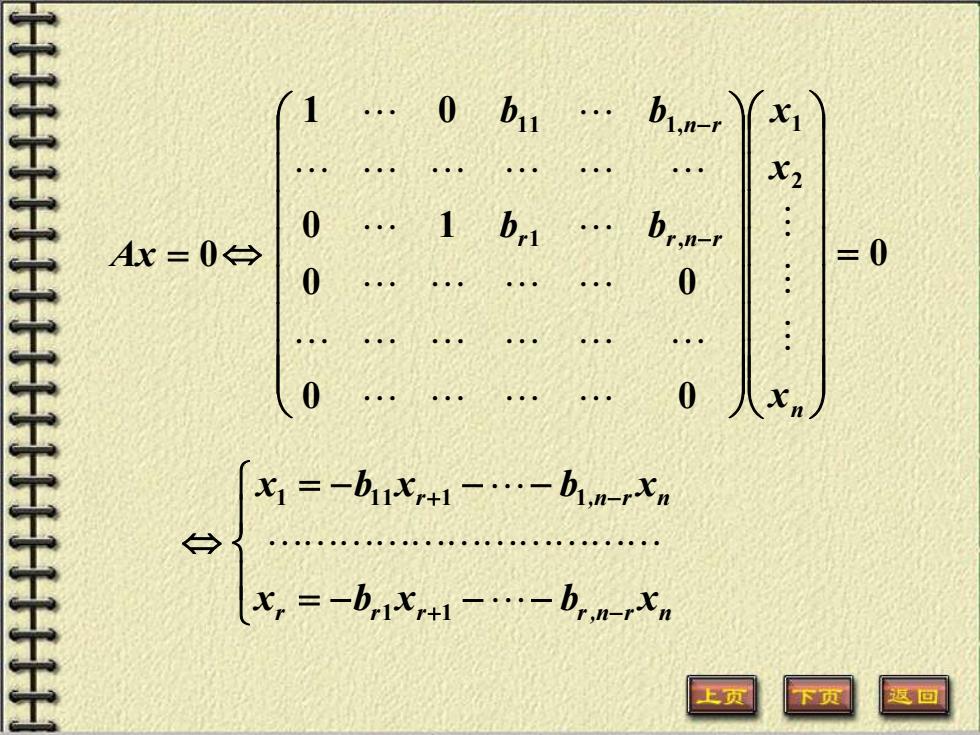
1 . 0b11 b1,n- 0 1 b Ax=0→ =0 0 0 0 X1=-bu-binXn → x,=-b1x+1-b,m-,x 这回
0 0 0 0 0 0 1 1 0 2 1 1 , 1 1 1, = − − n r r n r n r x x x b b b b = − − − = − − − + − + − r r r r,n r n r ,n r n x b x b x x b x b x 1 1 1 1 1 1 1 Ax = 0