
相似矩连及二次型 第三节 相似矩阵 一、相以矩阵与相以变换的概念 相似矩阵与相似变换的性质 三、 利用相似变换将方阵对角化 四、小结思考题 助

相似矩阵与相似变换的概念 定义1设A,B都是n阶矩阵,若有可逆矩阵P,使 PAP=B, 则称B是A的相似矩阵或说矩阵A与B相似对A进 行运算P-AP称为对A进行相似变换可逆矩阵P 称为把A变成B的相似变换矩阵
一、相似矩阵与相似变换的概念 . , , . , 1 , , , 1 1 称为把 变 成 的相似变换矩阵 行运算 称为对 进行相似变换可逆矩阵 则 称 是 的相似矩阵 或说矩阵 与 相 似 对 进 定 义 设 都 是 阶矩阵 若有可逆矩阵 使 A B P AP A P B A A B A P AP B A B n P − − =

二、相似矩阵与相似变换的性质 1.等价关系 (I)反身性A与A本身相似 (2)对称性若A与B相似,则B与A相似. (3)传递性 若A与B相似,B与C相似, 则A与C相似. 2.p1(A,42)P=-(PA,PP-A,P) 3.若A与B相似,则Am与Bm相似(m为正整数)
1. 等价关系 2. ( ) ( )( ). 2 1 1 1 1 2 1 P A A P P A P P A P − − − = 3.若A与B相似,则A 与B 相似(m为正整数). m m 二、相似矩阵与相似变换的性质 A与A本身相似. 若A与B相似,则B与A相似. . , , 则 与 相似 若 与 相似 与 相似 A C A B B C (1)反身性 (2)对称性 (3)传递性

4.P-k 4 +k24)P=k P-A P+k2P-A2 P 其中k1,k2是任意常数. 定理1若n阶矩阵A与B相似,则A与B的特征多项 式相同,从而A与B的特征值亦相同 证明A与B相似 →可逆阵P,使得P-AP=B ∴B-E=P-AP-P(2E)P =P-(A-E)P P-A-AE P =A-2E. 上页 湖回
证明 A与B相似 B E P AP P (E)P −1 −1 − = − = P (A − E)P −1 = P A− E P −1 = A − E . P (k A k A )P k P A P k P A2P 1 1 2 1 1 1 2 2 1 1 4. − − − + = + , . 其中k1 k2是任意常数 P P AP = B −1 可逆阵 ,使得 , . 1 , 式相同 从 而 与 的特征值亦相同 定 理 若 阶矩阵 与 相 似 则 与 的特征多项 A B n A B A B

推论 若n阶方阵A与对角阵 相似,则2,22,2n即是A的n个特征值 上页 返回
推论 若 n 阶方阵A与对角阵 = n 2 1 , , , , . 相似 则1 2 n即是A的n个特征值

利用对角矩阵计算矩阵多项式 若A=PBP,则 k个 A-PBP-PBP-1.PBP-PBPD PBP A的多项式 (A)=aoA"+aA"++an-14+anE =aoPB"p'+a1PB-P-+. +an-PBP+an PE P- P(ao B"+aiB"++anB+an E)P =Pp(B)P-1
利用对角矩阵计算矩阵多项式 , 1 A PB P − 若 = a PB P a PE P a P B P a P B P n n n n 1 1 1 1 1 1 1 0 − − − − − − + + = + + A = k A的多项式 A a A a A an A anE n n = + + + − + − 1 1 0 1 ( ) ( ) . 1 P B P− = . 1 P B Pk − = 则 P a B a B an B anE P n n 1 1 1 0 1 ( ) − − − = + ++ + PB P − 1 PBP−1 PBP−1 PBP−1 k个
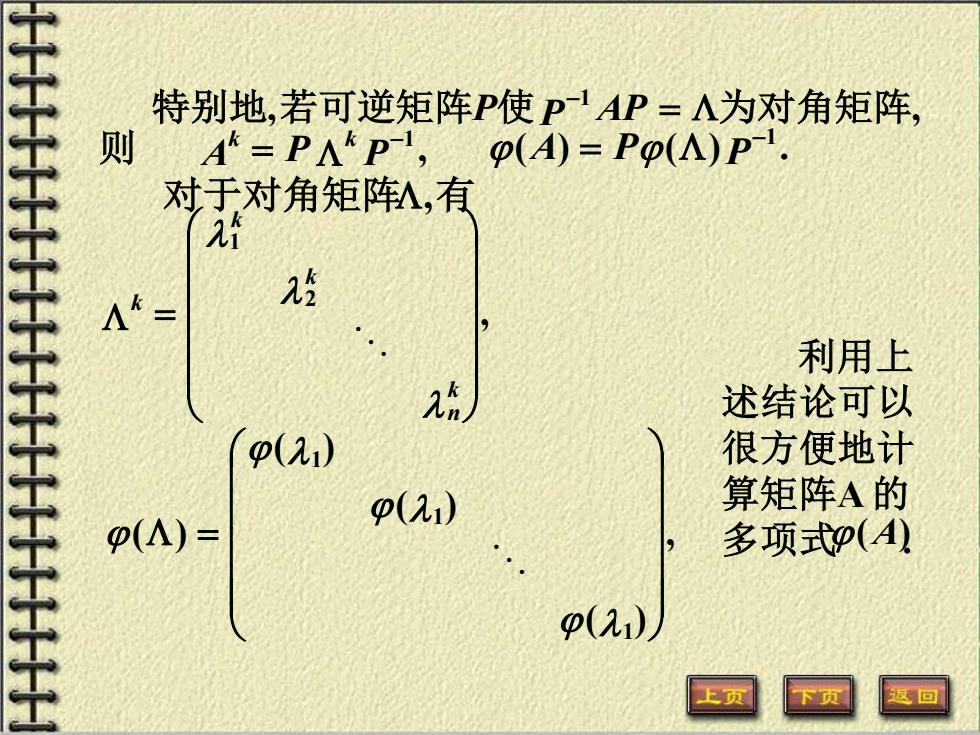
特别地,若可逆矩阵P使P1AP=人为对角矩阵, 则 A=PA*P-,(A)=Po(A)P. 对于对角矩阵私,有 2 k= 始 利用上 述结论可以 p(2) 很方便地计 Q(A)- p(2) 算矩阵A的 多项式P(A) p(21) 回
, , 特别地 若可逆矩阵P使P −1 AP = 为对角矩阵 , 1 A P P k k − 则 = ( ) ( ) . 1 A P P − = 对于对角矩阵,有 , 2 1 = k n k k k , ( ) ( ) ( ) ( ) 1 1 1 = 利用上 述结论可以 很方便地计 算矩阵A 的 多项式 . (A)

定理 设f(2)是矩阵A的特征多项式则f(A)=O, 证明只证明A与对角矩阵相似的情形 若A与对角矩阵相似,则有可逆矩阵P,使 P AP=A=diag(,), 其中2;为A的特征值f(2)=0.由A=PAP,有 f(2) f(A)=Pf(A)P=P =P0P-1=O
定理 设f ()是矩阵A的特征多项式,则f (A) = O. 证明 只证明A与对角矩阵相似的情形. 若A与对角矩阵相似,则有可逆矩阵P,使 ( , , ), 1 1 P AP = = diag n − , ( ) = 0. i i 其中 为A的特征值 f 由A = P P −1 ,有 f (A) . 1 = PO P = O − Pf P 1 ( ) − = P f f P n 1 1 ( ) ( ) − =

三、利用相似变换将方阵对角化 对n阶方阵A,若可找到可逆矩阵P,使 P-1AP=∧为对角阵,这就称为把方阵A对角化. 定理2n阶矩阵A与对角矩阵相以即A能对角化 王王王王王王王王王王 的充分必要条件是4有个线性无关的特征向量 证明 假设存在可逆阵靶,使PAP=A为对角阵 把P用其列向量表示为P=(p1,P2,Pn):
, . , , 1 为对角阵 这就称为把方阵 对角化 对 阶方阵 若可找到可逆矩阵 使 P AP A n A P = − 证明 , , 假设存在可逆阵P 使P −1AP = 为对角阵 ( , , , ) . 把 P 用其列向量表示为P = p1 p2 pn 三、利用相似变换将方阵对角化 . 2 ( ) 的充分必要条件是 有 个线性无关的特征向量 定 理 阶矩阵 与对角矩阵相似即 能对角化 A n n A A

由P1AP=A,得AP=PA, 即4A(p1,P2,Pn)=(p1,P2,pn) 22 =(21P1,2P2,nDn) .A(BB2,P)=(AB,Ap2Ap) =(1P1,p2,pn) 于是有 4p:=p;((i=1,2,n 上页
( ) ( ) = n n n A p p p p p p 2 1 1 2 1 2 即 , , , , , , ( , , , ). = 1 p1 2 p2 n pn ( ) ( ) A p p pn Ap Ap Apn , , , , , , 1 2 = 1 2 Ap p (i 1,2, ,n). 于是有 i = i i = ( ) p p pn , , , = 1 1 2 , , 1 = = − 由P AP 得AP P