《线性代数》课程PPT教学课件（同济第五版）第2章 矩阵及其运算 2.2 矩阵的运算

矩库及其运氧 第二节 矩阵的运算 矩阵的加法 数与矩阵相乘 三 矩阵与矩阵相乘 四、矩阵的其它运算 五、小结思考题 返

一、矩阵的加法 1、定义 设有两个m×n矩阵A=(a,)B=(b,)那末矩阵 A与B的和记作A+B,规定为 au+bu a2+b2 21+b21 a22+b2 .2n+b2n 4+B- 上页 返回

１、定义               + + + + + + + + + + = m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 一、矩阵的加法 设有两个 矩阵 那末矩阵 与 的和记作 ，规定为 mn A (a ), B (b ), = ij = ij A B A+ B

说明只有当两个矩阵是同型矩阵时，才能进 行加法运算. 12 3 -5 18 9 例如 1 -9 0 + 6 5 4 3 6 8 3 21 12+1 3+8 -5+9 13 11 4 1+6 -9+5 0+4 7 -4 4 3+3 6+2 8+1 6 8 上页

说明 只有当两个矩阵是同型矩阵时，才能进 行加法运算. 例如           +           − − 3 2 1 6 5 4 1 8 9 3 6 8 1 9 0 12 3 5           + + + + − + + + + − + = 3 3 6 2 8 1 1 6 9 5 0 4 12 1 3 8 5 9 . 6 8 9 7 4 4 13 11 4           = −

2、 矩阵加法的运算规律 (1)A+B=B+4; (2)(A+B)+C=A+(B+C) -a11 -a12 (3)-A= -a21 -a2 =(a力 -aml am 称为矩阵A的负矩阵， A+A=0, (4)A-B=A+(-B) 上页 区回

2、 矩阵加法的运算规律 (1) A+ B = B + A; (2)(A+ B)+ C = A+ (B + C). ( ) 11 12 1 21 22 2 1 1 3 n n m m mn a a a a a a A a a a   − − −   − − −   − =       − − − A A + − = ( ) 0, ( ), = − aij 称为矩阵A的负矩阵. (4 . ) A B A B − = + −( )

二、数与矩阵相乘 1、定义 数2与矩阵4的乘积记作2A或A几，规定为 211 212 2A=A几= 221 222 22n . . Aam Aam . Mmn

1、定义 . 1 1 2 1 2 2 2 1 1 1 2 1               = = m m mn n n a a a a a a a a a A A                   二、数与矩阵相乘 数与矩阵A的乘积记作A或A,规定为

2、数乘矩阵的运算规律 (设A、B为m×n矩阵，2，u为数) (1)(U4)A=2(4片 (2)(亿+μ)A=M+4; (3)2(A+B)=A+2B. 矩阵相加与数乘矩阵合起来，统称为矩阵的线 性运算. 回

(1)()A = (A); (2)( + )A = A+ A; (3) (A+ B) = A+ B. 2、数乘矩阵的运算规律 矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算. （设 A、B 为 mn 矩阵，  , 为数）

三、矩阵与矩阵相乘 1、定义 设A=(a,)是一个m×s矩阵，B=(b,)是一个 S×n矩阵，那末规定矩阵A与矩阵B的乘积 是一个m×n矩阵C-(cu),其中 Cy=anbj+anbaj+.+aby =Eaaby (i=1,2,.mj=1,2,.,n), 并把此乘积记作C=AB

１、定义 = + + + =  = s k ij ai b j ai b j ai sbsj ai k bkj c 1 1 1 2 2  (i = 1,2, m; j = 1,2,  ,n), 并把此乘积记作 C = AB. 三、矩阵与矩阵相乘 设 是一个 矩阵， 是一个 矩阵，那末规定矩阵 与矩阵 的乘积 是一个 矩阵 ，其中 ( ) A = aij m s ( ) B = bij sn mn ( )ij C = c A B

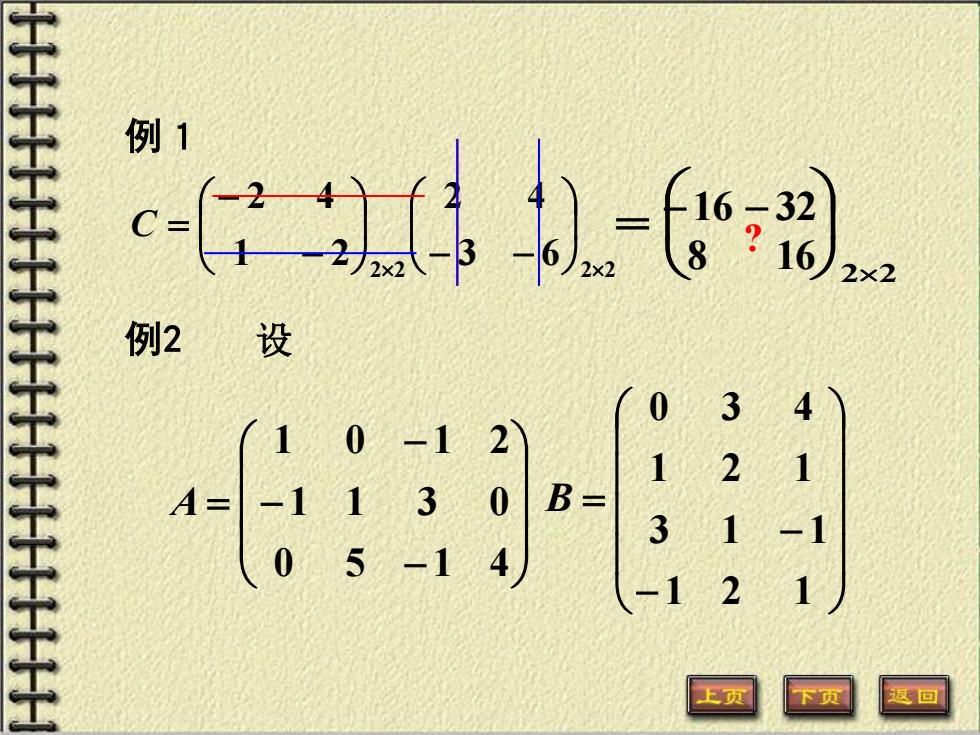
例1 2×2 例2 设 3 (1 0 -1 2 2 A= -1 1 3 0 B- 41 3 1 、05 -1 4 -1 -1 2 上页 区回

例１ 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = −16 − 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ?

解 A=agA4’B=bg3 .C=(c) 故 -5 6 102 -6 -217 10

故   − −   − − − = = 1 2 1 3 1 1 1 2 1 0 3 4 0 5 1 4 1 1 3 0 1 0 1 2 C AB .  = 解 ( ) , 34  A = aij ( )4  3 , B = bij ( ) . 33  = ij C c − 5 6 7 10 2 − 6 − 2 17 10

注意只有当第一个矩阵的列数等于第二个矩阵 的行数时，两个矩阵才能相乘. 2 例如 不存在 tnaa-mn 上页 回

注意 只有当第一个矩阵的列数等于第二个矩阵 的行数时，两个矩阵才能相乘.                 6 0 1 1 6 8 5 8 9 3 2 1 1 2 3 例如 ( )           1 2 3 1 2 3 = (1 3 + 2 2 + 31) = (10). 不存在