
Preliminaries A tree can be defined in several ways.One natural way to define a tree is recursively. A tree is a collection of nodes.The collection can be empty;otherwise,a tree consists of a distinguished node r,called the root and zero or more nonempty (sub)trees 71,72....,7k each of whose roots are connected by a directed edge from / The root of each subtree is said to be a child of, and ris the parent of each subtree root. root 方 万五 万 Ta Tio
Preliminaries ◼ A tree can be defined in several ways. One natural way to define a tree is recursively. ◼ A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty (sub)trees T1 , T2 , …, Tk , each of whose roots are connected by a directed edge from r. ◼ The root of each subtree is said to be a child of r, and r is the parent of each subtree root. root T1 T2 T3 T4 … T10
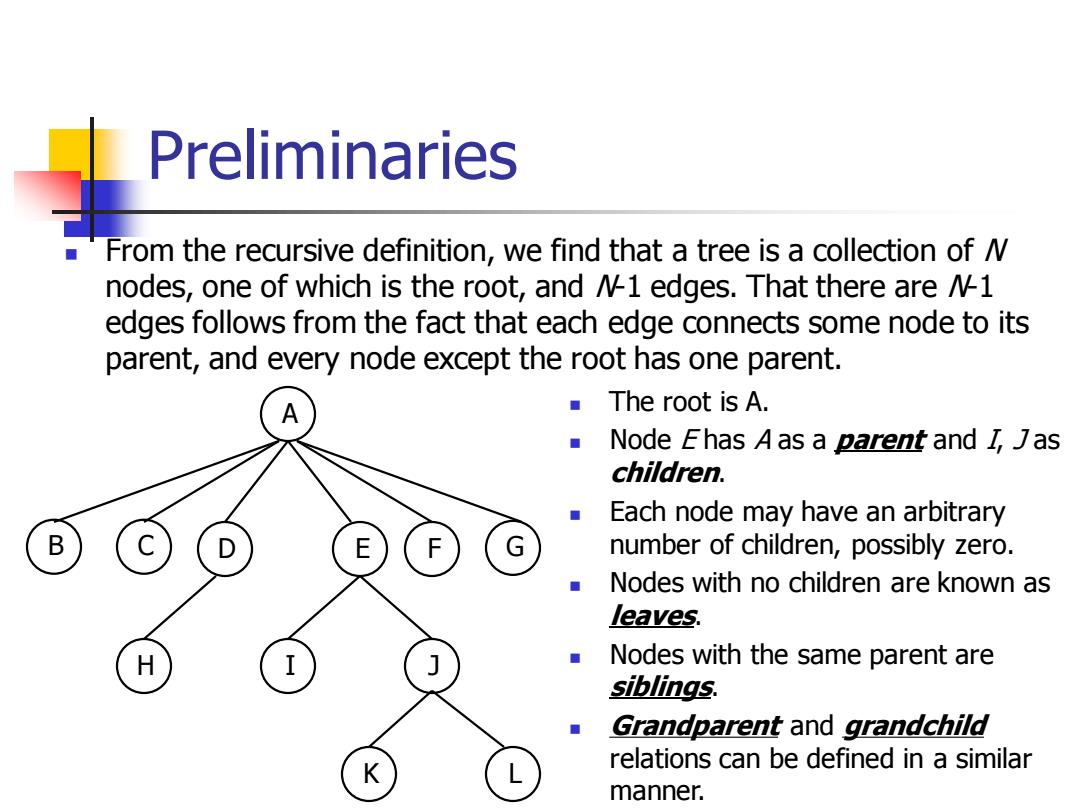
Preliminaries From the recursive definition,we find that a tree is a collection of nodes,one of which is the root,and /1 edges.That there are /1 edges follows from the fact that each edge connects some node to its parent,and every node except the root has one parent. A The root is A. Node Fhas A as a parent and I,Jas children. Each node may have an arbitrary B E number of children,possibly zero. Nodes with no children are known as leaves. H I J Nodes with the same parent are siblings. Grandparent and grandchild K relations can be defined in a similar manner
Preliminaries ◼ From the recursive definition, we find that a tree is a collection of N nodes, one of which is the root, and N-1 edges. That there are N-1 edges follows from the fact that each edge connects some node to its parent, and every node except the root has one parent. A B C D E F G H I J K L ◼ The root is A. ◼ Node E has A as a parent and I, J as children. ◼ Each node may have an arbitrary number of children, possibly zero. ◼ Nodes with no children are known as leaves. ◼ Nodes with the same parent are siblings. ◼ Grandparent and grandchild relations can be defined in a similar manner

Preliminaries A path from node n to n is defined as a sequence of nodes m,n,n...,nk such that n is the parent of n for 1≤Kk The length of this path is the number of edges on the path,namely k1.There is a path of length zero from every node to itself.Notice that in a tree there is exactly one path from the root to each node
Preliminaries ◼ A path from node n1 to nk is defined as a sequence of nodes n1 , n2 , n3…, nk such that ni is the parent of ni+1 for 1i<k. ◼ The length of this path is the number of edges on the path, namely k-1. There is a path of length zero from every node to itself. Notice that in a tree there is exactly one path from the root to each node

Preliminaries For any node n the depth of n;is the length of the unique path from the root to /,Thus,the root is at depth 0.The height of n,is the length of the longest path from n,to a leaf.Thus all leaves are at height 0.The height of a tree is equal to the height of the root.The depth of a tree is equal to the depth of the deepest leaf;this is always equal to the height of the tree. If there is a path from m to m,then m is an ancestor of m and m is a descendant of m.If mtm,then m is a proper ancestor of m and m is a proper descendant of m
Preliminaries ◼ For any node ni , the depth of ni is the length of the unique path from the root to ni . Thus, the root is at depth 0. The height of ni is the length of the longest path from ni to a leaf. Thus all leaves are at height 0. The height of a tree is equal to the height of the root. The depth of a tree is equal to the depth of the deepest leaf; this is always equal to the height of the tree. ◼ If there is a path from n1 to n2 , then n1 is an ancestor of n2 and n2 is a descendant of n1 . If n1n2 , then n1 is a proper ancestor of n2 and n2 is a proper descendant of n1
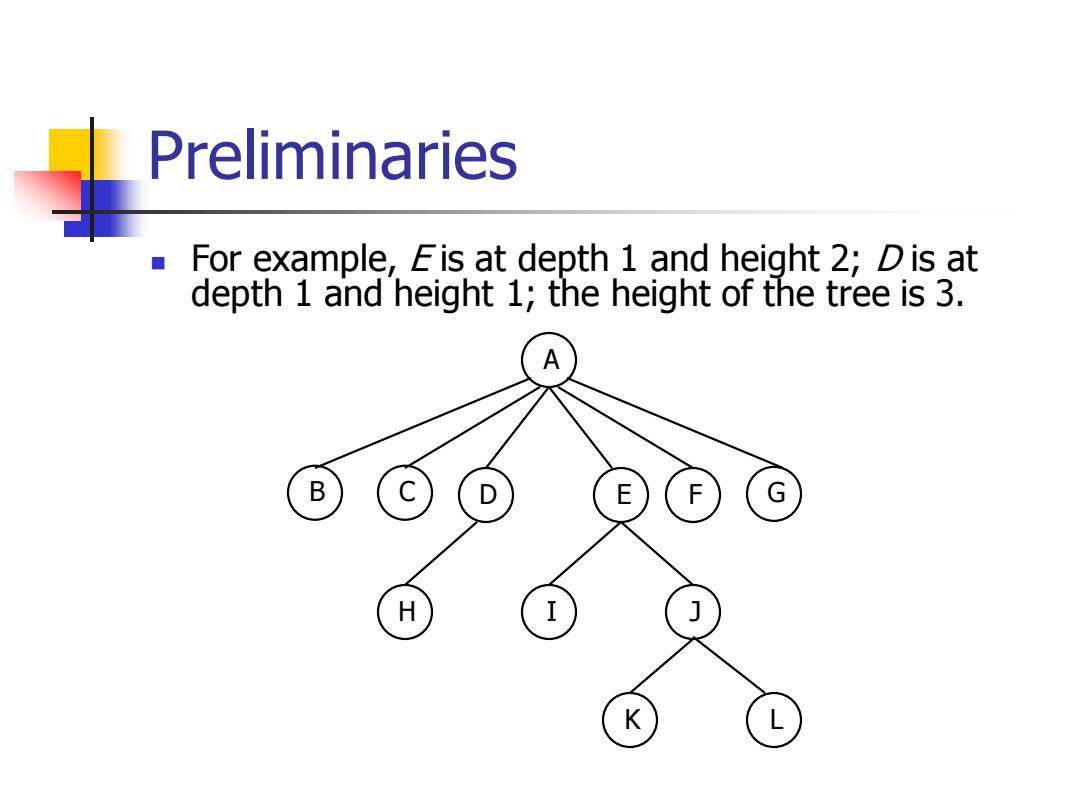
Preliminaries For example,Eis at depth 1 and height 2;Dis at depth 1 and height 1;the height of the tree is 3. A B D E G H I J K
Preliminaries ◼ For example, E is at depth 1 and height 2; D is at depth 1 and height 1; the height of the tree is 3. A B C D E F G H I J K L

Implementation of Trees One way to implement a tree would be to have in each node,besides its data,a pointer to each child of the node. However,since the number of children per node can vary so greatly and is not known in advance,it might be infeasible to make the children direct links in the data structure,because there would be too much wasted space. The solution is simple:Keep the children of each node in a linked list of tree nodes
Implementation of Trees ◼ One way to implement a tree would be to have in each node, besides its data, a pointer to each child of the node. ◼ However, since the number of children per node can vary so greatly and is not known in advance, it might be infeasible to make the children direct links in the data structure, because there would be too much wasted space. ◼ The solution is simple: Keep the children of each node in a linked list of tree nodes

Implementation of Trees struct TreeNode { char Element; TreeNode*FirstChild; TreeNode*NextSibling; )
Implementation of Trees struct TreeNode { char Element; TreeNode* FirstChild; TreeNode* NextSibling; }
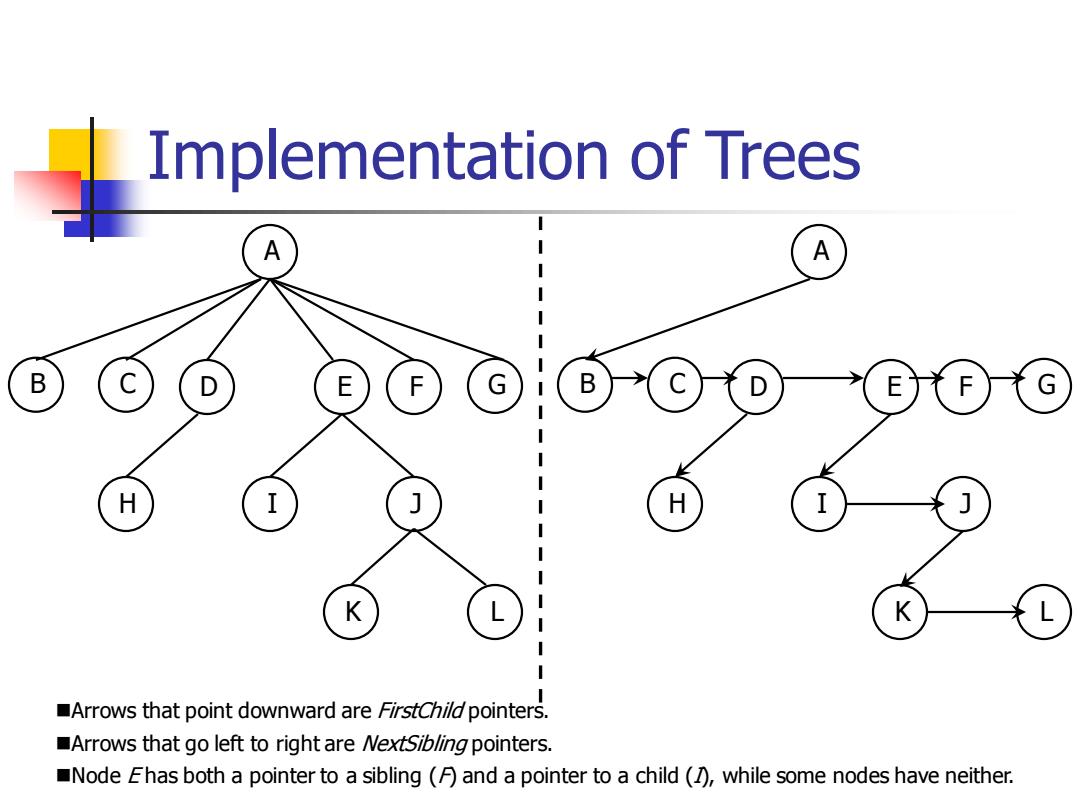
Implementation of Trees A I A B C D E F H I H I J K K I Arrows that point downward are FirstChild pointers. Arrows that go left to right are NextSib/ing pointers. Node Ehas both a pointer to a sibling (A)and a pointer to a child (while some nodes have neither
Implementation of Trees A B C D E F G H I J K L A B C D E F G H I J K L ◼Arrows that point downward are FirstChild pointers. ◼Arrows that go left to right are NextSibling pointers. ◼Node E has both a pointer to a sibling (F) and a pointer to a child (I), while some nodes have neither

Implementation of Trees Example:Please give the first child/next sibling representation of the following tree. A B C D E F G H I J K
Implementation of Trees A B C D E H F G I J ◼ Example: Please give the first child/next sibling representation of the following tree. K L

Application of Trees There are many applications for trees.One of the popular uses is the directory structure in many common operating systems. /usr* mark* alex* bi训* course* junk.c prog1.r prog2.r The root of this directory is /usr. ■ The asterisk next to the name indicates that /usr is itself a directory
mark* alex* bill* course* junk.c prog1.r prog2.r /usr* Application of Trees ◼ There are many applications for trees. One of the popular uses is the directory structure in many common operating systems. ◼ The root of this directory is /usr. ◼ The asterisk next to the name indicates that /usr is itself a directory