
The Disjoint Set ADT In this part,we describe an efficient data structure to solve the eguivalence problem. ■ Relations:A relation R is defined on a set Sif for every pair of elements (a,b),a,bes,a Rb is either true or false.If a R b is true,then we say that a is related to 6
The Disjoint Set ADT ◼ In this part, we describe an efficient data structure to solve the equivalence problem. ◼ Relations: A relation R is defined on a set S if for every pair of elements (a, b), a, bS, a R b is either true or false. If a R b is true, then we say that a is related to b

The Disjoint Set ADT Equivalence Relations:An equivalence relation is a relation R that satisfies three properties: Reflexive:a R a,for all aeS; Symmetric:a R b if and only if b R a; Transitive:a R b and b R cimplies that a R c The relationship is not an equivalence relationship. Two cities are related if they are in the same country.This relation is an equivalence relation if all the roads are two-way
The Disjoint Set ADT ◼ Equivalence Relations: An equivalence relation is a relation R that satisfies three properties: ✓ Reflexive: a R a, for all aS; ✓ Symmetric: a R b if and only if b R a; ✓ Transitive: a R b and b R c implies that a R c; ◼ The relationship is not an equivalence relationship. ◼ Two cities are related if they are in the same country. This relation is an equivalence relation if all the roads are two-way

The Disjoint Set ADT Given an equivalence relation ~the natural problem is to decide,for any a and b,if ab. The equivalence class of an element aeSis the subset of S that contains all the elements that are related to a. Notice that the equivalence classes from a partition of S:Every member of S appears in exactly one equivalence class
The Disjoint Set ADT ◼ Given an equivalence relation ~, the natural problem is to decide, for any a and b, if a~b. ◼ The equivalence class of an element aS is the subset of S that contains all the elements that are related to a. ◼ Notice that the equivalence classes from a partition of S: Every member of S appears in exactly one equivalence class

The Disjoint Set ADT To decide if ab,we need only to check whether a and b are in the same equivalence class.This provides our strategy to solve the equivalence problem. The input is initially a collection of Nsets,each with one element.Each set has a different element. There are two permissible operations
The Disjoint Set ADT ◼ To decide if a~b, we need only to check whether a and b are in the same equivalence class. This provides our strategy to solve the equivalence problem. ◼ The input is initially a collection of N sets, each with one element. Each set has a different element. ◼ There are two permissible operations

The Disjoint Set ADT The first is Find,which returns the name of the set (that is,the equivalence class)containing a given element. The second operation adds relations.If we want to add the relation a~b,then we first see if a and b are already related.This is done by performing Findson both a and b and checking whether they are in the same equivalence class. If they are not,then we apply Union.This operation merges the two equivalence classes containing a and b into a new equivalence class
The Disjoint Set ADT ◼ The first is Find, which returns the name of the set (that is, the equivalence class) containing a given element. ◼ The second operation adds relations. If we want to add the relation a~b, then ✓ we first see if a and b are already related. This is done by performing Finds on both a and b and checking whether they are in the same equivalence class. ✓ If they are not, then we apply Union. This operation merges the two equivalence classes containing a and b into a new equivalence class

The Disjoint Set ADT Notice that we do not perform any operations comparing the relative values of elements,but merely require knowledge of their location. For this reason,we can assume that all the elements have been numbered sequentially from 1 to M.Thus,initially we have s=for /1 through M
The Disjoint Set ADT ◼ Notice that we do not perform any operations comparing the relative values of elements, but merely require knowledge of their location. ◼ For this reason, we can assume that all the elements have been numbered sequentially from 1 to N. Thus, initially we have Si={i} for i=1 through N

The Disjoint Set ADT Our second observation is that the name of the set returned by Find is actually fairly arbitrary.All that really matters is that Find(a)=Find(b)if and only if a and b are in the same set. Thus,one idea might be to use a tree to represent each set,since each element in a tree has the same root.Therefore,the root can be used to name the set
The Disjoint Set ADT ◼ Our second observation is that the name of the set returned by Find is actually fairly arbitrary. All that really matters is that Find(a)=Find(b) if and only if a and b are in the same set. ◼ Thus, one idea might be to use a tree to represent each set, since each element in a tree has the same root. Therefore, the root can be used to name the set

The Disjoint Set ADT We will represent each set by a tree.Initially,each set contains one element. ■ The representation of the trees is easy,because the only information we will need is a parent pointer. Since only the name of the parent is required,we can assume that this tree is stored implicitly in an array: each entry Ai]in the array represents the parent of element i.If /is a root,then Ail=0
The Disjoint Set ADT ◼ We will represent each set by a tree. Initially, each set contains one element. ◼ The representation of the trees is easy, because the only information we will need is a parent pointer. ◼ Since only the name of the parent is required, we can assume that this tree is stored implicitly in an array: each entry P[i] in the array represents the parent of element i. If i is a root, then P[i]=0
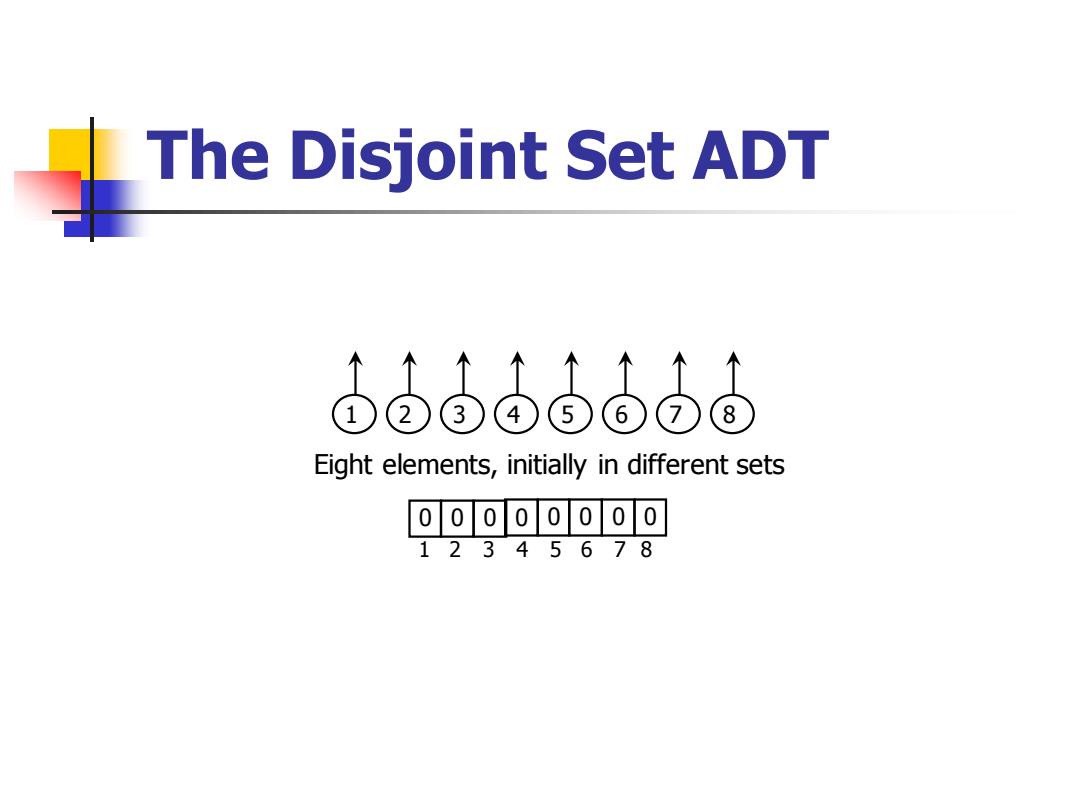
The Disjoint Set ADT ooo56086 Eight elements,initially in different sets 00000000 12345678
The Disjoint Set ADT 1 2 3 4 5 6 7 8 Eight elements, initially in different sets 0 0 0 0 0 0 0 1 2 3 4 5 6 7 0 8
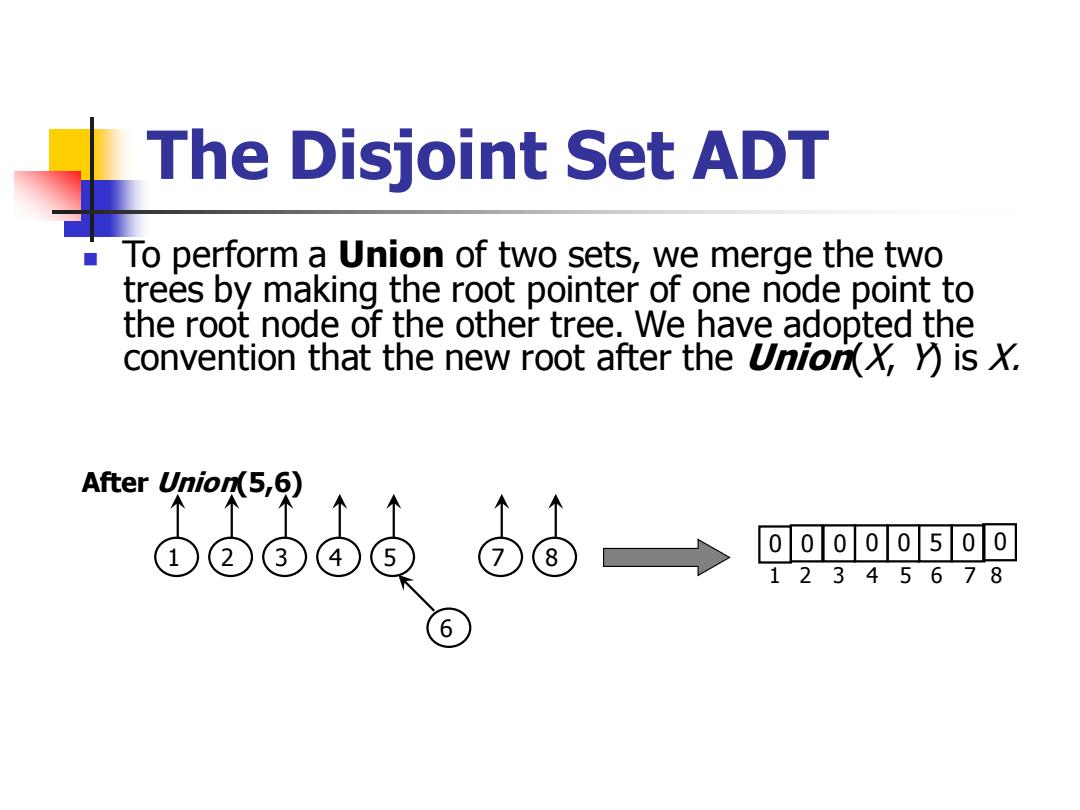
The Disjoint Set ADT To perform a Union of two sets,we merge the two trees by making the root pointer of one node point to the root node of the other tree.We have adopted the convention that the new root after the Union(X,y)is X. After Union(5,6) (4 00o00500 12345678
The Disjoint Set ADT ◼ To perform a Union of two sets, we merge the two trees by making the root pointer of one node point to the root node of the other tree. We have adopted the convention that the new root after the Union(X, Y) is X. 1 2 3 4 5 6 7 8 After Union(5,6) 0 0 0 0 5 0 0 1 2 3 4 5 6 7 0 8