
General Idea Example:Suppose there are a sequence of jobs are sent to a printer.Although jobs sent to a printer are generally placed on a queue,this might not always be the best thing to do. For instance,if,when the printer becomes available, there are several 1-page jobs and one 100-page job, it might be reasonable to make the long job go last, even if it is not the last job submitted. This particular application seems to require a special kind of queue,known as a priority queue
General Idea ◼ Example: Suppose there are a sequence of jobs are sent to a printer. Although jobs sent to a printer are generally placed on a queue, this might not always be the best thing to do. ◼ For instance, if, when the printer becomes available, there are several 1-page jobs and one 100-page job, it might be reasonable to make the long job go last, even if it is not the last job submitted. ◼ This particular application seems to require a special kind of queue, known as a priority queue

Model A priority gueue is a data structure that allows at least the following two operations: (1)Insert:is the equivalent of Engueue (2)DeleteMin:finds,returns,and removes the minimum element in the priority queue. DeleteMin(H) Insert(H) Priority Queue H
Model ◼ A priority queue is a data structure that allows at least the following two operations: ◼ (1) Insert: is the equivalent of Enqueue ◼ (2) DeleteMin: finds, returns, and removes the minimum element in the priority queue. Priority Queue H DeleteMin(H) Insert(H)

Simple Implementations There are several obvious ways to implement a priority queue.We could use a simple linked list performing insertions at the front and traversing the list to delete the minimum. Alternatively,we could insist that the list be kept always sorted. Another way of implementing priority queues would be to use a binary search tree.Recall that the only element we ever delete is the minimum.Repeatedly removing a node that is in the left subtree would seem to hurt the balance of the tree by making the right subtree heavy
Simple Implementations ◼ There are several obvious ways to implement a priority queue. We could use a simple linked list, performing insertions at the front and traversing the list to delete the minimum. ◼ Alternatively, we could insist that the list be kept always sorted. ◼ Another way of implementing priority queues would be to use a binary search tree. Recall that the only element we ever delete is the minimum. Repeatedly removing a node that is in the left subtree would seem to hurt the balance of the tree by making the right subtree heavy

Binary Heap The implementation we will use is known as a binary heap. Like binary search trees,binary heaps have two properties,namely,a structure property and a heap order property
Binary Heap ◼ The implementation we will use is known as a binary heap. ◼ Like binary search trees, binary heaps have two properties, namely, a structure property and a heap order property
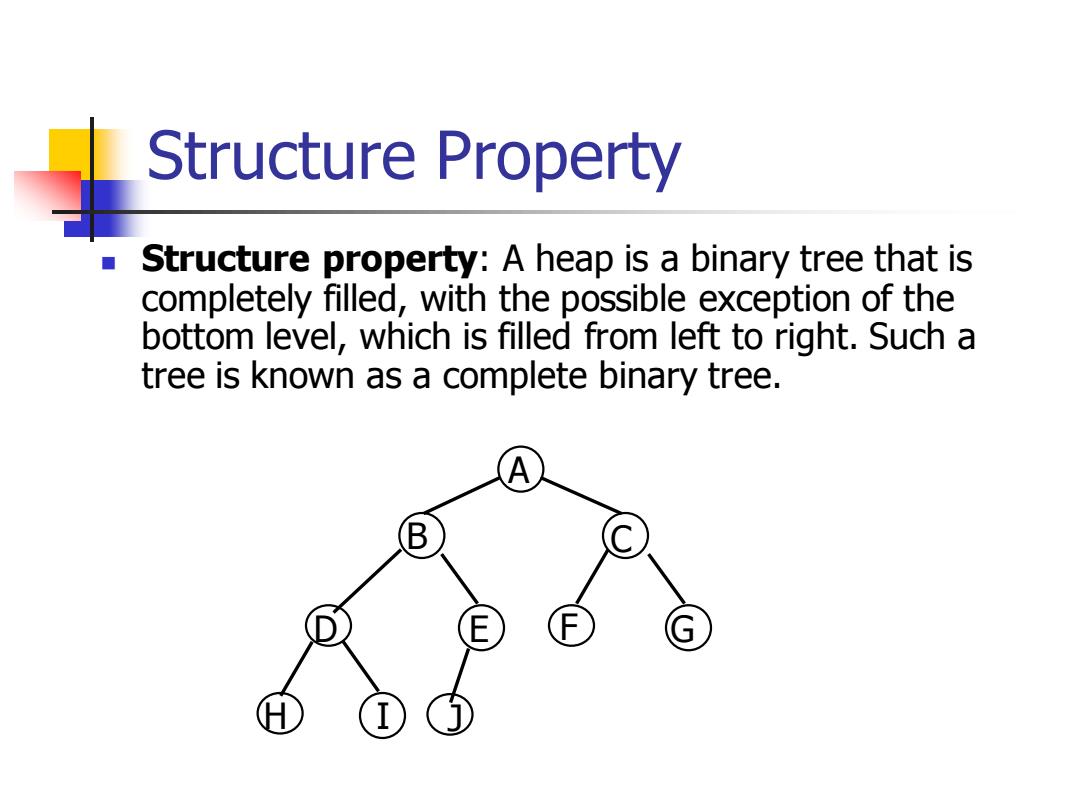
Structure Property Structure property:A heap is a binary tree that is completely filled,with the possible exception of the bottom level,which is filled from left to right.Such a tree is known as a complete binary tree. B E
Structure Property ◼ Structure property: A heap is a binary tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right. Such a tree is known as a complete binary tree. D E B C A F G H I J

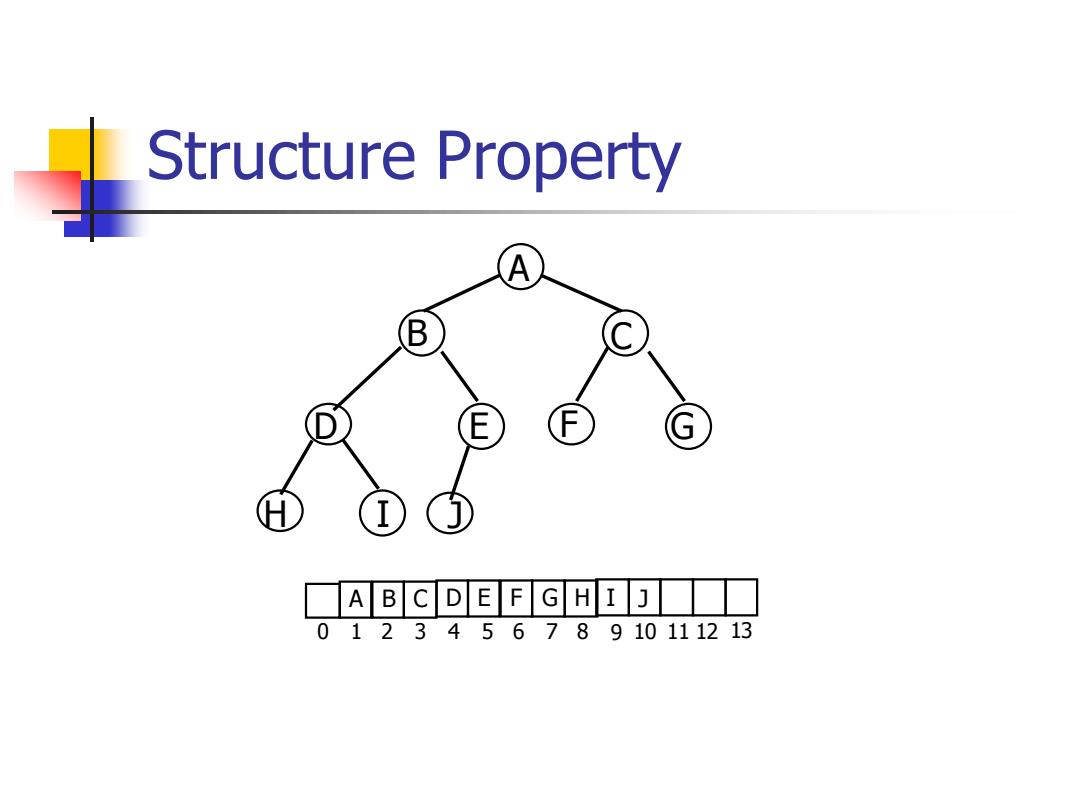
Structure Property An important observation is that because a complete binary tree is so regular,it can be represented in an array and no pointers are necessary. a For any element in array position /the left child is in position 2/the right child is in the cell after that left child (24+1),and the parent is in position L//2
Structure Property ◼ An important observation is that because a complete binary tree is so regular, it can be represented in an array and no pointers are necessary. ◼ For any element in array position i, the left child is in position 2i, the right child is in the cell after that left child (2i+1), and the parent is in position i/2
Structure Property A B E G A B CDE F GH I J 012345678910111213
Structure Property A B C D E F G H I J 0 1 2 3 4 5 6 7 8 9 10 11 12 13 D E B C A F G H I J

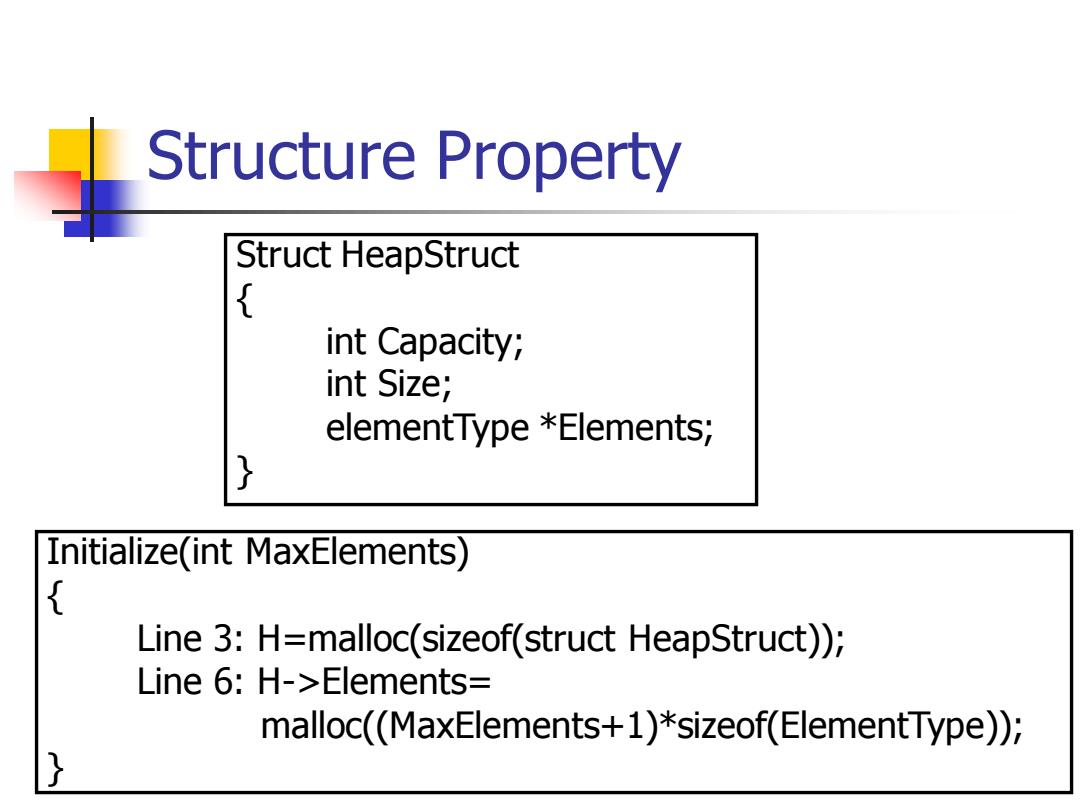
Structure Property Thus,not only are pointers not required,but the operations required to traverse the tree are extremely simple and likely to be very fast on most computers. The only problem with this implementation is that an estimate of the maximum heap size is required in advance. A heap data structure will then consist of an array (of whatever type the key is)and an integer representing the maximum and current heap sizes. Figure 6.4 shows a typical priority queue declaration
Structure Property ◼ Thus, not only are pointers not required, but the operations required to traverse the tree are extremely simple and likely to be very fast on most computers. ◼ The only problem with this implementation is that an estimate of the maximum heap size is required in advance. ◼ A heap data structure will then consist of an array (of whatever type the key is) and an integer representing the maximum and current heap sizes. ◼ Figure 6.4 shows a typical priority queue declaration
Structure Property Struct HeapStruct { int Capacity; int Size; elementType *Elements; Initialize(int MaxElements) { Line 3:H=malloc(sizeof(struct HeapStruct)); Line 6:H->Elements= malloc((MaxElements+1)*sizeof(ElementType)); }
Structure Property Struct HeapStruct { int Capacity; int Size; elementType *Elements; } Initialize(int MaxElements) { Line 3: H=malloc(sizeof(struct HeapStruct)); Line 6: H->Elements= malloc((MaxElements+1)*sizeof(ElementType)); }

Heap Order Property The property that allows operations to be performed quickly is the heap order property. Since we want to be able to find the minimum quickly, it makes sense that the smallest element should be at the root. If we consider that any subtree should also be a heap, then any node should be smaller than all of its descendants
Heap Order Property ◼ The property that allows operations to be performed quickly is the heap order property. ◼ Since we want to be able to find the minimum quickly, it makes sense that the smallest element should be at the root. ◼ If we consider that any subtree should also be a heap, then any node should be smaller than all of its descendants