
Iterative Improvement for Domain-Specific Problems Lecturer:Jing Liu Email:neouma@mail.xidian.edu.cn Homepage:http://see.xidian.edu.cn/faculty/liujing
Iterative Improvement for Domain-Specific Problems Lecturer: Jing Liu Email: neouma@mail.xidian.edu.cn Homepage: http://see.xidian.edu.cn/faculty/liujing

Iterative Improvement for Domain-Specific Problems In this part,we will study an algorithm design technique that we will refer to as iterative improvement. In its simplest form,this technique starts with a simple-minded (usually a greedy)solution and continues to improve on that solution in stages until an optimal solution is found. Finding a maximum flow in a network >Finding a maximum matching in undirected graphs
Iterative Improvement for Domain-Specific Problems ◼ In this part, we will study an algorithm design technique that we will refer to as iterative improvement. ◼ In its simplest form, this technique starts with a simple-minded (usually a greedy) solution and continues to improve on that solution in stages until an optimal solution is found. ➢ Finding a maximum flow in a network ➢ Finding a maximum matching in undirected graphs

Network Fow A network is a 4-tuple (G,s,t,c),where G=(,E)is a directed graph,s and tare two distinguished vertices called,respectively,the source and sink,and du,is a capacity function defined on all pairs of vertices with du,v)>0 if (u,veFand du,v)=0 otherwise.=n,=m. Next,we consider the problem of finding a maximum flow in a given network (G,s,t,c)from sto t,which is named as the max-flow problem
Network Flow ◼ A network is a 4-tuple (G, s, t, c), where G=(V, E) is a directed graph, s and t are two distinguished vertices called, respectively, the source and sink, and c(u, v) is a capacity function defined on all pairs of vertices with c(u, v)>0 if (u, v)E and c(u, v)=0 otherwise. |V|=n, |E|=m. ◼ Next, we consider the problem of finding a maximum flow in a given network (G, s, t, c) from s to t, which is named as the max-flow problem

Network Flow A fow in Gis a real-valued function fon vertex pairs having the following four conditions: (1)Skew symmetry.vu,velu,=-v).We say there is a flow from uto vif,>0. (2)Capacity constraints.Vu,veV,u,vsdu,v. We say edge (u,v)is saturated if u,=du,v). (3)Flow conservation.Vue s,veu,v)=0.In other words,the net fow(total flow out minus total flow in)at any interior vertex is 0. (4)廿vEVy)=0
Network Flow A flow in G is a real-valued function f on vertex pairs having the following four conditions: (1) Skew symmetry. u, vV, f(u, v)=-f(v, u). We say there is a flow from u to v if f(u, v)>0. (2) Capacity constraints. u, vV, f(u, v)c(u, v). We say edge (u, v) is saturated if f(u, v)=c(u, v). (3) Flow conservation. uV-{s, t}, vV f(u, v)=0. In other words, the net flow (total flow out minus total flow in) at any interior vertex is 0. (4) vV, f(v, v)=0

Network Fow A cut is,n is a partition of the vertex set Vinto two subsets Sand Tsuch that seS and te 7.The capacity of the cut{S,乃,denoted by d(S,T),is c(S,T)=∑c(4,) UES,VET The flow across the cut{S,刀,denoted by(S,刀,is f(S,T)=∑f(u,) 1l∈S,veT Thus,the flow across the cut is,n is the sum of the positive flow on edges from Sto Tminus the sum of the positive flow on edges from Tto S
Network Flow ◼ A cut {S, T} is a partition of the vertex set V into two subsets S and T such that sS and tT. The capacity of the cut {S, T}, denoted by c(S, T), is , ( , ) ( , ) u S v T c S T c u v = ◼ The flow across the cut {S, T}, denoted by f(S, T), is , ( , ) ( , ) u S v T f S T f u v = ◼ Thus, the flow across the cut {S, T} is the sum of the positive flow on edges from S to T minus the sum of the positive flow on edges from T to S

Network F ow ● For any vertex uand any subset AcV,let fu,A) denote fu,A),and 4 u)denote A,u).For a capacity function c du,A)and dA,u)are defined similar. The value of a flow f denoted by f,is defined to be If=f(s,)=∑f(s,v) Lemma:For any cut {S,D and a flow,7). Max-Flow Problems:Design a function f for the network(G,s,t,c),so that f is the maximum
◼ For any vertex u and any subset AV, let f(u, A) denote f({u}, A), and f(A, u) denote f(A, {u}). For a capacity function c, c(u, A) and c(A, u) are defined similar. ◼ The value of a flow f, denoted by |f|, is defined to be Network Flow | | ( , ) ( , ) v V f f s V f s v = = ◼ Lemma: For any cut {S, T} and a flow f, |f|=f(S, T). ◼ Max-Flow Problems: Design a function f for the network (G, s, t, c), so that |f| is the maximum

Network Fow Given a flow fon Gwith capacity function c the residual capacity function for fon the set of pairs of vertices is defined as follows. ◆ For each pair of vertices,u,ve v,the residual capacity ru v)=du,v-fu,v).The residual graph for the flow is the directed graph R=(,E),with capacities defined by rand E={(山,小(u,>0 ◆ The residual capacity /(u,v represents the amount of additional flow that can be pushed along the edge (u,v without violating the capacity constraints. If fu,v<du,v),then both (u,v)and (v,u)are present in R.If there is no edge between wand vin G,then neither (u,v)nor (v,u)are in E Thus,2E
◼ Given a flow f on G with capacity function c, the residual capacity function for f on the set of pairs of vertices is defined as follows. ◼ For each pair of vertices, u, vV, the residual capacity r(u, v)=c(u, v)-f(u, v). The residual graph for the flow f is the directed graph R=(V, Ef ), with capacities defined by r and Ef={(u, v)|r(u, v)>0} ◼ The residual capacity r(u, v) represents the amount of additional flow that can be pushed along the edge (u, v) without violating the capacity constraints. ◼ If f(u, v)<c(u, v), then both (u, v) and (v, u) are present in R. If there is no edge between u and v in G, then neither (u, v) nor (v, u) are in Ef . Thus, |Ef |2|E|. Network Flow
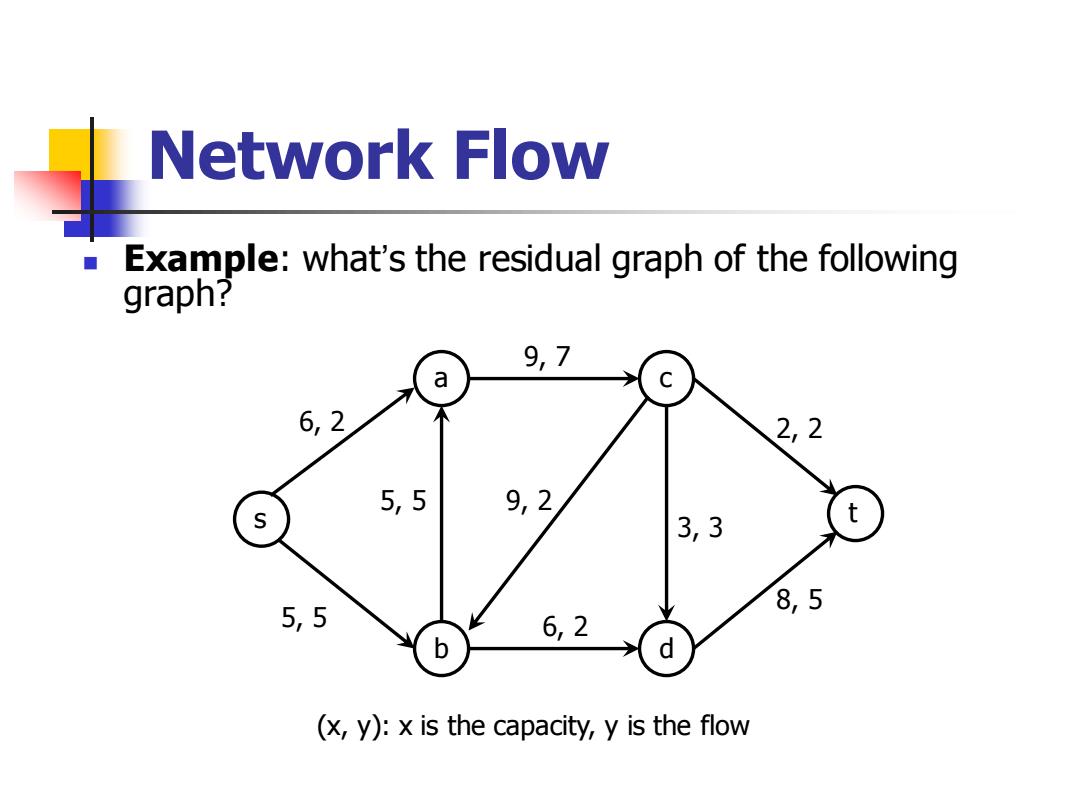
Network Flow Example:what's the residual graph of the following graph? 9,7 a 6,2 2,2 5,5 9,2 s 3,3 t 5,5 8,5 6,2 b (x,y):x is the capacity,y is the flow
◼ Example: what’s the residual graph of the following graph? Network Flow s a b c d t 6, 2 5, 5 5, 5 9, 7 9, 2 6, 2 3, 3 2, 2 8, 5 (x, y): x is the capacity, y is the flow

Network Fow Let fand f'be any two flows in a network G.Define the function ff'by (A')(u,v)=u,v)+f'(u,v)for all pairs of vertices u and v.Similarly,define the function Ff'by(ff'(u,)=u,Wf'(山,). Lemma:Let fbe a flow in Gand f'the flow in the residual graph R for f.Then the function Af'is a flow in Gof value +f'. Lemma:Let fbe any flow in Gand f*a maximum flow in G.If R is the residual graph for then the value of a maximum flow in R is f*-f
◼ Let f and f ’ be any two flows in a network G. Define the function f+f ’ by (f+f ’)(u, v)=f(u, v)+f ’(u, v) for all pairs of vertices u and v. Similarly, define the function f-f ’ by (f-f ’)(u, v)=f(u, v)-f ’(u, v). ◼ Lemma: Let f be a flow in G and f ’ the flow in the residual graph R for f. Then the function f+f ’ is a flow in G of value |f|+|f ’|. ◼ Lemma: Let f be any flow in G and f * a maximum flow in G. If R is the residual graph for f, then the value of a maximum flow in R is |f * |-|f|. Network Flow

Network F ow Given a flow fin G,an augmenting path p is a directed path from s to tin the residual graph R.The bottleneck capacity of p is the minimum residual capacity along p.The number of edges in p will be denoted by |p. Theorem (max-flow min-cut theorem):Let (G,s t,c)be a network and fa flow in G.The following three statements are equivalent: (a)There is a cut{S,乃with(S,T刀=li. (b)fis a maximum flow in G. (c)There is no augmenting path for f
◼ Given a flow f in G, an augmenting path p is a directed path from s to t in the residual graph R. The bottleneck capacity of p is the minimum residual capacity along p. The number of edges in p will be denoted by |p|. ◼ Theorem (max-flow min-cut theorem): Let (G, s, t, c) be a network and f a flow in G. The following three statements are equivalent: (a) There is a cut {S, T} with c(S, T)=|f|. (b) f is a maximum flow in G. (c) There is no augmenting path for f. Network Flow