
4组合逻辑电路 Combinational Logic Circuits 4.0引言(Introduction) 4.1组合逻辑电路的分析(Analysis) 4.2组合逻辑电路的设计(Design) 4.3组合逻辑电路中的竟争冒险 4.4典型的组合逻辑集成电路 4.5组合可编程逻辑器件(PLD)
4.1 组合逻辑电路的分析(Analysis ) 4.2 组合逻辑电路的设计(Design) 4.4 典型的组合逻辑集成电路 4.3 组合逻辑电路中的竟争冒险 4.0 引言(Introduction) 4 组合逻辑电路 Combinational Logic Circuits 4.5 组合可编程逻辑器件(PLD)
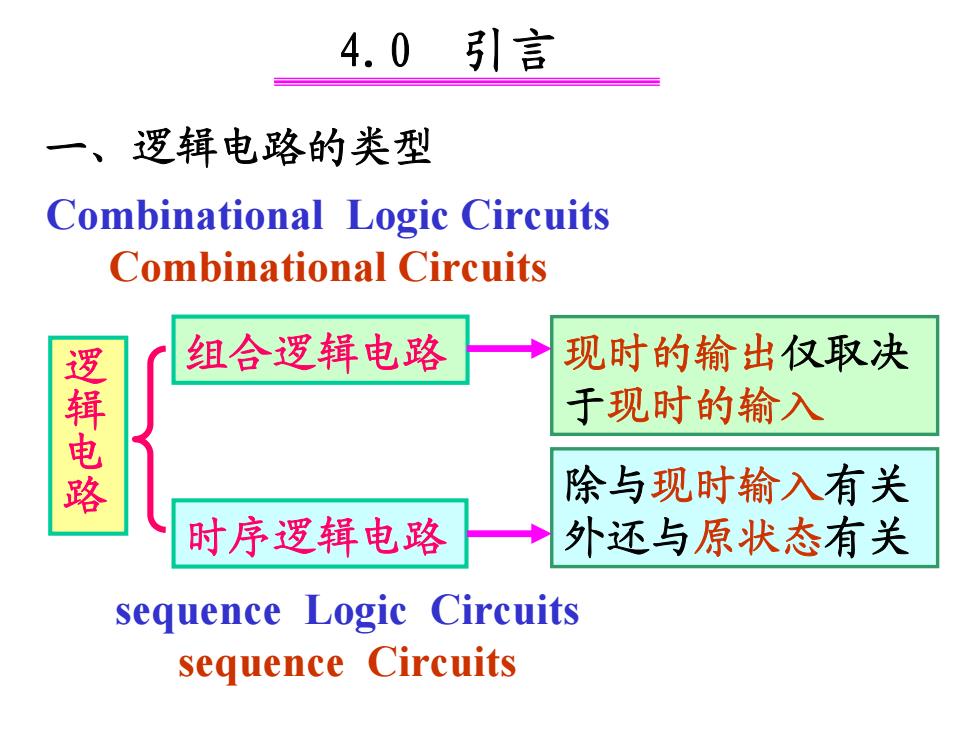
4.0引言 一、 逻辑电路的类型 Combinational Logic Circuits Combinational Circuits 组合逻辑电路 现时的输出仅取决 逻辑电路 于现时的输入 除与现时输入有关 时序逻辑电路 外还与原状态有关 sequence Logic Circuits sequence Circuits
4.0 引言 逻辑电路 组合逻辑电路 时序逻辑电路 现时的输出仅取决 于现时的输入 除与现时输入有关 外还与原状态有关 Combinational Logic Circuits Combinational Circuits sequence Logic Circuits sequence Circuits 一、逻辑电路的类型

二、组合电路与时序电路的特点 1.Combinational circuits(组合电路) The output level is dependent on the present input levels.(输出仅决定于输入) ◆No storage element.(储存单元) ◆No Feedback.(反馈) 2.Sequential circuits(时序电路) The output level depends not only on the present value of inputs,but also on past inputs. Employ storage element ◆Feedback involved
二、组合电路与时序电路的特点 1. Combinational circuits(组合电路) ◆The output level is dependent on the present input levels.(输出仅决定于输入) ◆ No storage element. (储存单元) 2. Sequential circuits(时序电路) ◆ The output level depends not only on the present value of inputs, but also on past inputs. ◆ Employ storage element ◆ No Feedback.(反馈) ◆ Feedback involved
三、组合电路与时序电路的组成框图 Input Logic gates Output Input Outpu 组合电路 组合电路 Block Diagram of Memory Combinationl Circuits Q Block diagram of ◆组合电路 Sequential circuits L:=f(A1,A2,An)) Q”为输入信号作用之前的状态 ◆时序电路 Q+1为输入信号作用之后的状态 Zk=fi(X,X2,.,X,2”,22,2")(k=1~边 2=f1(Y,Y2,.,Y,2,22,.,2,)0=1~)
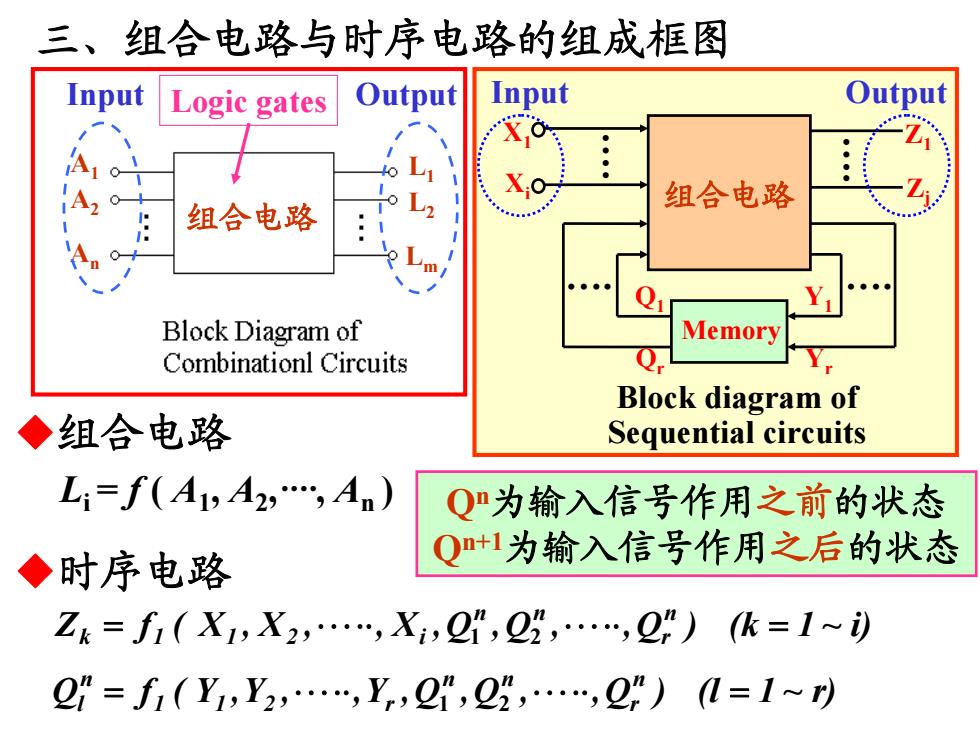
A1 A2 An L1 L2 Lm 组合电路 组合电路 Memory Block diagram of Sequential circuits . . . . X1 Xi Z1 Zj Q1 Qr Y1 Yr 三、组合电路与时序电路的组成框图 Input Logic gates Output Input Output ◆组合电路 Li = f ( A1 , A2 ,····, An ) ◆时序电路 i)~1(k )Q , ,Q ,Q ,X , ,X ,X ( fZ nr nn 211k i 21 r)~1(l )Q , ,Q ,Q ,Y , ,Y ,Y ( fQ nr nn 211 r nl 21 Qn为输入信号作用之前的状态 Qn+1为输入信号作用之后的状态

四、组合逻辑电路的分析与设计 Combinational Circuits Analysis Design 组合电路的设计(Design) 逻辑问题亡真值表逻辑表达式逻辑图 组合电路的分析(Analysis) ◆组合电路的分析:给定电路,要求确定其逻辑 功能;或验证已知电路逻辑功能的正确性. ◆组合电路的设计:给定逻辑功能的要求或逻辑 函数,设计能完成该功能的最简的逻辑电路
◆组合电路的分析:给定电路,要求确定其逻辑 功能;或验证已知电路逻辑功能的正确性. 逻辑问题 真值表 逻辑表达式 逻辑图 组合电路的设计(Design) 组合电路的分析(Analysis) ◆组合电路的设计:给定逻辑功能的要求或逻辑 函数,设计能完成该功能的最简的逻辑电路. 四、组合逻辑电路的分析与设计 Combinational Circuits Analysis & Design

4.1组合逻辑电路的分析 Combinational Circuits Analysis Analysis Procedure 逻辑图→表达式→化简→真值表→逻辑功能 1.由给定的逻辑图逐级写出逻辑表达式; 2.化简逻辑表达式式,得出最简与或表达式; 化简方法:公式化简法和卡诺图法 3.列出真值表,分析真值表得到逻辑功能
1.由给定的逻辑图逐级写出逻辑表达式; 2.化简逻辑表达式式,得出最简与或表达式; 3.列出真值表,分析真值表得到逻辑功能。 化简方法:公式化简法和卡诺图法 逻辑图 表达式 化简 真值表 逻辑功能 Analysis Procedure 4.1 组合逻辑电路的分析 Combinational Circuits Analysis
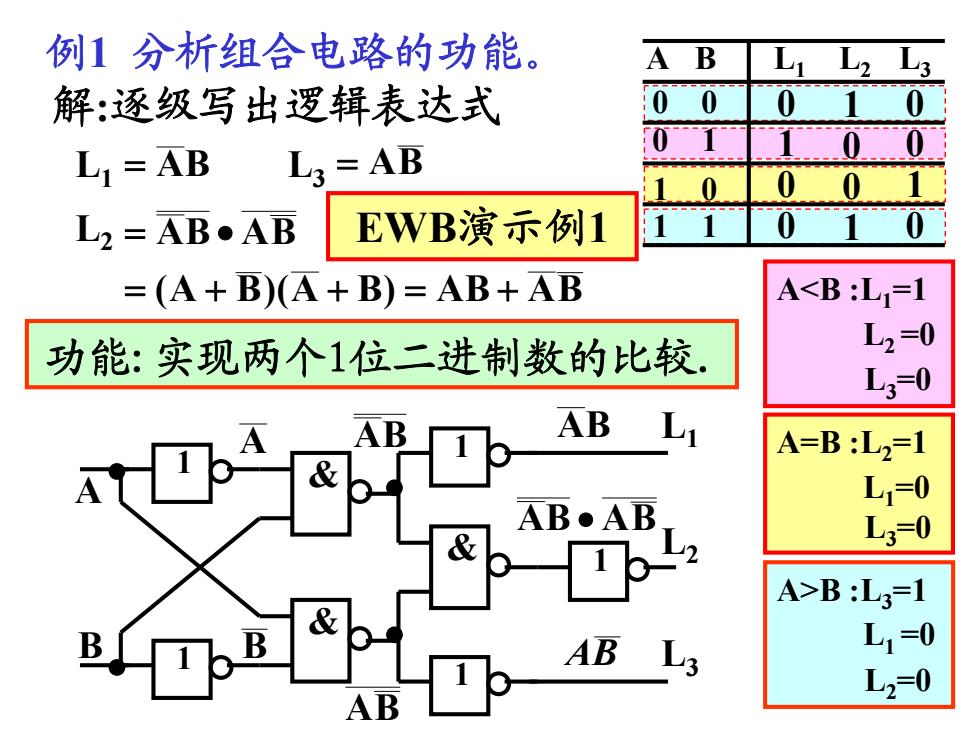
例1分析组合电路的功能。 A B 解:逐级写出逻辑表达式 0 0 L=AB L3=AB 0 0 L2=AB●AD EWB演示例1 =(A+B)(A+B)=AB+AB AB:L3=1 AB L1=0 L2=0 AB
AB :L3 =1 L1 =0 L2 =0 例1 分析组合电路的功能。 1 & 1 1 1 1 & & • • • • A B L1 L3 L2 A B BA BA BA AB BABA 解:逐级写出逻辑表达式 L1 BA L3 BA L2 BABA BAAB)BA)(BA( 0 0 A B L1 L2 L3 0 1 1 0 1 1 0 1 0 1 0 0 0 0 1 0 1 0 功能:实现两个1位二进制数的比较. EWB演示例1
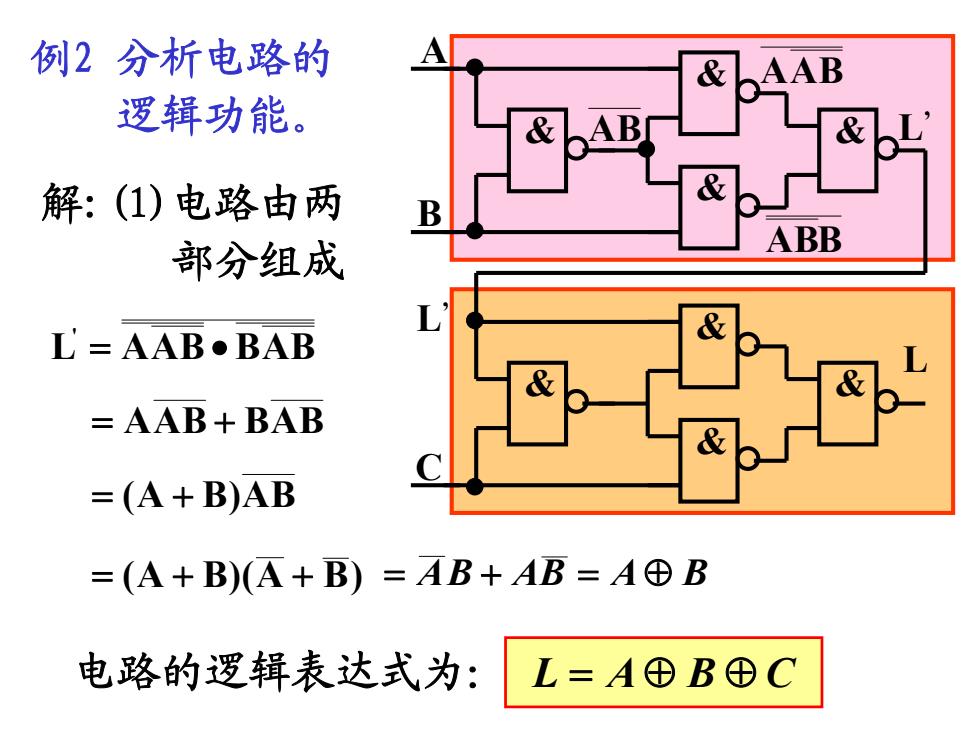
例2分析电路的 AAB 逻辑功能。 解:(1)电路由两 部分组成 ABB L E=AAB·BAB =AAB+BAB =(A+B)AB =(A+B)(A+B)=4B+AB=AB 电路的逻辑表达式为:L=A田B⊕C
L & L’ & & & & & & & A B C L’ 例2 分析电路的 逻辑功能。 解:(1)电路由两 部分组成 L AAB BAB ' AAB BAB (A B)AB (A B)(A B) AB AB A B AB AAB ABB 电路的逻辑表达式为: L A B C
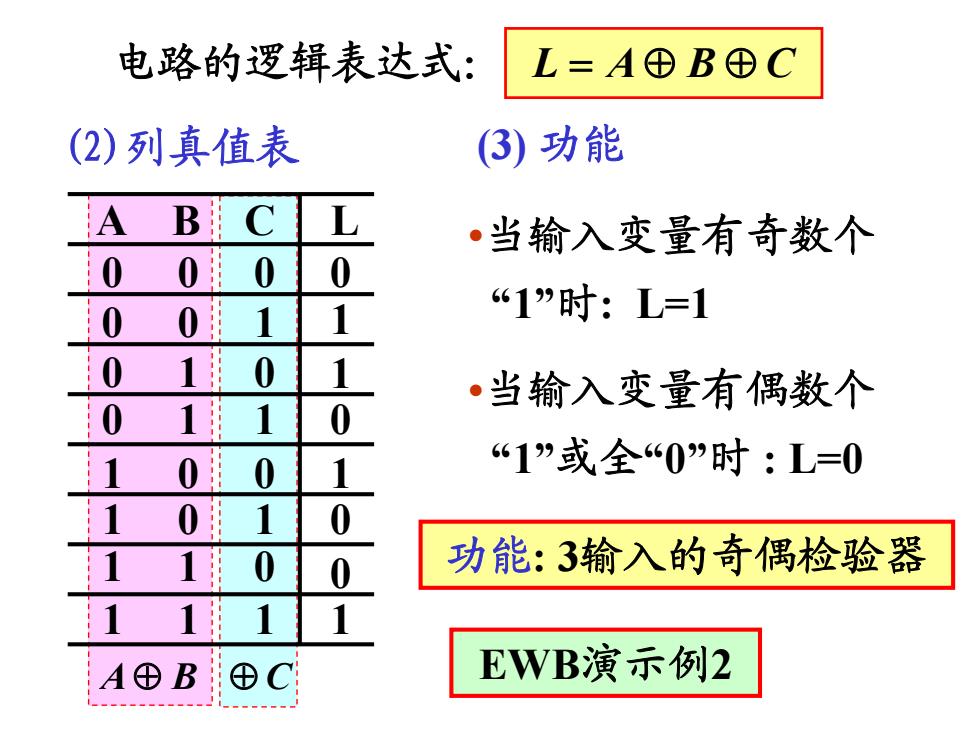
电路的逻辑表达式: L=A⊕B⊕C (2)列真值表 (3)功能 A B L ·当输入变量有奇数个 0 0 0 0 0 0 1 61”时:L=1 0 ·当输入变量有偶数个 0 1 “1”或全“0”时:L=0 0 0 功能:3输入的奇偶检验器 A⊕B ⊕C EWB演示例2
A B C 0 0 0 0 1 1 1 1 A B C L 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 •当输入变量有奇数个 “1”时: L=1 •当输入变量有偶数个 “1”或全“0”时 : L=0 (2)列真值表 (3) 功能 电路的逻辑表达式: L A CB 功能: 3输入的奇偶检验器 EWB演示例2
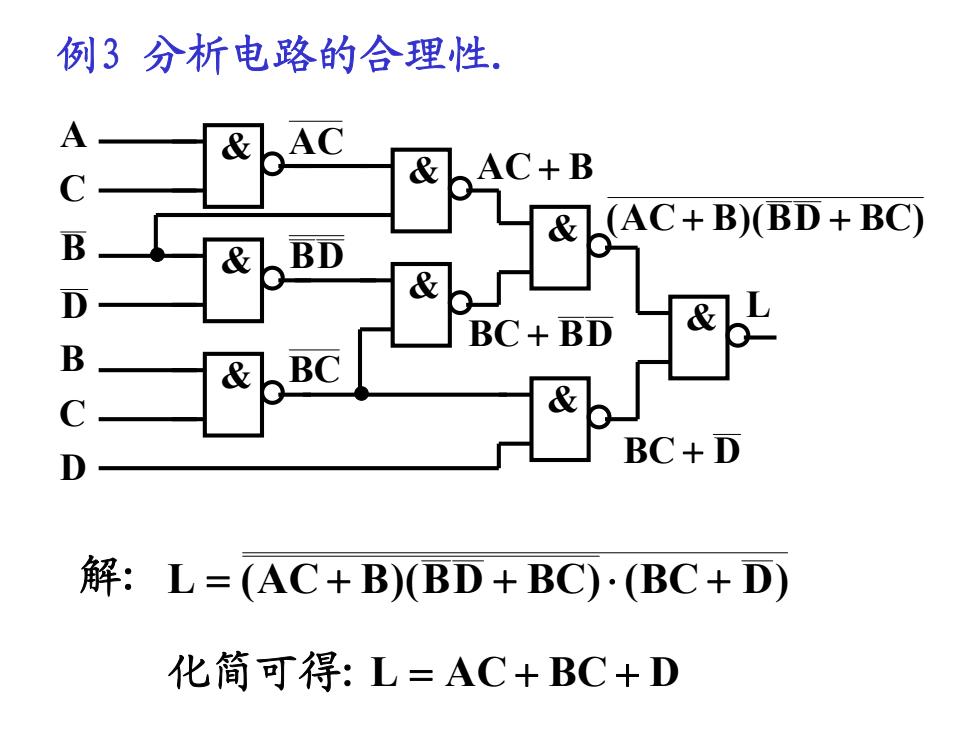
例3分析电路的合理性. A 。AC AC+B C & &AC+B)(BD+BC) B & BD D & BC+BD & B BC C & BC+D D 解:L=(AC+B)BD+BC)(BC+D) 化简可得:L=AC+BC+D
AC DB BC BAC DBBC DBC )BCDB)(BAC( & & & & & & & & A C B D B C D L 例3 分析电路的合理性. 解: )DBC()BCDB)(BAC(L 化简可得: DBCACL