
2逻辑代数基础 Boolean algebra (Logic algebra) 2.0 引言(Introduction) 2.1 逻辑代数(Boolean Algebra) 2.2 ?逻辑函数的卡诺图化简 2.3 硬件描述语言(HDL)基础
2.1 逻辑代数(Boolean Algebra) 2.2 逻辑函数的卡诺图化简 2.3 硬件描述语言(HDL)基础 2.0 引言(Introduction) 2 逻辑代数基础 Boolean algebra (Logic algebra)

2.0引言 ◆Logic Function Logic Function is a tool to describe the relationship between a logic circuit's output(s) and its input(s):L=f (A,B,C,.). *Two possible values:0 or 1.Logic 0 and Logic 1 don't present actual numbers but present two states that are contradictory to each other. Describe a Logic function Truth table logic equation Logic diagram Karnaugh maps waveform
2.0 引言 ◆ Describe a Logic function Describe a Logic function * Truth table * logic equation * Logic diagram * Karnaugh maps * waveform ◆ Logic Function * Logic Function is a tool to describe the relationship between a logic circuit’s output(s) and its input(s): L = f(A,B,C,.). *Two possible values:0 or 1. Logic 0 and Logic 1 don’t present actual numbers but present two states that are contradictory to each other
◆Key words *Boolean/Logic Algebra(布尔/逻辑代数) *Logic Function(逻辑函数) *AND(与)、OR(或)、NOT(非) *NAND(与非)、NOR(或非) *EXCLUSIVE-OR(异或) Truth Table (真值表) *Karnaugh Map(卡诺图) *Logic Circuits/Logic diagram(逻辑电路) *waveform(波形图)
◆Key words Key words * Boolean/Logic Algebra (布尔/逻辑代数) * Logic Function (逻辑函数) * AND (与) 、OR (或) 、NOT (非) * NAND (与非)、NOR (或非) * EXCLUSIVE-OR (异或) * Truth Table (真值表) * Karnaugh Map (卡诺图) * Logic Circuits/Logic diagram (逻辑电路) *waveform (波形图)

2.1逻辑代数(Boolean Algebra), 逻辑代数:又称布尔代数,是分析与设计 逻辑电路的工具。逻辑代数表示的是逻辑关 系,它的变量取值只有1和0,表示两个相反 的逻辑关系。 基本逻辑运算:与、或、非逻辑运算。 一、逻辑代数的基本运算规则 或运算:A+0=A,A+1=1,A+A=A,A+A=1 与运算:A.0=0,A1=A,A·A=A,AA=0 非运算:A=A
2.1 逻辑代数(Boolean Algebra ) 逻辑代数: 又称布尔代数, 是分析与设计 逻辑电路的工具。逻辑代数表示的是逻辑关 系,它的变量取值只有 1 和 0,表示两个相反 的逻辑关系。 基本逻辑运算:与、或、非逻辑运算。 一、逻辑代数的基本运算规则 或运算: 11 0 AA,AAA,A,AA 1 与运算 : AA,AAA,AA,A 0 1 00 非运算: A A

二、逻辑代数的基本定律 ◆交换律(Commutative Law): A+B=B+A,A·B=B·A ◆结合律(Associative Law): A+(B+C=(A+B)+C,A·B·C=A·B)·C ◆分配律(Distributive Law): AB+C=A·B+A·C,A+B·C=(A+B)·A+C ◆摩根定律(DeMorgan's theorem): A●B=A+B A+B=A●B ◆吸收定律(Absorptive Law): A+AB-A+B,A+AB-A ◆包含律(Inclusive Law): AB+AC+BC=AB+AC
二、逻辑代数的基本定律 ◆结合律(Associative Law ) : A+(B+C)=(A+B)+C ,A • (B • C)=(A • B) • C ◆吸收定律(Absorptive Law): A+AB=A+B , A+AB=A ◆分配律(Distributive Law): A(B+C)=A • B+A • C , A+B • C=(A+B) • (A+C) ◆交换律(Commutative Law ) : A+B=B+A , A • B=B • A BABABABA ( s'DeMorgan ◆摩根定律 : theorem) ◆包含律(Inclusive Law ) : A B A C C ABB A C
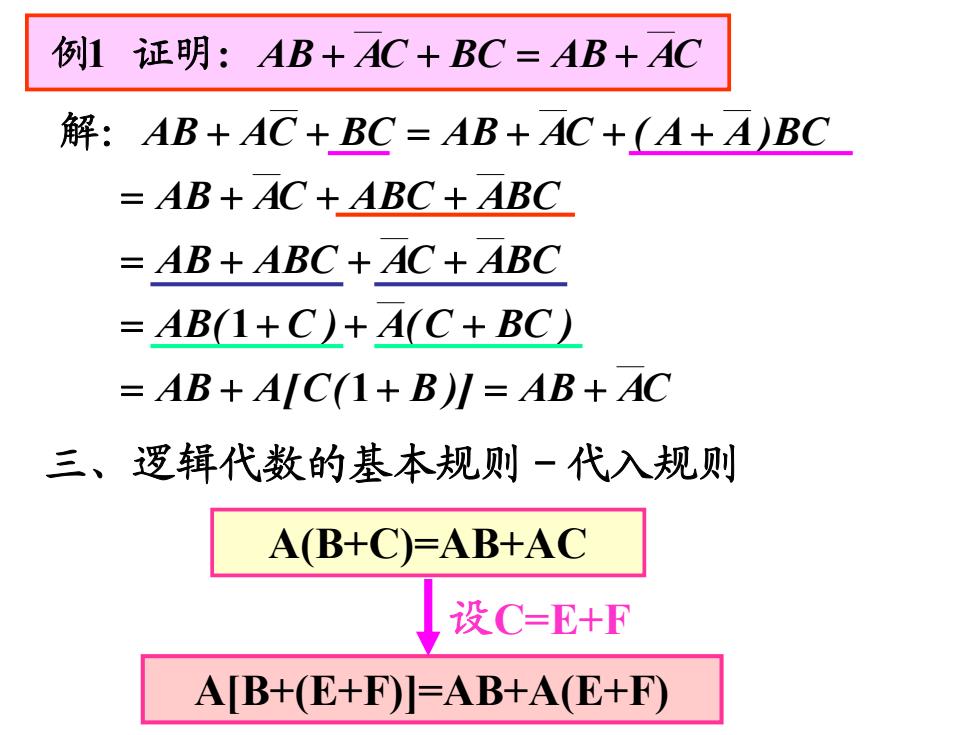
例1证明:AB+AC+BC=AB+AC 解:AB+AC+BC=AB+AC+(A+A)BC =AB+AC+ABC+ABC =AB+ABC+AC+ABC AB(1+C)+A(C+BC) =AB+AC(1+B)川=AB+AC 三、逻辑代数的基本规则-代入规则 A(B+C)=AB+AC 设C=E+F A[B+(E+F)=AB+AE+F)
例 证明 : 1 AB AC C ABB AC CAAB)]B(C[AAB )BCC(A)C(AB BCACAABCAB BCAABCCAAB BC)AA(CAABBCCAAB 1 1 解: 三、逻辑代数的基本规则-代入规则 A(B+C)=AB+AC A[B+(E+F)]=AB+A(E+F) 设C=E+F
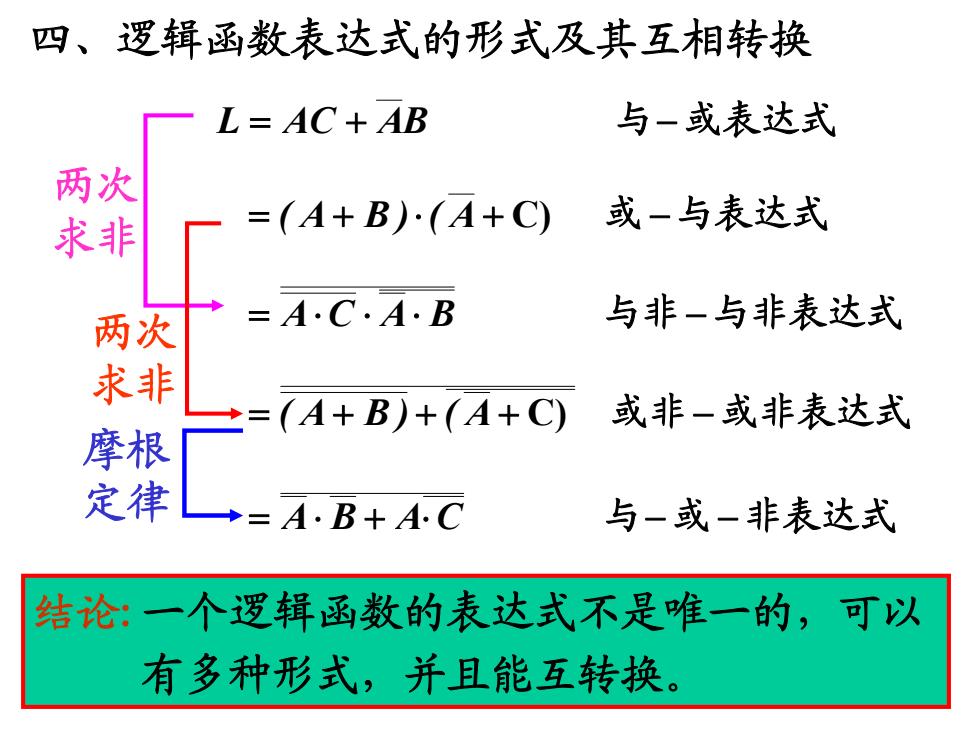
四、逻辑函数表达式的形式及其互相转换 飞工=AC+AB 与-或表达式 两次 求非 =(A+B)(A+C) 或一与表达式 两次 :AC·A·B 与非一与非表达式 求非 ◆ =(A+B)+(A+C) 或非一或非表达式 摩根 定律 →=A.B+AC 与一或一非表达式 结论:一个逻辑函数的表达式不是唯一的,可以 有多种形式,并且能互转换
四、逻辑函数表达式的形式及其互相转换 结论:一个逻辑函数的表达式不是唯一的,可以 有多种形式,并且能互转换。 L AC AB 与 或表达式 A()BA( C) 或 与表达式 A B AC 或与 非表达式 摩根 定律 AC A B 与非 与非表达式 两次 求非 A()BA( C) 或非 或非表达式 两次 求非

五、逻辑函数的代数法化简(Simplification) 化简方法 T代数法(Algebraic) Simplification method L卡诺图法(Karnaugh Map) 1、化简的目的 √电路所用的逻辑门数量尽量少一节省器件 Use logic gates as less as possible. √各逻辑门的输入端尽量少一减少连线 Inputs of one gate are as less as possible. √电路的级数尽量少一提高工作速度 The stages of the logic circuit is as less as possible. √电路的可靠性尽可能高 The reliability of the logic circuits is as high as possible
五、逻辑函数的代数法化简 (Simplification ) 1、化简的目的 电路所用的逻辑门数量尽量少 —节省器件 各逻辑门的输入端尽量少 —减少连线 电路的级数尽量少 —提高工作速度 化简方法 Simplification method 代数法 (Algebraic ) 卡诺图法 (Karnaugh Map ) Use logic gates as less as possible. Inputs of one gate are as less as possible. The stages of the logic circuit is as less as possible 。 The reliability of the logic circuits is as high as possible. 电路的可靠性尽可能高
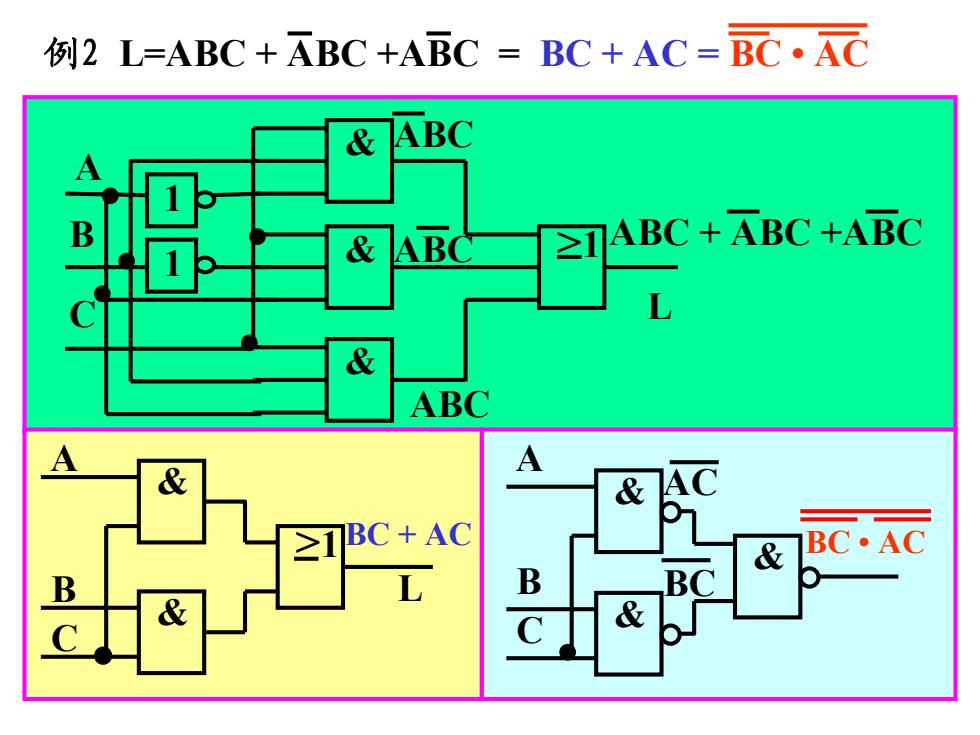
例2L=ABC+ABC+ABC=BC+AC=BC·AC & ABC & ≥1 ABC+ABC +ABC & ABC A BC·AC B
• & & & >1 1 1 • • • • ABC + ABC +ABC ABC ABC ABC A B C L & & >1 • BC + AC L A B C • & & A & B C BC • AC AC BC 例2 L=ABC + ABC +ABC = BC + AC = BC • AC

2、最简与一或表达式:最基本的表达式 ◆乘积项项数最少 (With less products in the expression) ◆每个乘积项中变量个数最少 (With less variables in the products) L-ABC+ABC+ABC BC+AC 非最简与一或表达式最简与一或表达式 Simplification 3、逻辑函数的代数法化简 利用逻辑代数的基本公式、定律进行化简。 方法有并项法、消项法、消元法和配项法
非最简与—或表达式 最简与—或表达式 2、最简与—或表达式:最基本的表达式 ◆乘积项项数最少 (With less products in the expression) ◆每个乘积项中变量个数最少 (With less variables in the products) L= ABC + ABC +ABC = BC + AC 3、逻辑函数的代数法化简 利用逻辑代数的基本公式、定律进行化简。 方法有并项法、消项法、消元法和配项法。 Simplification