
先进控制理论与控制工程 中圆地质大学自动化学院吴敏 第三讲: 时滞系统鲁棒控制 79 2021年9月13日
79 2021年9月13日 时滞系统鲁棒控制 第三讲: 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中固地质大芳自动化学院吴敏 时滞系统鲁棒控制 研究背景 时滞相关鲁棒控制方法 > 全新的自由权矩阵方法 > 时滞相关稳定性分析 改进的自由权矩阵方法 80 2021年9月13日
80 2021年9月13日 时滞系统鲁棒控制 研究背景 时滞相关鲁棒控制方法 全新的自由权矩阵方法 时滞相关稳定性分析 改进的自由权矩阵方法 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中固地质大学 自动化学院吴敏 研究背景 >工业过程控制中的时滞问题 ◆温度控制中的时延(如加热炉、炼焦生产过程、铁矿旷石和有色金属矿 烧结过程、高炉等) ◆如何克服时滞来保证控制系统性能 ◆如何利用时滞环节来提高控制系统性能 >冶金工业过程 大型互联电网 >网络控制系统 ✉目是是= 品 81 2021年9月13日
81 2021年9月13日 研究背景 工业过程控制中的时滞问题 温度控制中的时延(如加热炉、炼焦生产过程、铁矿石和有色金属矿 烧结过程、高炉等) 如何克服时滞来保证控制系统性能 如何利用时滞环节来提高控制系统性能 冶金工业过程 大型互联电网 网络控制系统 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 时滞系统控制问题 >时滞系统建模问题:如何描述时滞系统 >时滞无关与时滞相关 (t)=Ax(t)+Adx(t-h) (1) (=(A+A)x() (2) ◆ 当=0时,系统(1)就是系统(2)。 设系统(2)稳定,根据连续性,当很小时系统(1)稳定, 但并非对任意>0都是稳定的。 82 2021年9月13日
82 2021年9月13日 时滞系统控制问题 时滞系统建模问题:如何描述时滞系统 当h=0时,系统(1)就是系统(2)。 设系统(2)稳定,根据连续性,当h很小时系统(1)稳定, 但并非对任意h>0都是稳定的。 ( ) ( ) ( ) (2) ( ) ( ) ( ) (1) x t A A x t x t Ax t A x t h d d - 时滞无关与时滞相关 先进控制理论与控制工程 吴 敏
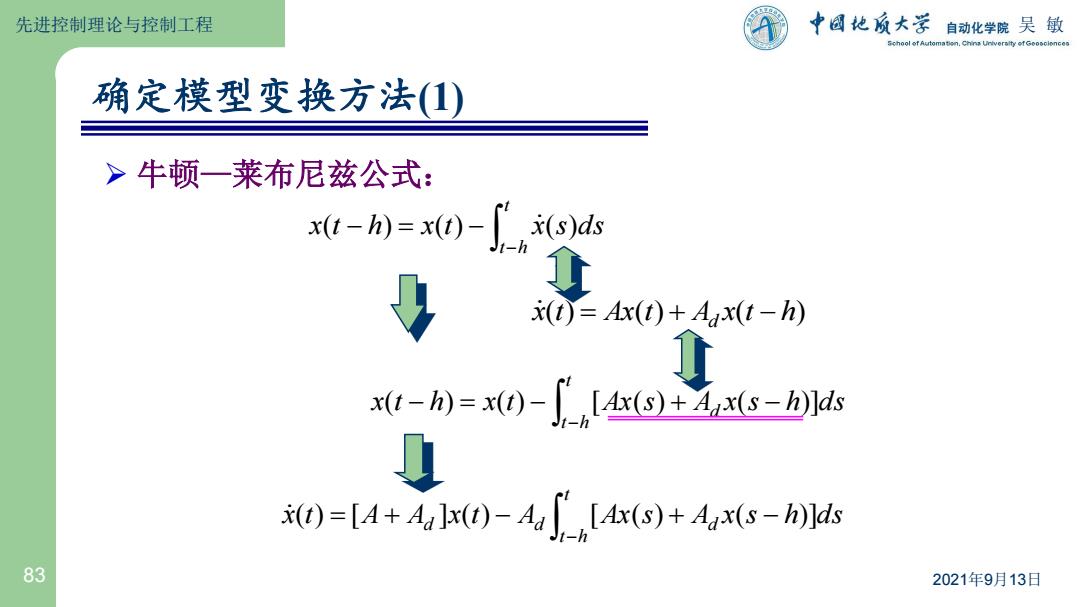
先进控制理论与控制工程 中国地质大学自动化学院吴敏 确定模型变换方法(1) >牛顿一莱布尼兹公式: xt-M=x0-∫ss (t)=Ax(t)+Aux(t-h) ① x(t-h)=x(t)-[LAx(s)+Ajx(s-h)]ds 0 ()=[4+Au kx()-Aa [Ax(s)+Aax(s-h)lds 83 2021年9月13日
83 2021年9月13日 - - - t t h x(t) [A Ad ]x(t) Ad [Ax(s) Ad x(s h)]d s 确定模型变换方法(1) 牛顿—莱布尼兹公式: - - - t t h x(t h) x(t) x(s)ds x(t) Ax(t) A x(t h) d - - - - - t t h x(t h) x(t) [Ax(s) Ad x(s h)]ds 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆枕质大学自动化学院吴敏 确定模型变换方法(2) >四种基本的确定模型变换 ()=[4+Aa lx()-Aa [Ax(s)+Aax(s-h)lds () x0+4ss=(4+Ak0 局限性: 有附加特征值,与原系统不等价; 使用的不等式有很大的保守性: 2ab≤aRa+bR-b,R>0 84 2021年9月13日
84 2021年9月13日 四种基本的确定模型变换 - - - t t h (I) x(t) [A Ad ]x(t) Ad [Ax(s) Ad x(s h)]d s (II) [x(t) A x(s)]d s (A A )x(t) d t d t t h d d - 局限性: 有附加特征值,与原系统不等价; 使用的不等式有很大的保守性: 2 , 0 1 - a b a Ra b R b R T T T 确定模型变换方法(2) 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆地质大学自动化学院吴敏 确定模型变换方法(3) (Ⅲ) Park Moon:)=[4+4alx()-Aa[(s)ds (t)=y(t) (IV)Fridman: ()=[4+A)-4i[()ds 特点:与原系统等价;使用了Park和Moon的不等式 -2a图L日-waR+n -2aw=日w'ze0 85 2021年9月13日
85 2021年9月13日 - - t t h (III) Park & Moon : x(t) [A Ad ]x(t) Ad x(s)d s - - t t h y t A Ad x t Ad x s d s x t y t ( ) [ ] ( ) ( ) ( ) ( ) (IV) Fridman : 特点:与原系统等价;使用了Park和Moon的不等式 2 , ( ) ( ) 1 Z M R I R RM I b a M R Z R RM b a a b T T T T - - 2 , 0 - - - Y Z X Y b a Y N Z X Y N b a a Nb T T T T T 确定模型变换方法(3) 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中国地质大学自动化学院吴敏 确定模型变换方法(4) 局限性:本质上都是用x0)-(s)d替换x。 例如,在Moon(JC,2001)中,对于下式(t)中的x(-)前面被替换,而后面的 没有替换。 (x,)=2xT()P()+…+h(t)Z()+… =2x()PLx())+Aax(t-h]+…+hT()Z()+… =200+40-,sb+ 相当于:2@P0-〔e达--=0加入到) 86 2021年9月13日
86 2021年9月13日 局限性:本质上都是用 - - 替换x(t-h) 。 t t h x(t) x(s)ds - - - t t h d d T T d T T T t x t P Ax t A x t A x s d s x t P Ax t A x t h hx t Zx t V x x t Px t hx t Zx t 2 ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) ( ) x (t) 确定模型变换方法(4) 例如,在Moon (IJC, 2001)中,对于下式 中的x(t-h)前面被替换,而后面的 没有替换。 2 ( ) ( ) ( ) ( ) 0 ( )t t t h d T x t PA x t x s ds x t h V x - - - - 相当于: 加入到 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 参数化模型变换 (t)=Ax(t)+Adx(t-h) Q ()=Ax(t)+(Ad-C)x(t-h)+Cx(t-h) 特点:将时滞项分成两部分,一部分看成时滞无关部分,另一部分用确定的 模型变换来处理。 局限性: ·C是一个待定的固定参数,对矩阵A的没有有效的分解方法 ·需要结合确定模型变换,仍然具有其局限性 2x'0PC[0)-sds-t-0]=0 87 2021年9月13日
87 2021年9月13日 x(t) Ax(t) A x(t h) d - x(t) Ax(t) (A C)x(t h) Cx(t h) d - - - 局限性: C是一个待定的固定参数,对矩阵Ad的没有有效的分解方法 需要结合确定模型变换,仍然具有其局限性 特点:将时滞项分成两部分,一部分看成时滞无关部分,另一部分用确定的 模型变换来处理。 2 ( ) ( ) ( ) ( ) 0 - - - - x t PC x t x s ds x t h t t h T 参数化模型变换 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中固枕质大学自动化学院吴敏 自由权矩阵的引入 2x (P()-ds-)- 20Pc0-od-t--0 0 fsioN+xu-mw[-x-m-f]-0 注:将上式加入到Lyapunov泛函的导数中,保留所有的x(t-)项。由于N,和N,可 利用LMⅡ求解,与替换x(t-)项的固定权距阵方法相比,具有更大的优越性。 88 2021年9月13日
88 2021年9月13日 ( ) 1 ( ) 2 ( ) ( ) ( ) 0 - - - - - t t h T T x t N x t h N x t x t h x s d s 注:将上式加入到Lyapunov泛函的导数中,保留所有的x(t-h)项。由于N1和N2可 利用LMI求解,与替换x(t-h)项的固定权距阵方法相比,具有更大的优越性。 自由权矩阵的引入 2 ( ) ( ) ( ) ( ) 0 2 ( ) ( ) ( ) ( ) 0 - - - - - - - - x t PC x t x s ds x t h x t PA x t x s ds x t h t t h T t t h d T 先进控制理论与控制工程 吴 敏