
过程拉制原狸与爱用栽术 中周她质大学(武议)安剑奇 第5章被控过程特性及其数学模型 5.1被控过程的特性 5.2被控过程的数学模型 5.3解析法建立过程的数学模型 5.4实验辨识法建立过程的数学模型 5.5本章小结 3
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 5.2 被控过程的数学模型 5.3 解析法建立过程的数学模型 5.4 实验辨识法建立过程的数学模型 5.5 本章小结 第5章 被控过程特性及其数学模型 3

过程拉制原狸与爱用栽术 中周她质大学(武议)安剑奇 5.1被控过程的特性 ▣只有了解和掌握被控过程动态特性才能合理设计控制方案 ▣被控过程一般可划分为自衡特性与无自衡特性,单容特性 与多容特性,振荡与非振荡特性等 ▣以被控过程阶跃响应将典型的工业过程动态特性分为4类: ·自衡的非振荡过程 ,无自衡的非振荡过程 ·自衡的振荡过程 ·具有反向特性的过程 4
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 4 只有了解和掌握被控过程动态特性才能合理设计控制方案 被控过程一般可划分为自衡特性与无自衡特性,单容特性 与多容特性,振荡与非振荡特性等 以被控过程阶跃响应将典型的工业过程动态特性分为4类: • 自衡的非振荡过程 • 无自衡的非振荡过程 • 自衡的振荡过程 • 具有反向特性的过程

过程拉制原狸与爱用栽术 中图她质大学(武议)安剑奇 5.1被控过程的特性 > 自衡的非振荡过程 在原平衡状态出现干扰时,无需外加任何控制作用,被控过程能够自 发地趋于新的平衡状态 当进料等于出料时,过程处于平衡状态 增大进料阀开度,进料量发生阶跃响应,进 料量大于出料量,液位上升 液位上升导致出料阀静压增大,出料增加, 使液位上升速度减慢 最终进料等于出料,液位趋于新的平衡 具有自衡特性的液位过程
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 5 当进料等于出料时,过程处于平衡状态 增大进料阀开度,进料量发生阶跃响应,进 料量大于出料量,液位上升 液位上升导致出料阀静压增大,出料增加, 使液位上升速度减慢 最终进料等于出料,液位趋于新的平衡 自衡的非振荡过程 具有自衡特性的液位过程 在原平衡状态出现干扰时,无需外加任何控制作用,被控过程能够自 发地趋于新的平衡状态
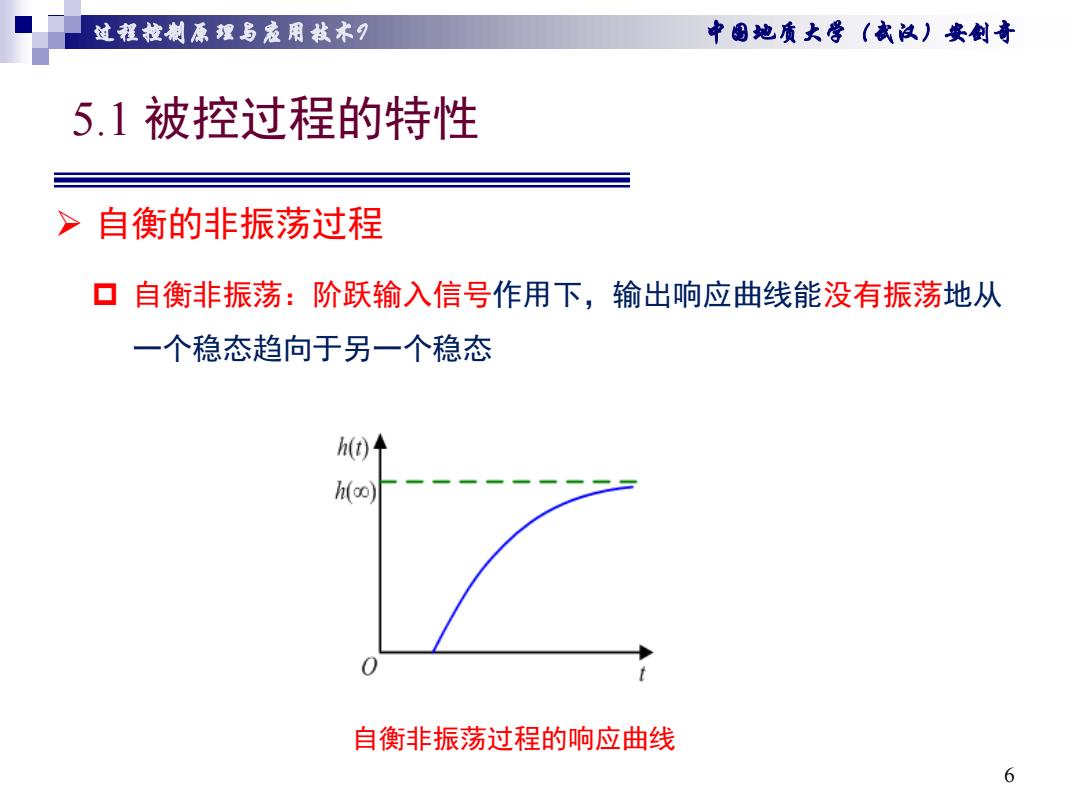
过程拉制原狸与爱用栽术 中围她质大学(武汉)安剑奇 5.1被控过程的特性 >自衡的非振荡过程 口自衡衡非振荡:阶跃输入信号作用下,输出响应曲线能没有振荡地从 一个稳态趋向于另一个稳态 h0↑ h(o) 自衡非振荡过程的响应曲线 6
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 6 自衡非振荡:阶跃输入信号作用下,输出响应曲线能没有振荡地从 一个稳态趋向于另一个稳态 自衡的非振荡过程 自衡非振荡过程的响应曲线
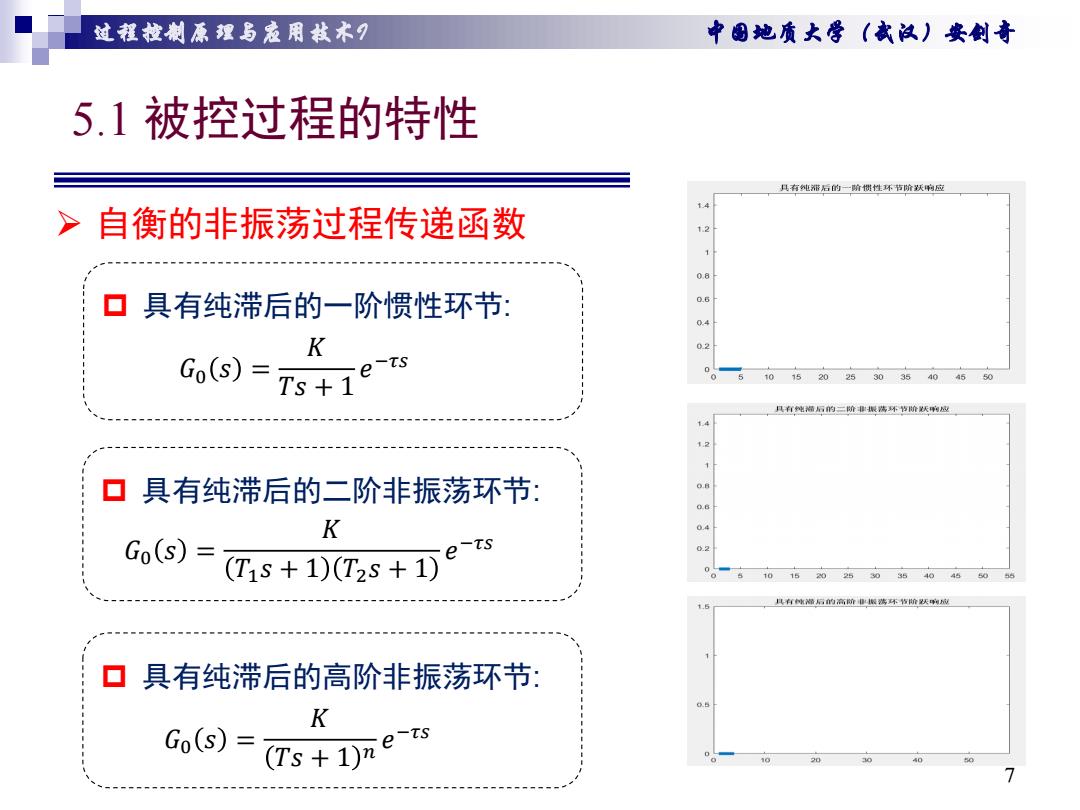
过程拉制原狸与爱用栽术月 中图她质大常(武议)安剑奇 5.1被控过程的特性 具有纯带后的一一阶惯性环节阶跃响应 >自衡的非振荡过程传递函数 1 0.8 】具有纯滞后的一阶惯性环节: 0.6 K as Go(s)= e-ts Ts+1 15 30 39 40 具有纯桶后的二阶律振落环节阶天胸应 12 具有纯滞后的二阶非振荡环节: K 04 Go(s)= e -ts 0.2 (T1S+1)(T2S+1) 具有纯滞后的高阶非振荡环节: K Go(s)= (Ts +1)n e-ts
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 7 具有纯滞后的一阶惯性环节: 自衡的非振荡过程传递函数 𝐺0 𝑠 = 𝐾 𝑇𝑠 + 1 𝑒 −𝜏𝑠 具有纯滞后的二阶非振荡环节: 具有纯滞后的高阶非振荡环节: 𝐺0 𝑠 = 𝐾 𝑇1𝑠 + 1 𝑇2𝑠 + 1 𝑒 −𝜏𝑠 𝐺0 𝑠 = 𝐾 𝑇𝑠 + 1 𝑛 𝑒 −𝜏𝑠
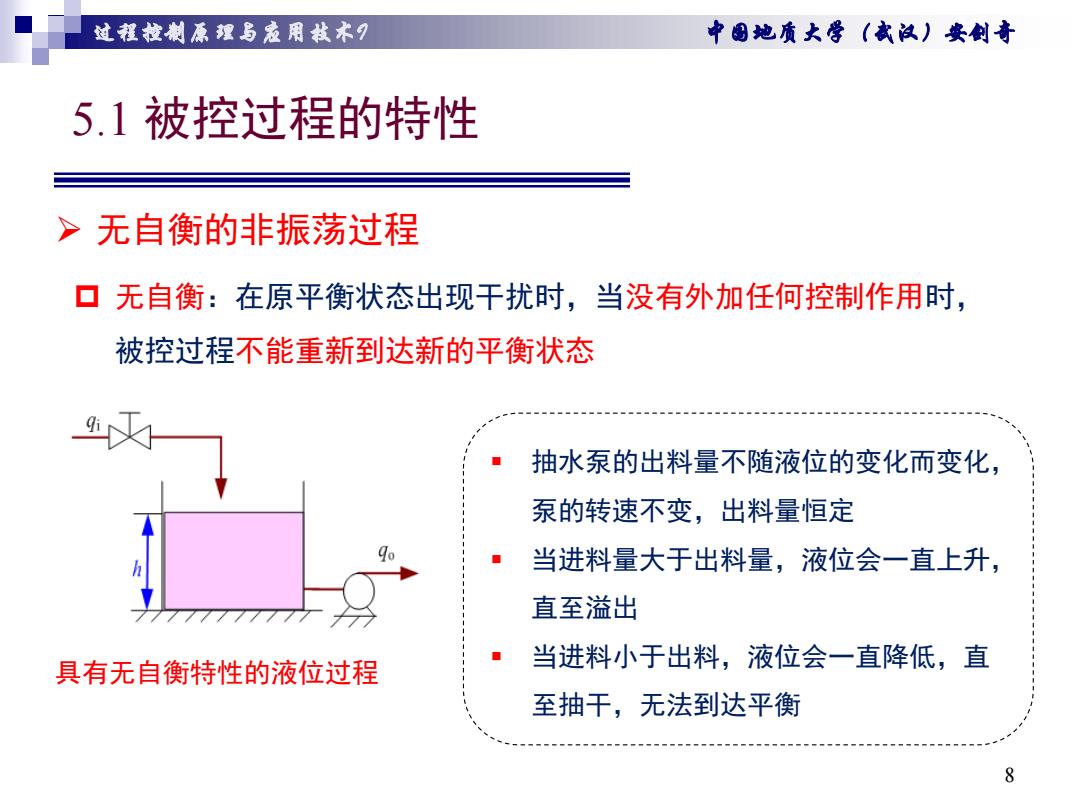
过程拉制原狸与爱用栽术月 中图她质大学(武议)安剑奇 5.1被控过程的特性 >无自衡的非振荡过程 口无自衡:在原平衡状态出现干扰时, 当没有外加任何控制作用时, 被控过程不能重新到达新的平衡状态 抽水泵的出料量不随液位的变化而变化, 泵的转速不变,出料量恒定 当进料量大于出料量,液位会一直上升, 直至溢出 具有无自衡特性的液位过程 当进料小于出料,液位会一直降低,直 至抽干,无法到达平衡 8
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 8 抽水泵的出料量不随液位的变化而变化, 泵的转速不变,出料量恒定 当进料量大于出料量,液位会一直上升, 直至溢出 当进料小于出料,液位会一直降低,直 至抽干,无法到达平衡 无自衡的非振荡过程 具有无自衡特性的液位过程 无自衡:在原平衡状态出现干扰时,当没有外加任何控制作用时, 被控过程不能重新到达新的平衡状态

过程拉制原狸与爱用栽术? 中图她质大学(武议)安剑奇 5.1被控过程的特性 >无自衡的非振荡过程 ▣无自衡非振荡:阶跃输入信号作用下,输出响应曲线会没有振荡 地从一个稳态一直上升或下降,不能达到新的稳态 h) 无自衡非振荡过程的响应曲线 9
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 9 无自衡非振荡:阶跃输入信号作用下,输出响应曲线会没有振荡 地从一个稳态一直上升或下降,不能达到新的稳态 无自衡的非振荡过程 无自衡非振荡过程的响应曲线

过程拉制原狸与爱用栽术 中图她质大学(武议)安剑奇 5.1被控过程的特性 具有浴后的一价织分环节阶利品 >无自衡的非振荡过程 ▣具有纯带后的一阶积分环节: 1 G(s)= ▣ 具有纯带后的二阶非振荡环节: K Go(s)= T1s(T2S+1) e-ts 02 0.3 0.4 0.50.60.7080.9 具有纯后的高阶非振环节阶天 36 30 ▣ 具有纯带后的高阶非振荡环节: 2 K Go(s)= Tis(Ts+1)n-ie-ts 10 10
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 10 具有纯滞后的一阶积分环节: 无自衡的非振荡过程 𝐺0 𝑠 = 1 𝑇𝑠 𝑒 −𝜏𝑠 具有纯滞后的二阶非振荡环节: 具有纯滞后的高阶非振荡环节: 𝐺0 𝑠 = 𝐾 𝑇1𝑠 𝑇2𝑠 + 1 𝑒 −𝜏𝑠 𝐺0 𝑠 = 𝐾 𝑇1𝑠 𝑇𝑠 + 1 𝑛−1 𝑒 −𝜏𝑠
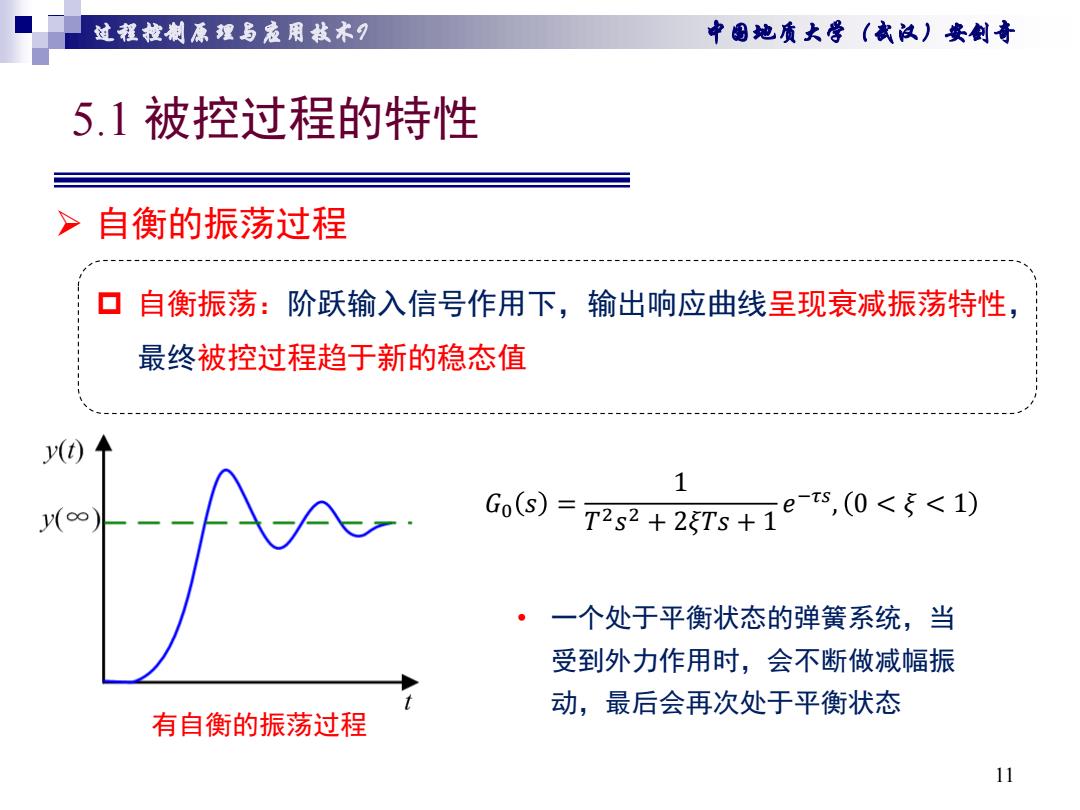
过程拉制原狸与爱用栽术月 中围她质大学(武汉)安剑奇 5.1被控过程的特性 > 自衡的振荡过程 自衡振荡:阶跃输入信号作用下,输出响应曲线呈现衰减振荡特性, 最终被控过程趋于新的稳态值 y() y(∞ G(s)= 2s2+25Ts+1e,(0<5<1) 一个处于平衡状态的弹簧系统,当 受到外力作用时,会不断做减幅振 动,最后会再次处于平衡状态 有自衡的振荡过程 11
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 11 自衡振荡:阶跃输入信号作用下,输出响应曲线呈现衰减振荡特性, 最终被控过程趋于新的稳态值 自衡的振荡过程 有自衡的振荡过程 𝐺0 𝑠 = 1 𝑇 2𝑠 2 + 2𝜉𝑇𝑠 + 1 𝑒 −𝜏𝑠 , 0 < 𝜉 < 1 • 一个处于平衡状态的弹簧系统,当 受到外力作用时,会不断做减幅振 动,最后会再次处于平衡状态
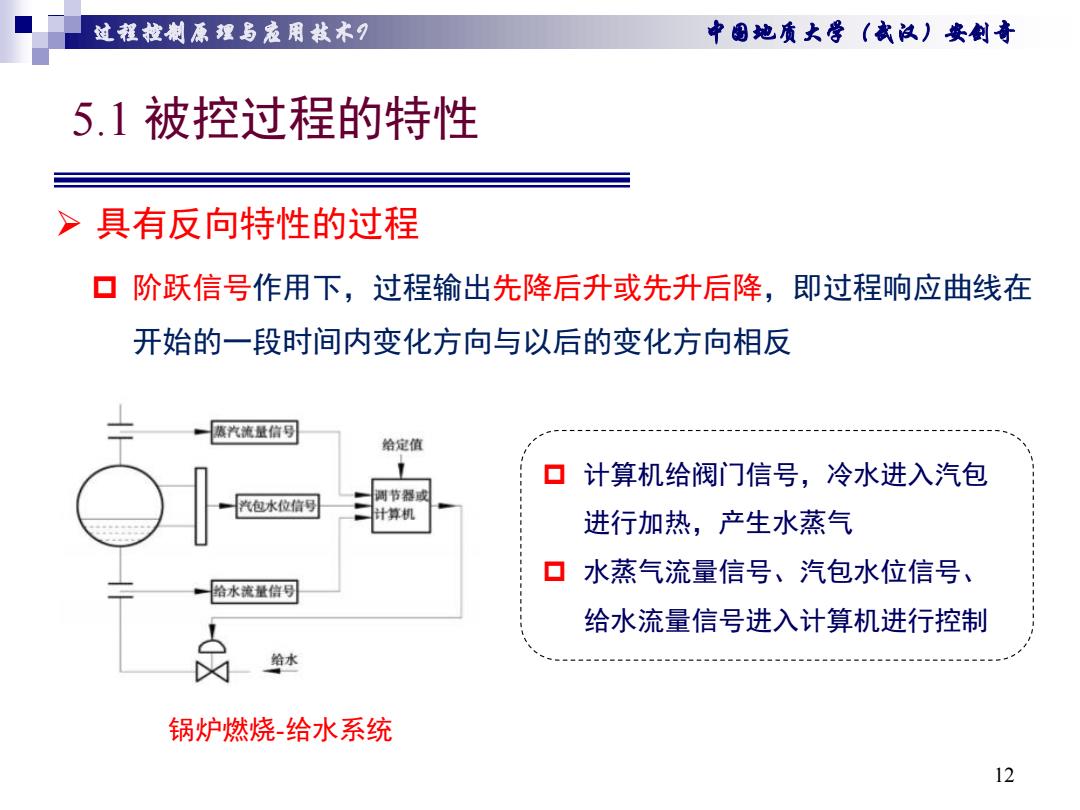
过程拉制原狸与爱用栽术月 中图她质大学(武议)安剑奇 5.1被控过程的特性 > 具有反向特性的过程 ▣阶跃信号作用下,过程输出先降后升或先升后降,即过程响应曲线在 开始的一段时间内变化方向与以后的变化方向相反 ,汽流量信号 给定值 ▣ 计算机给阀门信号,冷水进入汽包 调节器或 汽包水位信号 计算机 进行加热,产生水蒸气 ▣ 水蒸气流量信号、汽包水位信号、 给水流量信习 给水流量信号进入计算机进行控制 给水 锅炉燃烧给水系统 12
过程控制原理与应用技术I 中国地质大学(武汉)安剑奇 5.1 被控过程的特性 12 阶跃信号作用下,过程输出先降后升或先升后降,即过程响应曲线在 开始的一段时间内变化方向与以后的变化方向相反 具有反向特性的过程 锅炉燃烧-给水系统 计算机给阀门信号,冷水进入汽包 进行加热,产生水蒸气 水蒸气流量信号、汽包水位信号、 给水流量信号进入计算机进行控制