
第二章过程特性 华东理工大学信息学院自动化系
第二章 过程特性 华东理工大学信息学院自动化系
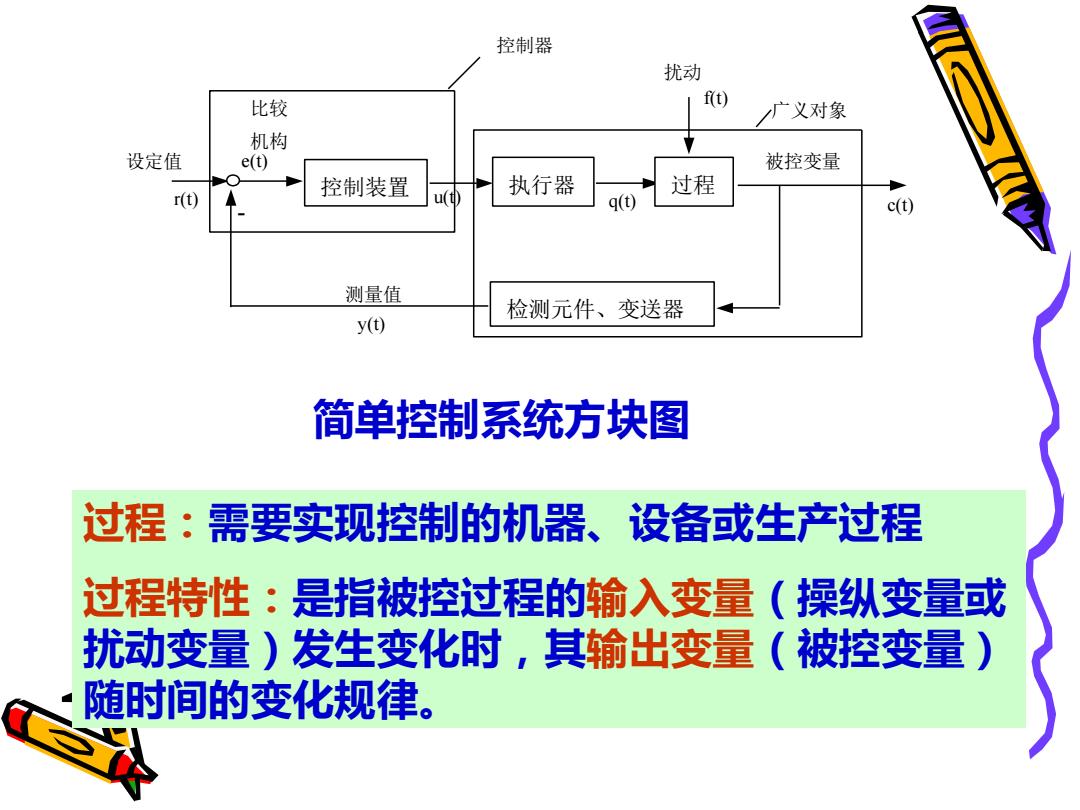
控制器 S 扰动 比较 f(t) 广义对象 机构 设定值 e(t) 被控变量 ●) 控制装置 执行器 过程 r(t) u(t) q(t) c(t) 测量值 检测元件、变送器 y() 简单控制系统方块图 过程:需要实现控制的机器、 设备或生产过程 过程特性:是指被控过程的输入变量(操纵变量或 扰动变量)发生变化时,其输出变量(被控变量) 随时间的变化规律
控制装置 执行器 过程 检测元件、变送器 r(t) 比较 机构 - e(t) u(t) q(t) y(t) f(t) c(t) 扰动 广义对象 被控变量 测量值 控制器 设定值 过程:需要实现控制的机器、设备或生产过程 过程特性:是指被控过程的输入变量(操纵变量或 扰动变量)发生变化时,其输出变量(被控变量) 随时间的变化规律。 简单控制系统方块图

研究过程特性的必要性: 为了更好地实施控制
研究过程特性的必要性: 为了更好地实施控制

本章研究内容: 2.1过程特性的类型 2.2过程的数学描述 2.3过程特性的一般分析 2.4过程特性的实验测定方法 最
本章研究内容: 2.1 过程特性的类型 2.2 过程的数学描述 2.3 过程特性的一般分析 2.4 过程特性的实验测定方法

2.1过程特性的类型 通道:输入变量对输出变量的作用途径 控制通道 :操纵变量q()对被控变量c()的作用途径 扰动通道:扰动变量)对被控变量c()的作用途径 广义对象特性主要通过响应曲线来呈现 控制通道的响应曲线:当被控作用()做阶跃变化 (扰动)不变)时被控变量的时间特性c(@ 扰动通道的响应曲线:当扰动)做阶跃变化(控制 作用u(①不变)时被控变量的时间特性c()
2.1 过程特性的类型 广义对象特性主要通过响应曲线来呈现 通道: 扰动通道: 控制通道: 输入变量对输出变量的作用途径 操纵变量q(t)对被控变量c(t)的作用途径 扰动变量f(t)对被控变量c(t)的作用途径 控制通道的响应曲线:当被控作用u(t)做阶跃变化 (扰动f(t)不变)时被控变量的时间特性c(t) 扰动通道的响应曲线:当扰动f(t)做阶跃变化(控制 作用u(t) 不变)时被控变量的时间特性c(t)
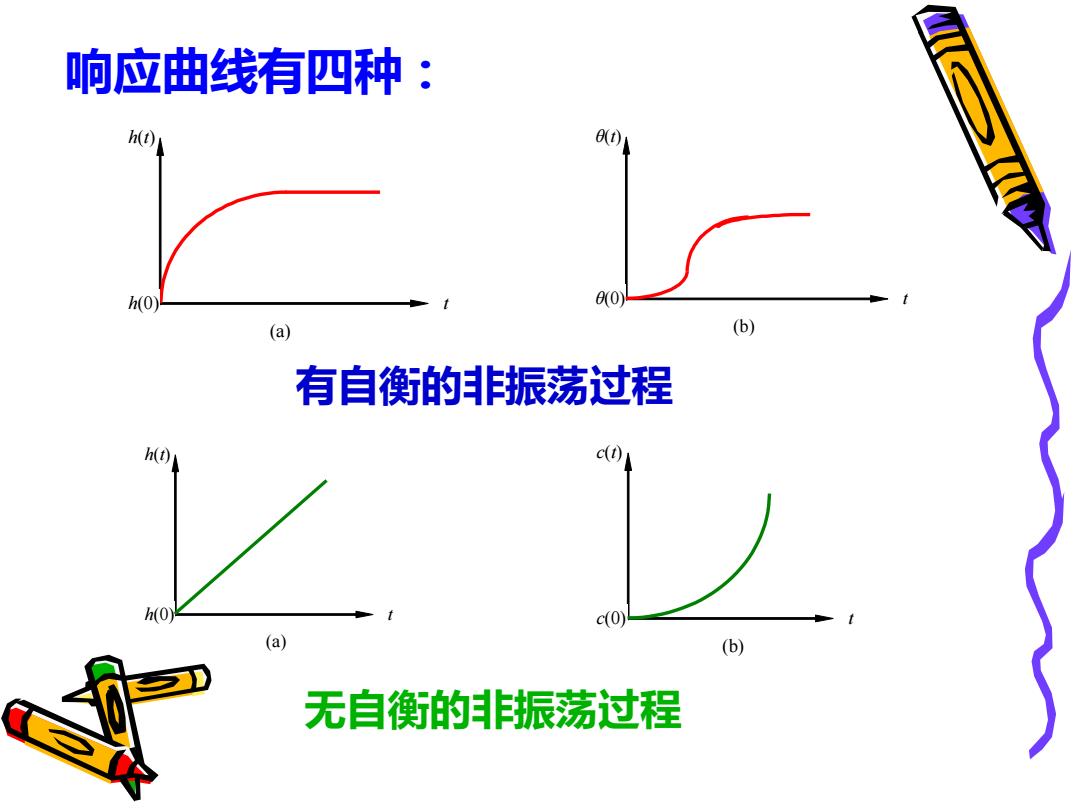
响应曲线有四种: h(t) θt) h(0 00) (a) (b) 有自衡的非振荡过程 h(t) c(0) (a) (b) 无自衡的非振荡过程
响应曲线有四种: h(t) h(0) t (a) θ(t) θ(0) t (b) 有自衡的非振荡过程 h(t) h(0) t (a) c(t) c(0) t (b) 无自衡的非振荡过程

c(1) c() c(0 c(0) 有自衡的振荡过程 具有反向特性的过程
c(t) c(0) t c(t) c(0) t 有自衡的振荡过程 具有反向特性的过程
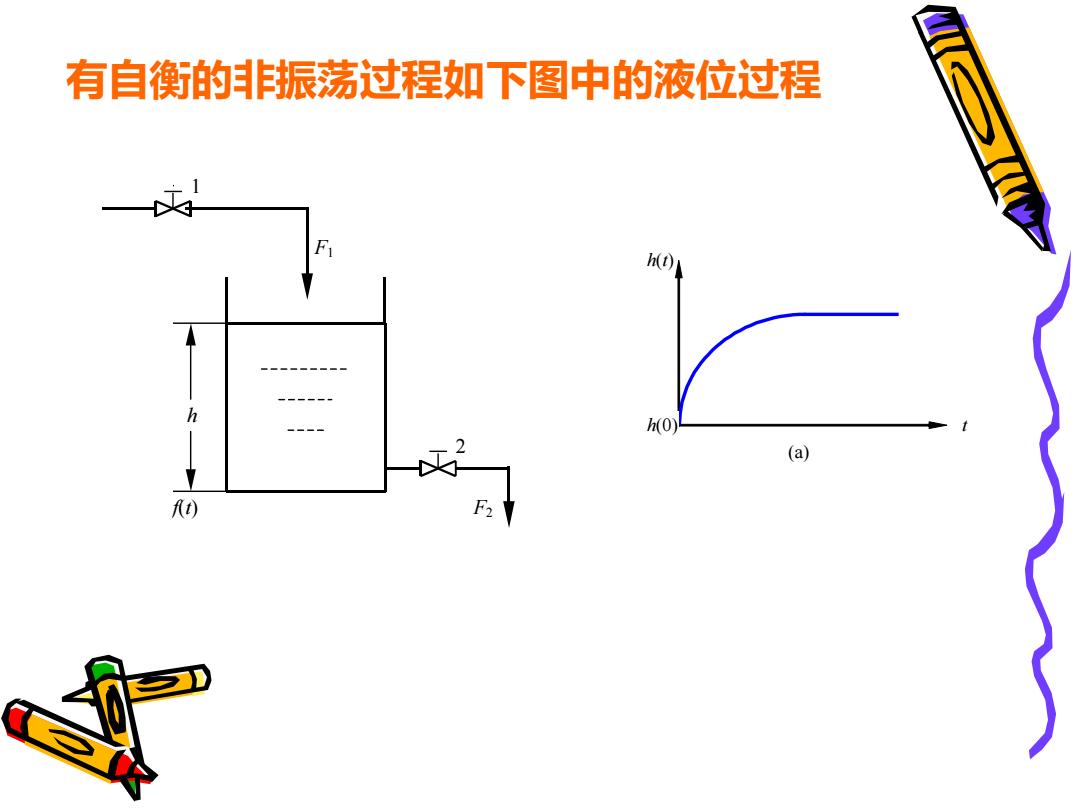
有自衡的非振荡过程如下图中的液位过程 F h(t) h h0) (a) F2
f(t) 1 F1 F2 2 h 有自衡的非振荡过程如下图中的液位过程 h(t) h(0) t (a)
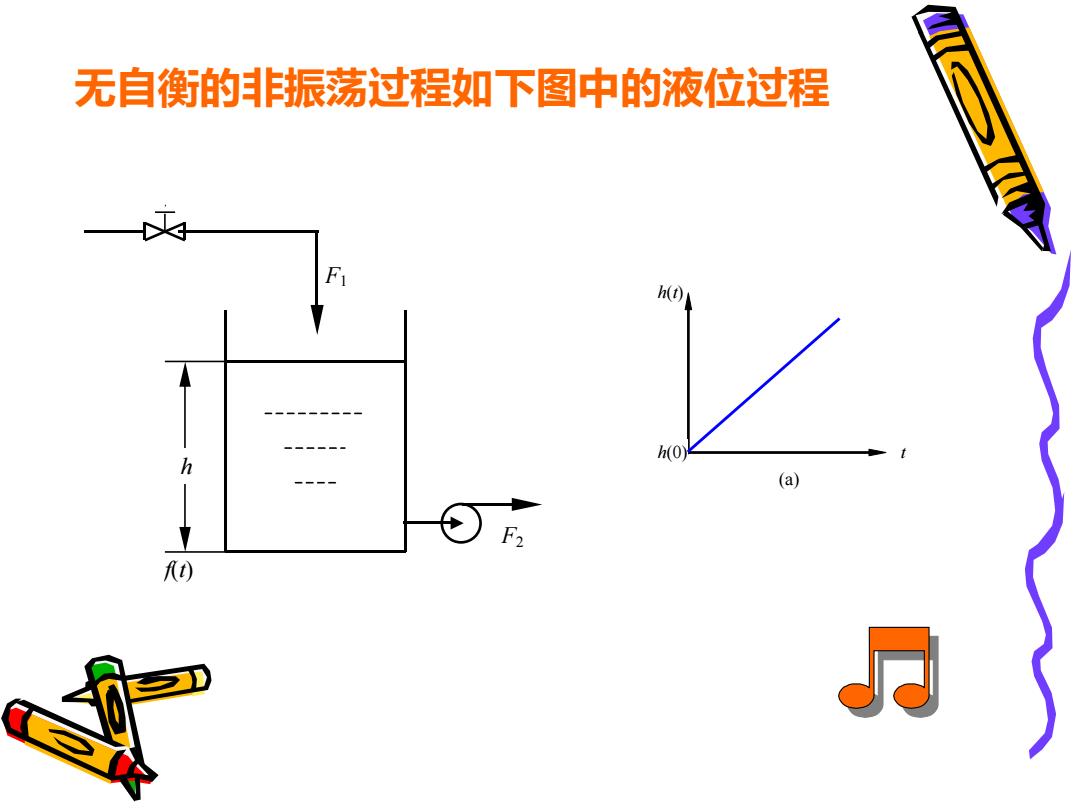
无自衡的非振荡过程如下图中的液位过程 h(t) h(0 (a) F2 同
f(t) F1 F2 h 无自衡的非振荡过程如下图中的液位过程 h(t) h(0) t (a)

2.2过程的数学描述 要研究被控过程的特性,就必须知道被控过程的 数学模型(参量模型),也就是对过程的数学描述。 数学模型:表示具体过程的输入、输出关系的数学方 程式。 其形式有:微分方程式、偏微分方程式、状态方程 热物料 蒸汽加 蒸汽 热器 冷物料
2.2 过程的数学描述 要研究被控过程的特性,就必须知道被控过程的 数学模型(参量模型),也就是对过程的数学描述。 数学模型:表示具体过程的输入、输出关系的数学方 程式。 其形式有:微分方程式、偏微分方程式、状态方程 热物料 冷物料 蒸汽 蒸汽加 热器