
5.8S域分析、极点与 零点 决定系统的时域响应 决定系统频率响应 决定系统稳定性 1
1 5.8 S域分析、极点与 零点 决定系统的时域响应 决定系统频率响应 决定系统稳定性

系统函数的定义 ·系统零状态下,响应的拉氏变换与激励 拉氏变换之比叫作系统函数,记作H(s). H(S)= R(s) E(s) 。1 可以是电压传输比、电流传输比、转移 阻抗、转移导纳、策动点阻抗或导纳 2
2 系统函数的定义 • 系统零状态下,响应的拉氏变换与激励 拉氏变换之比叫作系统函数,记作H(s). • 可以是电压传输比、电流传输比、转移 阻抗、转移导纳、策动点阻抗或导纳 ( ) ( ) ( ) E s R s H s
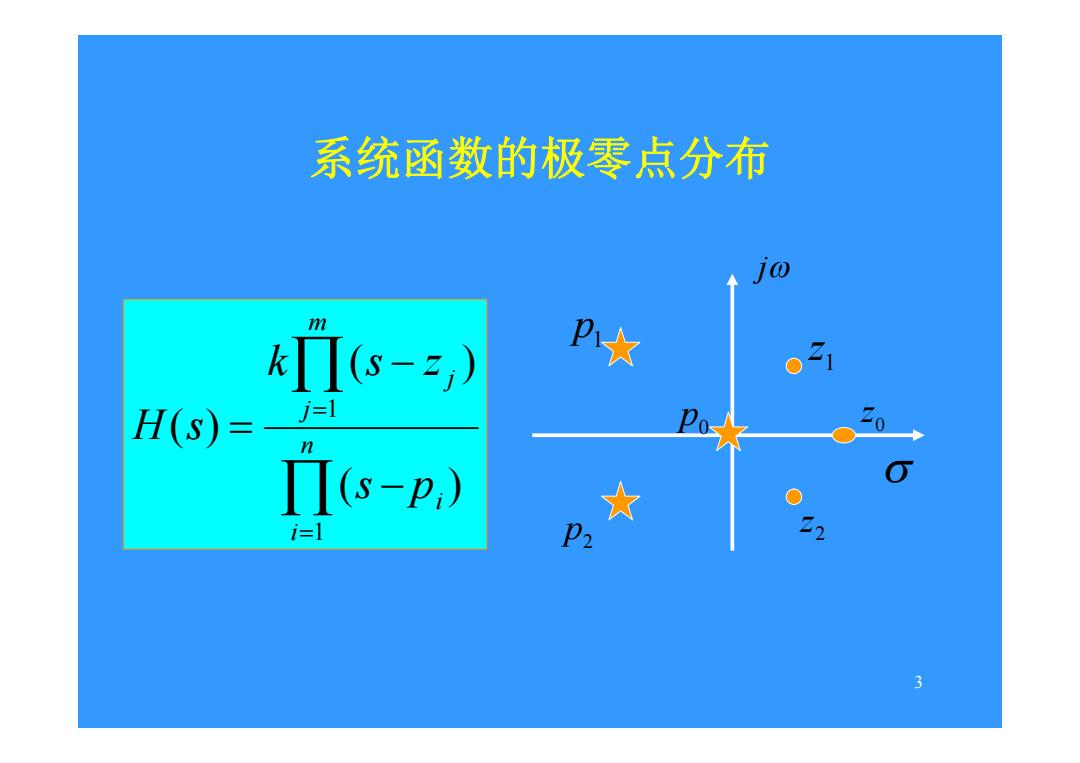
系统函数的极零点分布 m Πs-,) H(s)== n Πs-p,)》 大 i=l P2 3
3 系统函数的极零点分布 n i i m j j s p k s z H s 1 1 ( ) ( ) ( ) j 0 z 1 z 2 z p0 p1 p2
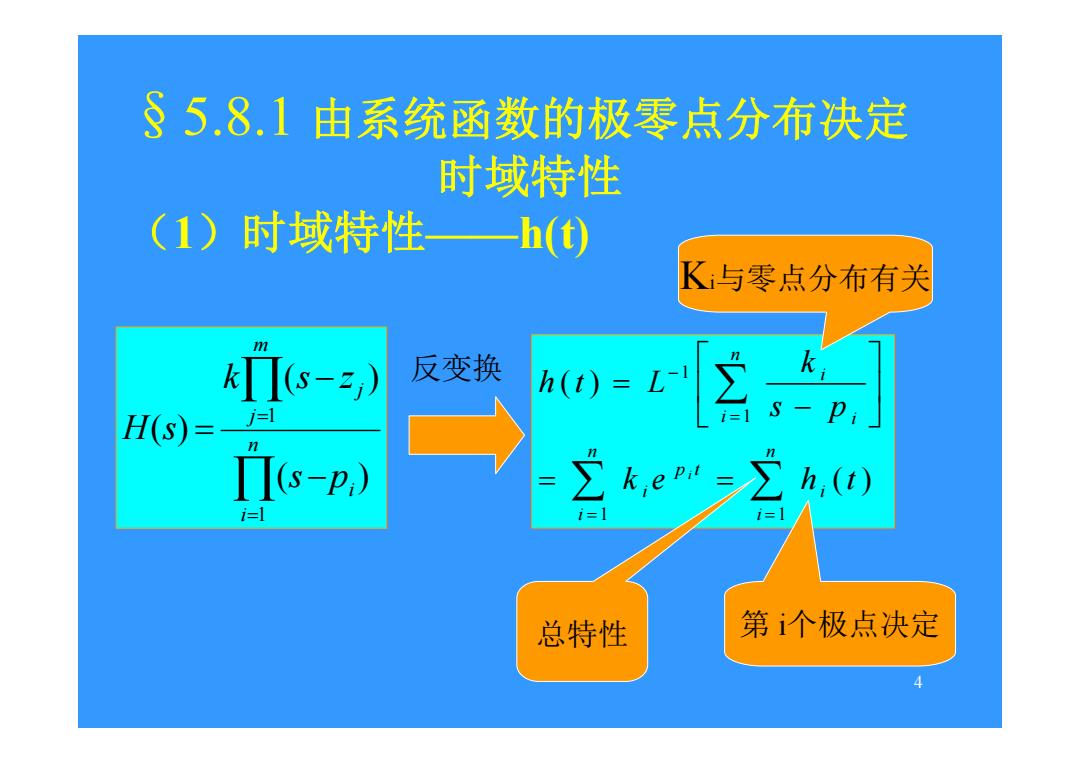
§5.8.1由系统函数的极零点分布决定 时域特性 (1)时域特性一h(t) K与零点分布有关 m kΠs-)》 反变换 l H(s)= 2 Πs-p,) ∑k,e二h,() i=1 i= i=1 总特性 第个极点决定 4
4 §5.8.1 由系统函数的极零点分布决定 时域特性 (1)时域特性——h(t) n i i m j j s p k s z H s 1 1 ( ) ( ) ( ) 反变换 n i i n i p t i n i i i k e h t s p k h t L i 1 1 1 1 ( ) ( ) 总特性 第 i个极点决定 Ki与零点分布有关
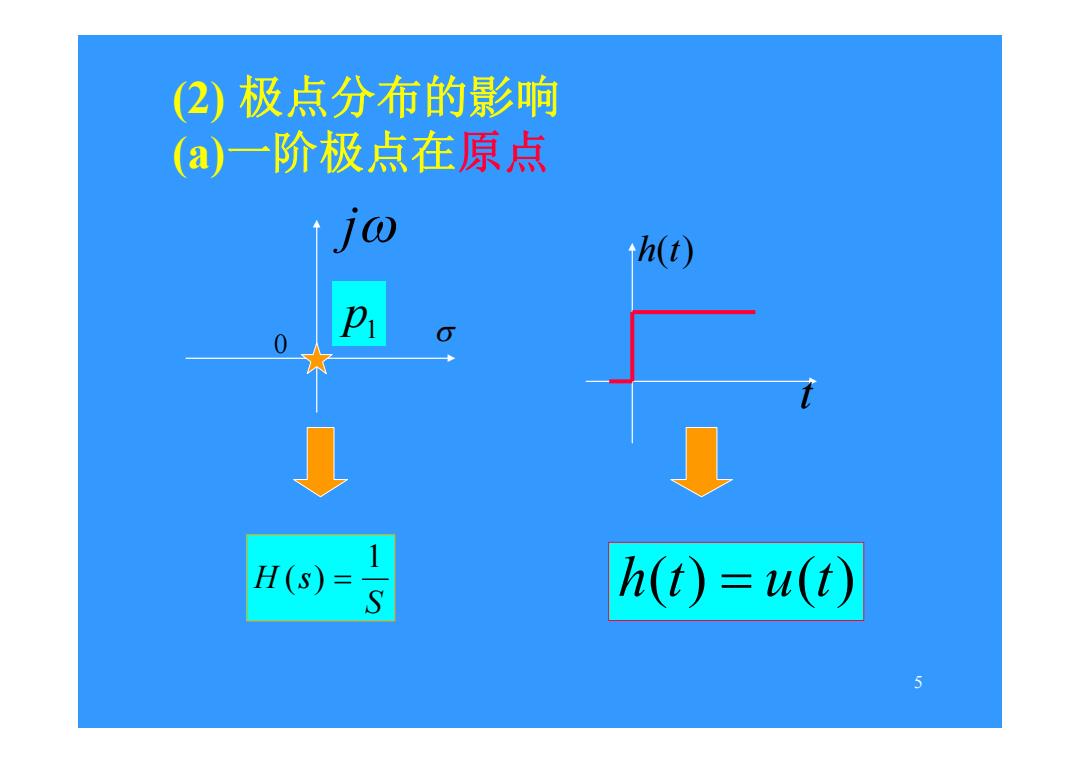
(2)极点分布的影响 (a)一阶极点在原点 h(t) 0 0 H(s) h(t)=u(t) 5
5 (2) 极点分布的影响 (a)一阶极点在原点 j 0 p1 S H s 1 ( ) t h(t) h(t) u(t)

(2)几种典型的极点分布 (b)一阶极点在负实轴 jo h(t) e -0 0 H(s)= S+a h(t)=e 6
6 (2) 几种典型的极点分布—— (b)一阶极点在负实轴 j 0 S H s 1 ( ) t h(t) t h t e ( ) t e 1 p
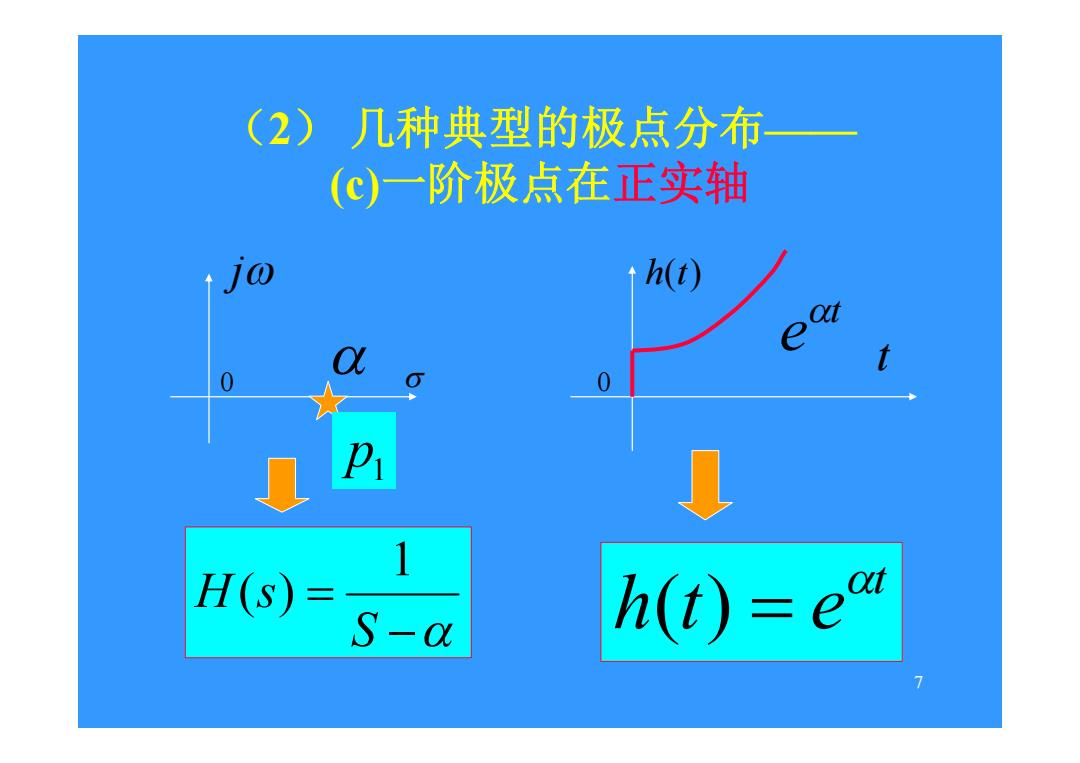
(2)几种典型的极点分布 (c)一阶极点在正实轴 h(t) e H(s)= S-a h(t)-ea 7
7 (2) 几种典型的极点分布—— (c)一阶极点在正实轴 j 0 S H s 1 ( ) h(t) t 0 t h t e ( ) t e p1

(2)几种典型的极点分布 (d)一阶共轭极点在虚轴上 /@ P1*j0 0 P2 *-j01 01 H(5)=+ h(t)=sino,t.u(t)》 8
8 (2) 几种典型的极点分布—— (d)一阶共轭极点在虚轴上 j 0 1 j 1 j 2 1 2 1 ( ) S H s ( ) sin . ( ) 1 h t t u t t h(t) 0 p1 p2

(2)几种典型的极点分布 (e)共轭极点在虚轴上,原点有一零点 0 P2 -j01 S H(s)=2+ h(t)=cos@tu(t) 9
9 j 0 1 j 1 j 2 1 2 ( ) S S H s (2) 几种典型的极点分布—— (e)共轭极点在虚轴上,原点有一零点 ( ) cos . ( ) 1 h t t u t t h(t) 0 1 p p2
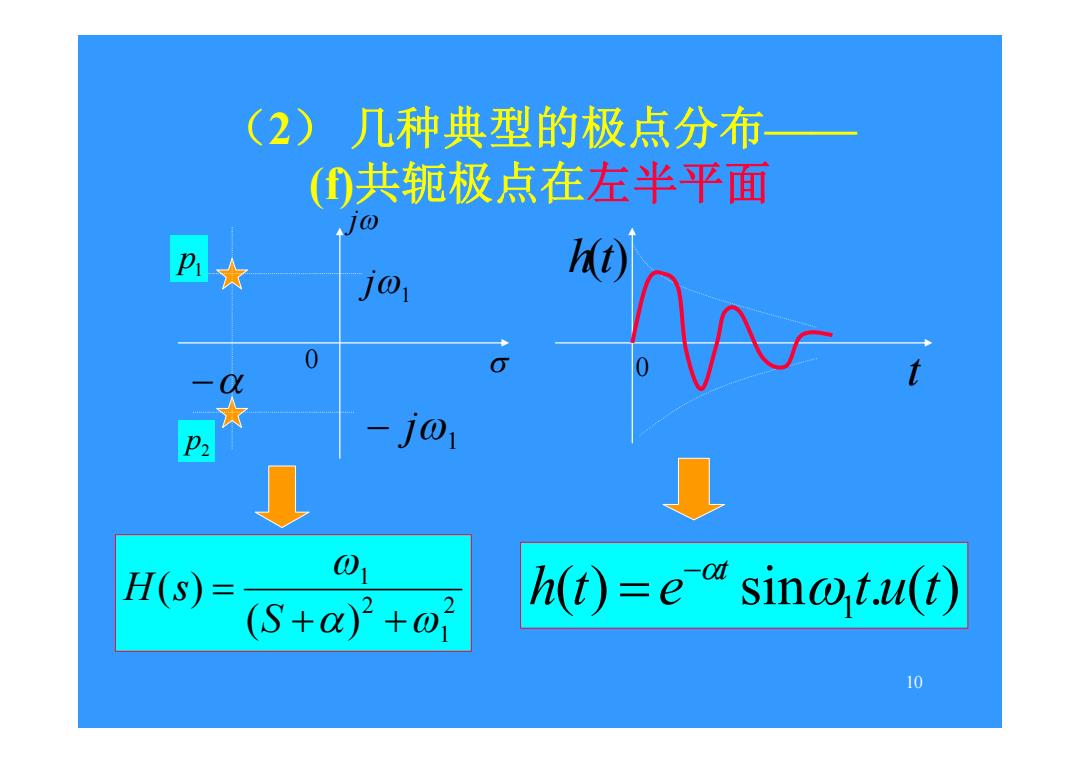
(2)几种典型的极点分布 ()共轭极点在左半平面 j01 0 P2 -j01 H(S)2 01 (S+)2+o1 h(t)=esinotu(t) 10
10 (2) 几种典型的极点分布—— (f)共轭极点在左半平面 j 0 1 j 1 j 2 1 2 1 ( ) ( ) S H s ( ) sin . ( ) 1 h t e t u t t t h(t) 0 2 p p1