
§1-1-4信号的分解 ·直流分量和交流分量 •偶分量与奇分量 •脉冲分量 •实部分量与虚部分量 1
1 §1-1-4 信号的分解 •直流分量和交流分量 •偶分量与奇分量 •脉冲分量 •实部分量与虚部分量
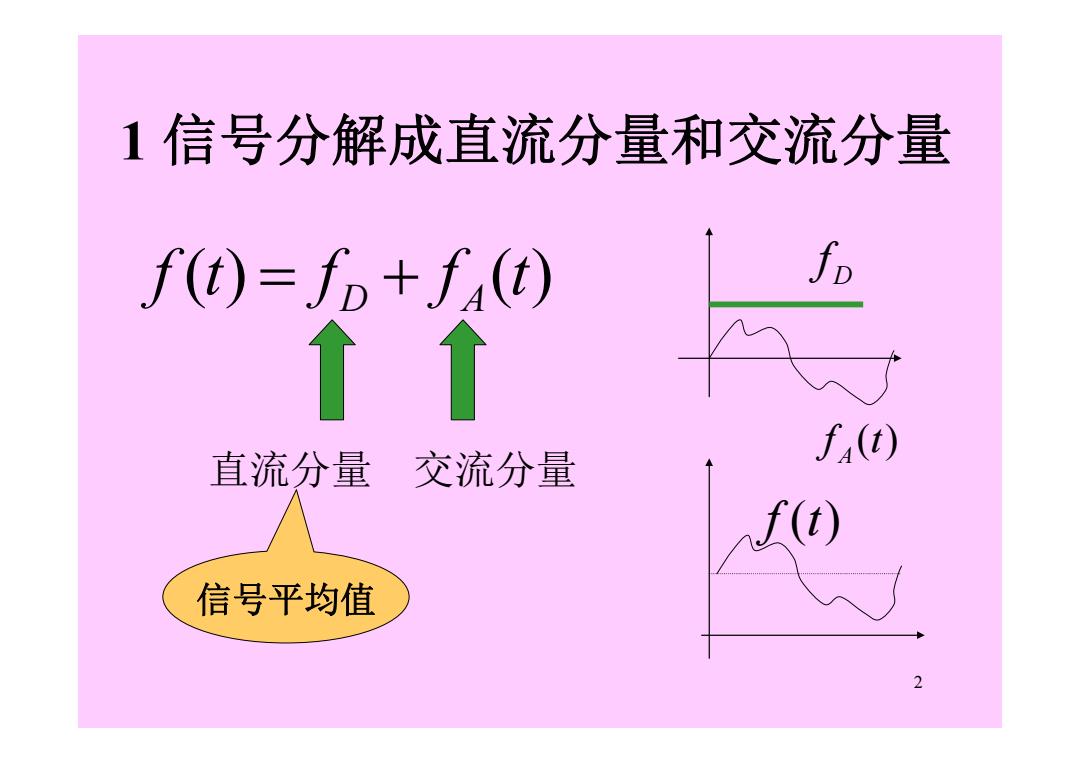
1信号分解成直流分量和交流分量 f()=f+t 直流分量 f(t) 交流分量 L() 信号平均值 2
2 1 信号分解成直流分量和交流分量 直流分量 交流分量 f (t) f f (t) D A D f f (t) A f (t) 信号平均值
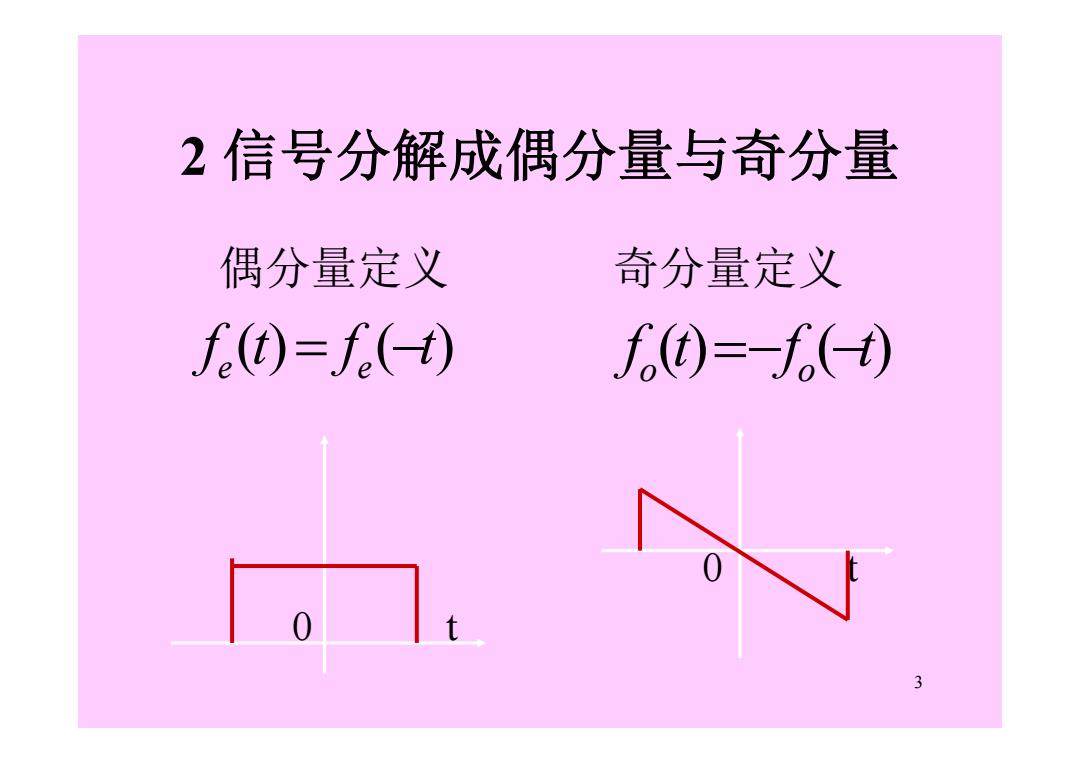
2信号分解成偶分量与奇分量 偶分量定义 奇分量定义 f(t)=f() f)=-f() 3
3 2 信号分解成偶分量与奇分量 偶分量定义 奇分量定义 0 t 0 t f (t) f ( t) e e f (t) f ( t) o o

信号分解为奇、偶分量: 偶分量:f(t)=f(-) 奇分量:6(t)=-(-t) 信号 f(t)可表示为: f(t)=[f(t)+f(t)+f(-t)-f(-t)] =[f(t)+f(-t)]+[f(t)-f(-t)] =f(t)+f(t) 偶分量 .f(t)=[f(t)+f(-t)] f.(t) 奇分 f(t)=2[f(t)-f(-)] 量f,() 4
4 信号分解为奇、偶分量: ( ) ( ) ( ) ( ) 0 0 f t f t f t f t 偶分量:e e 奇分量: ( ) ( ) [ ( ) ( )] [ ( ) ( )] ( ) [ ( ) ( ) ( ) ( )] ( ) 0 2 1 2 1 2 1 f t f t f t f t f t f t f t f t f t f t f t f t e 信号 可 表示为: 偶分量 fe (t) 奇分 量fo (t) ( ) [ ( ) ( )] ( ) [ ( ) ( )] 2 1 0 2 1 f t f t f t f t f t f t e
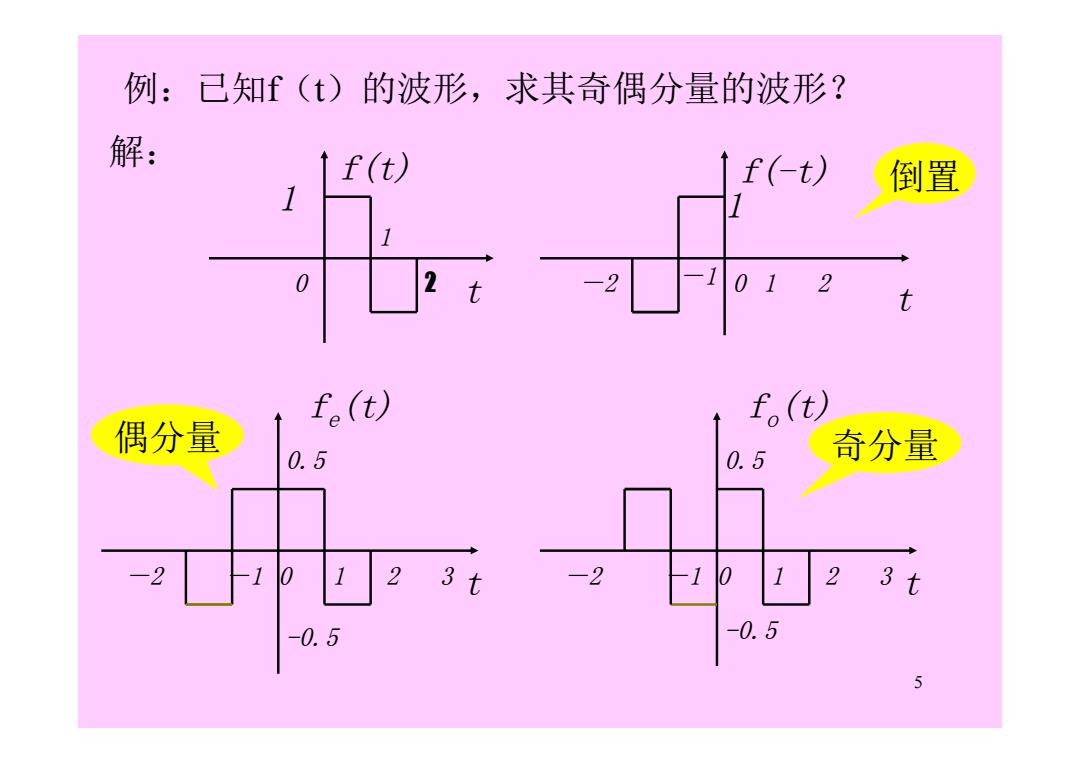
例:己知f(t)的波形,求其奇偶分量的波形? 解: f(t) f(-t) 倒置 1 1 0 01 2 t fe(t) f。(t) 偶分量 0.5 0.5 奇分量 -2 -10 123t -2 -1 0 23t -0.5 -0.5 5
5 例:已知f(t)的波形,求其奇偶分量的波形? 解: f(t) t 1 0 1 2 f(-t) t 0 1 1 - -1 2 2 倒置 fo(t) t 0 1 0.5 -2 -1 2 3 奇分量 -0.5 fe(t) t 0 1 0.5 -2 -1 2 3 偶分量 -0.5
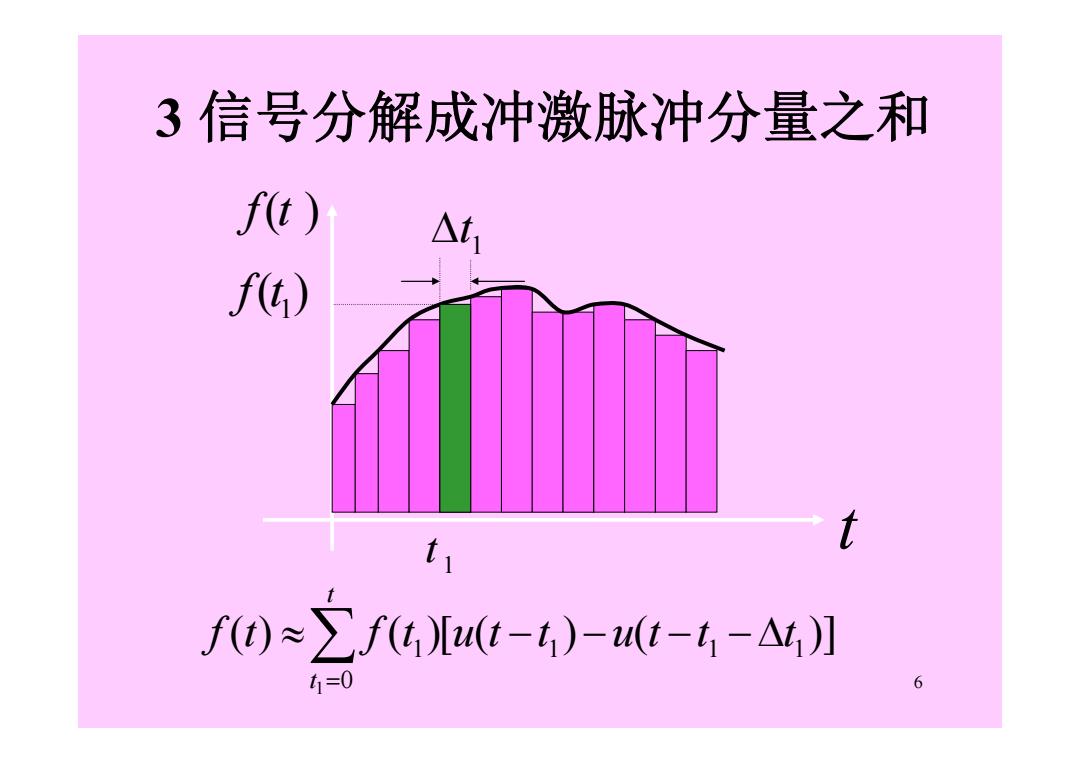
3信号分解成冲激脉冲分量之和 f() △t f) t t f0≈∑fGUt-4)-4t-4-4,】 t1=0 6
6 3 信号分解成冲激脉冲分量之和 ( ) ( )[ ( ) ( )] 1 1 1 0 1 1 f t f t u t t u t t t t t 1 t ( ) 1 f t 1 t t f(t )

f0≈∑fG4t-)-4t-4-4,】 t1=0 f0)=m2f0)4-)-w--】x 0 t1=0 4 f)=lim∑ft)δt-4)△1, △10 1=0 f)=f45u-4).d 变量置换: 积分变量t,→t,观察时刻t→t。 筛选特性 f6o)=f0δt-t)d 7
7 1 1 0 1 0 ( ) lim ( ) ( ). 1 1 f t f t t t t t t t 1 1 0 1 f (t) f (t ) (t t ).dt t 1 0 积分变量t t, 观察时刻t t 0 0 0 0 ( ) ( ) ( ) t f t f t t t dt 变量置换: 1 1 1 1 1 0 1 0 [ ( ) ( )] ( ) lim ( ) 1 1 t t u t t u t t t f t f t t t t 筛选特性 ( ) ( )[ ( ) ( )] 1 1 1 0 1 1 f t f t u t t u t t t t t

4分解成实部分量和虚部分量 ∫(t)=f,(t)+if,(t) (t)=f,(t)-f:(t) f,()=[f()+f(t)] jf()=Lf(t)-f()] 8
8 4 分解成实部分量和虚部分量 f (t ) f (t ) jf (t ) r i ( ) ( ) ( ) * f t f t jf t r i ( ) [ ( ) ( )] * 2 1 f t f t f t r ( ) [ ( ) ( )] * 2 1 j f t f t f t i