
Ch4 Ch4傅立什变换在系统分析中的应用 本章与第三章的关系 第三章傅立什变换侧重于信号的分析 本章侧重于系统分析,是第三章的延续。 Recall: f(t)*h(t)>F(iω)H(jω) f(t) y(t) h(t) F(jo) Y(jo) H(j@) 1
1 本章与第三章的关系: 第三章傅立叶变换侧重于信号的分析, 本章侧重于系统分析,是第三章的延续。 Recall: f (t)*h(t) F( j)H( j) h(t) f(t) y(t) H(j) F(j) Y(j) Ch4 傅立叶变换在系统分析中的应用

本章与拉氏变换的关系: Ch4 是拉氏变换的一个特例,专门趼究系统的 频域特性 Recall:对于稳定(临界)系统,由如下关系: FUjw)=F(s=o+∑K,zo-O,)》 k=1 本章面向的系统是严格稳定系统: H(j@)=H(s) 2
2 本章与拉氏变换的关系: • 是拉氏变换的一个特例,专门研究系统的 频域特性 • Recall:对于稳定(临界)系统,由如下关系: = = = + − n k s j Kn n F j F s 1 ( ) ( ) ( ) • 本章面向的系统是严格稳定系统: ( ) ( ) H j H s s j = =

Ch4 Ch4傅立十变换在系统分析中的应用 Application:滤波、调制、抽样 Contents: 系统的频率响应 H(jo)frequency response 无失真传输 理想低通滤波器 调制与解调 零阶保持抽样 ·多路复用 3
3 Ch4 傅立叶变换在系统分析中的应用 Application: 滤波、调制、抽样 • 系统的频率响应 H(j)frequency response • 无失真传输 • 理想低通滤波器 • 调制与解调 • 零阶保持抽样 • 多路复用 Contents:

1频率可响应 0h4 Frequency response H(jw) LT中的定义:正弦激动下的稳态响应。 For LTI system f(t),h(t), y(t) y(t)=f(t)*h(t) Y(jw)=F(jo)H(iω) Defl: H(j0)= Y(j@) =FT[h(t)] F(jo) 4
4 1 频率响应 Frequency response H(jw) For LTI system : f(t), h(t), y(t) y(t) = f (t)*h(t) Y( j) = F( j)H( j) [ ( )] ( ) ( ) ( ) FT h t F j Y j H j = = Def1: LT中的定义:正弦激励下的稳态响应

Def2:对稳定系统 Ch4 ·LCCDE: dky(t) m ∑b, d f(t) k=0 1=0 dt >∑a(iw)Y(jio)=∑b,(io)'F(io) k=0 1=0 Y(jω) b,(Jjo)Y H(j@)- 1=0 F(jω) 之ak(jo) 解方程: k=0 y(t)=FT[Y(jo)]=FT[F(jo)H(jo)] 5
5 • LCCDE: Def 2: 对稳定系统 l m l l k l n k k k dt d f t b dt d y t a ( ) ( ) 0 0 = = = = = = m l l l k n k k a j Y j b j F j 0 0 ( ) ( ) ( ) ( ) k n k k m l l l a j b j F j Y j H j ( ) ( ) ( ) ( ) ( ) 0 0 = = = = ( ) [ ( )] [ ( ) ( )] 1 1 y t FT Y j FT F j H j − − = = 解方程:

2天失真传输 h4 在实际应用中对失真问题的研究有两类 (1)信号传输失真尽可能小 (2)有意识地产生失真(预失真波形的产生) 信号传输过程中引起失真的原因 (1)非线性失真(产生新的频率 (2)线性失真(不产生新的频率成分) 幅度失真 相位失真 6
6 2 无失真传输 • 在实际应用中对失真问题的研究有两类: (1)信号传输失真尽可能小 (2)有意识地产生失真(预失真波形的产生) • 信号传输过程中引起失真的原因: (1)非线性失真(产生新的频率) (2)线性失真(不产生新的频率成分) 幅度失真 相位失真
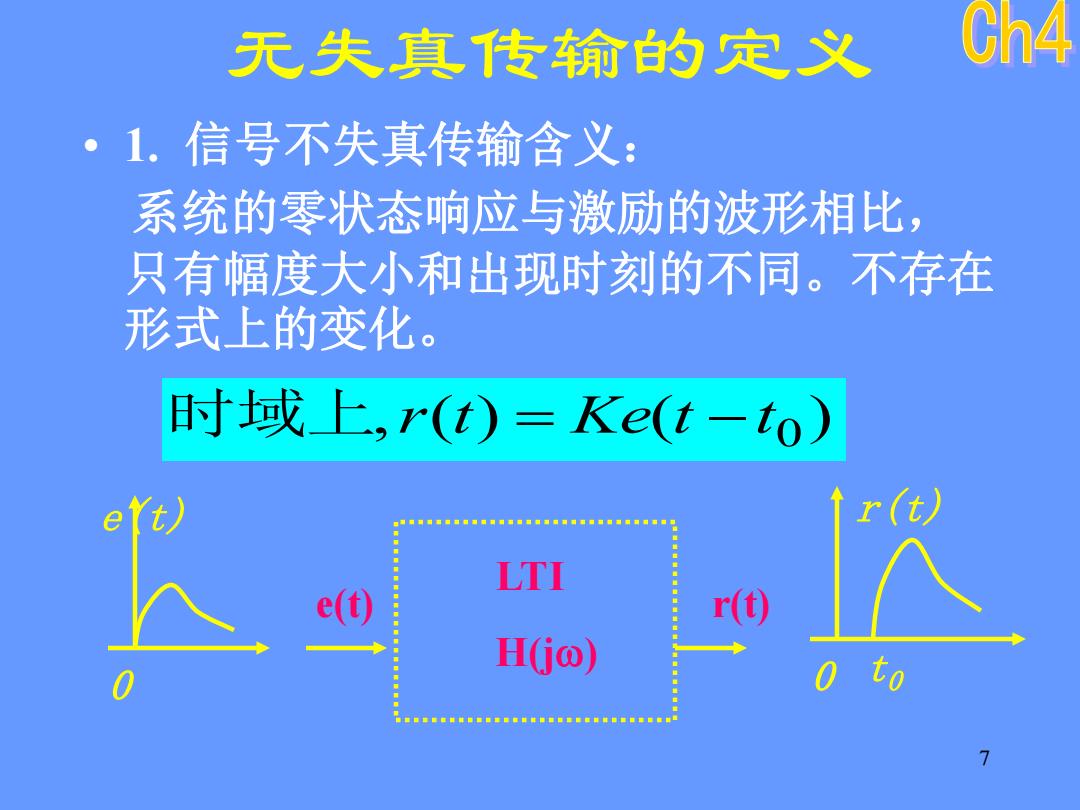
无失真传输的定义 Ch4 。1.信号不失真传输含义: 系统的零状态响应与激励的波形相比, 只有幅度大小和出现时刻的不同。不存在 形式上的变化。 时域上,r(t)=Ke(t-to)》 r( ◆ ◆ LTI H(j@) to 7
7 无失真传输的定义 • 1. 信号不失真传输含义: 系统的零状态响应与激励的波形相比, 只有幅度大小和出现时刻的不同。不存在 形式上的变化。 LTI H(j) r(t) r(t) 0 t0 e(t) e(t) 0 , ( ) ( ) 0 时域上 r t = Ke t −t

2.不失真传输系统的频响H(w): Ch4 寸或,r(t) Ke(t-to) 两边取傅立叶变换e(t)->EGjw),r(t)-->R(jw) R(jo)=KE(iω)ewo 又:若时域中系统冲激响应为(t) r()=e()*h(t) R(iω)=E(iω)H(io) H(jo)-Keja to H(j@)eip(@) 不失真传输 1(iω)=K 系统的频响H(w): (o) =一·to 特点:幅频响应为常数, 相频响应为过原点的直线。 8
8 2. 不失真传输系统的频响H(jw): 时域上,r(t) = Ke(t −t 0 ) • 两边取傅立叶变换e(t)--->E(jw), r(t)---> R(jw) 0 ( ) ( ) j t R j KE j e − = • 又:若时域中系统冲激响应为h(t) r(t) = e(t)*h(t) R( j) = E( j)H( j) ( ) ( ) | ( )| j t 0 j H j = Ke = H j e − 不失真传输 系统的频响H(jw): = − = ( ) 0 | ( )| t H j K 特点:幅频响应为常数, 相频响应为过原点的直线

0h4 H(j@) p(jo) 3.产生失真的原因: a.信号幅度不能等幅放大或衰减一>幅度失真 b.信号的相移不能按比例变化一>相位失真 心.幅度失真和相位失真同时存在一>同时失真 9
9 3. 产生失真的原因: a.信号幅度不能等幅放大或衰减—>幅度失真 b.信号的相移不能按比例变化—>相位失真 c.幅度失真和相位失真同时存在—>同时失真 H( j) ( j) 0 − t
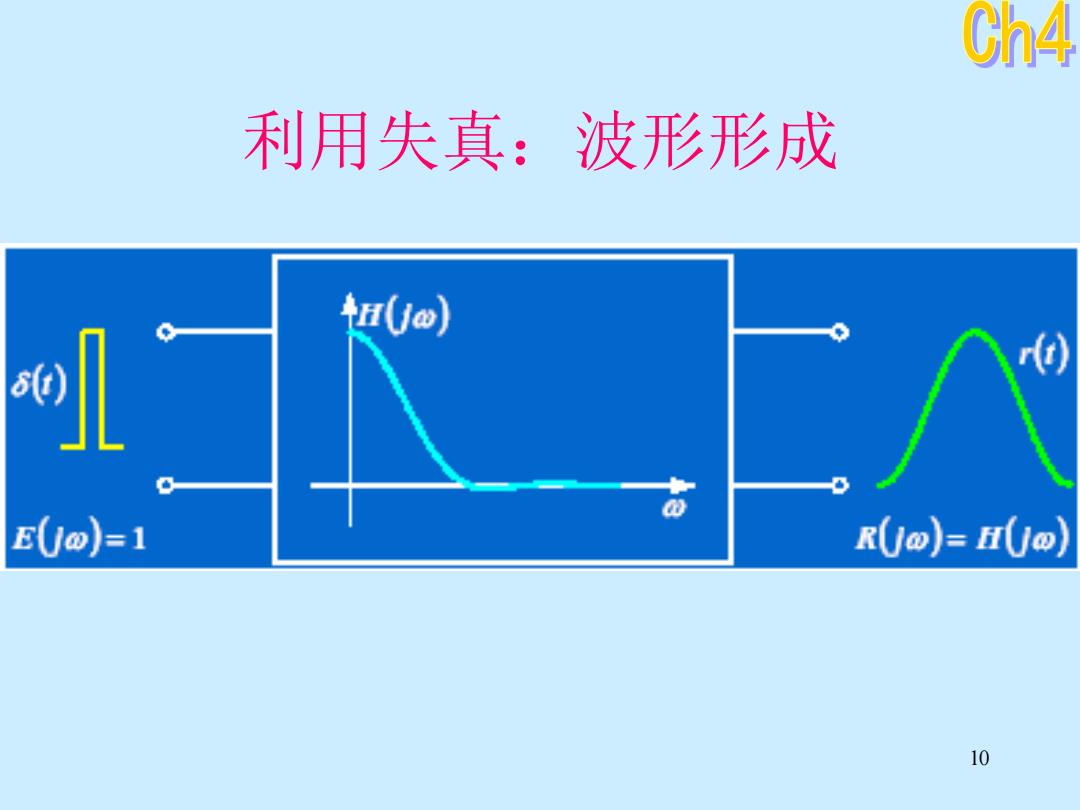
Ch4 利用失真:波形形成 U® r() E(jo)=1 R(jo)=H(jo) 10
10 利用失真:波形形成