华东理工大学：《信号与系统》课程教学资源（课件讲稿）第三章 傅里叶变换 §3.9 Fourier transform of periodic signal（周期FT）

S 3.9 Fourier transform of periodic signal 。一般周期信号的傅立叶变换 傅立叶级数FS与其单脉冲的傅立叶 变换FT的关系 周期矩形脉冲FS与单矩形脉冲FT的 关系 。周期矩形脉冲的FS和FT 。周期单位冲激序列的FS和FT ·正余弦信号的傅立叶变换FT

§3.9 Fourier transform of periodic signal • 一般周期信号的傅立叶变换 • 傅立叶级数FS与其单脉冲的傅立叶 变换FT的关系 • 周期矩形脉冲FS与单矩形脉冲FT的 关系 • 周期矩形脉冲的FS和FT • 周期单位冲激序列的FS和 FT • 正余弦信号的傅立叶变换FT

Recall: 周期信号→非周期信号→周期信号 FS FT FT 周期信号不满足绝对可积条件 引入冲激信号后，冲激的积分是有意义 的 在以上意义下，周期信号的傅立叶变换 是存在的 周期信号FT→周期抽样FT→抽样定理→实际应用

周期信号 Recall: FS FT FT 非周期信号 周期信号 • 周期信号不满足绝对可积条件 • 引入冲激信号后，冲激的积分是有意义 的 • 在以上意义下，周期信号的傅立叶变换 是存在的 周期信号FT周期抽样FT抽样定理实际应用

1、一般周期信号的傅立叶变换 f(t)=∑Fnemo4 n=-00 00 FT[f(t)】=2元∑Fnδ(o-no1) 1n=-o0 。由一些冲激组成离散频谱 ·位于信号的谐频处 大小不是有限值，而是无穷小频带内 有无穷大的频谱值

1、一般周期信号的傅立叶变换 • 由一些冲激组成离散频谱 • 位于信号的谐频处 • 大小不是有限值，而是无穷小频带内 有无穷大的频谱值      n jn t n f t F e 1 ( ) .  [ ( )] 2 ( )  F   n 1 FT f t n   n    

周期信号的傅立叶变换存在条件 周期信号不满足绝对可积条件 引入冲激信号后，冲激的积分是有意义 的 在以上意义下，周期信号的傅立叶变换 是存在的 周期信号的频谱是离散的，其频谱密 度，即傅立叶变换是一系列冲激

周期信号的傅立叶变换存在条件 • 周期信号不满足绝对可积条件 • 引入冲激信号后，冲激的积分是有意义 的 • 在以上意义下，周期信号的傅立叶变换 是存在的 • 周期信号的频谱是离散的，其频谱密 度， 即傅立叶变换是一系列冲激

2、周期信号FS与单脉冲FT的关系 FT[f(t】=2π∑Fnδ(o-no1) n=-o0 F.-)e F)=)ed F

2、周期信号 FS与单脉冲FT的关系    2 2 1 1 1 1 ( ). 1 T T jn t n f t e dt T F     2 1 2 1 ( ) ( ). 0 0 T T F f t e dt jt  1 ( ) 1 0 1    n n F T F   [ ( )] 2 ( )     1 FT f t F n n   n    

F (@) T 1f6() F() =F()l-ne n T

1 ( ) 1 0 1    n n F T F   ( ) F0  0 1 1 F ( ) T  Fn f (t) ( ) 0 f t

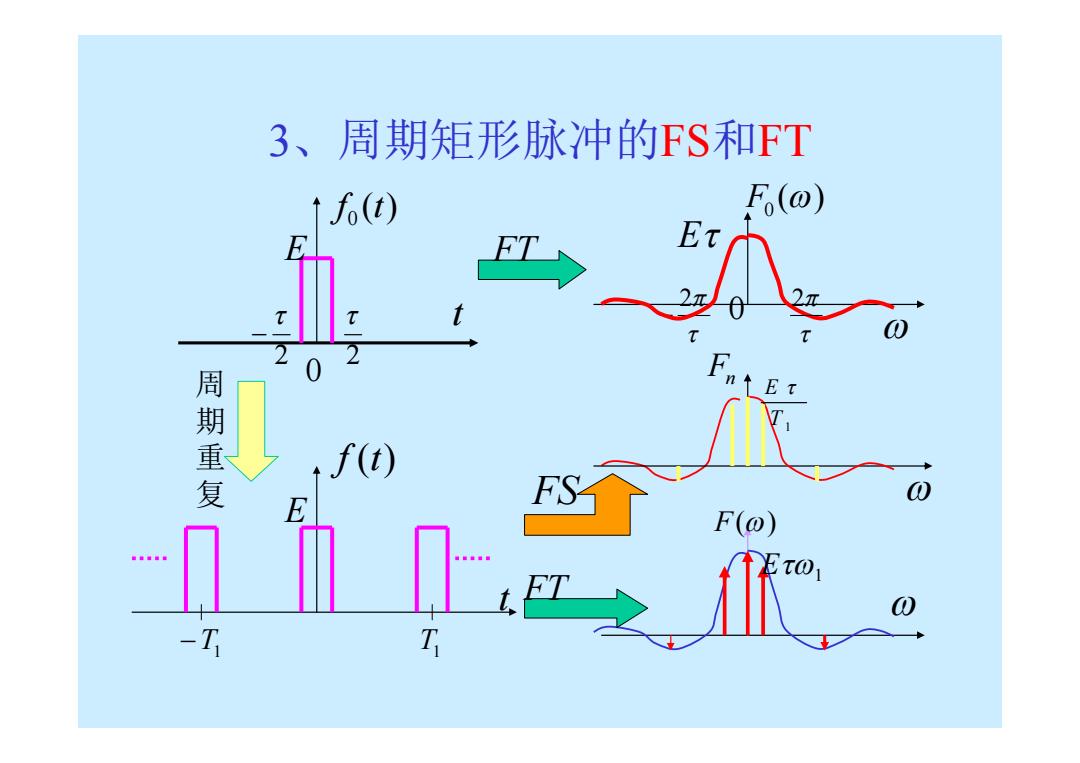
3、周期矩形脉冲的FS和FT ↑f(t) F(@) E 周期重复 f(t) F(⊙) -T T

3、周期矩形脉冲的FS和FT 0 E ( ) 0 f t 2  2   t E ( ) F0    2  2  0 T 1 E  Fn  1 E F()  FT FS FT 周 期 重 复 T1 T1 E f (t) t

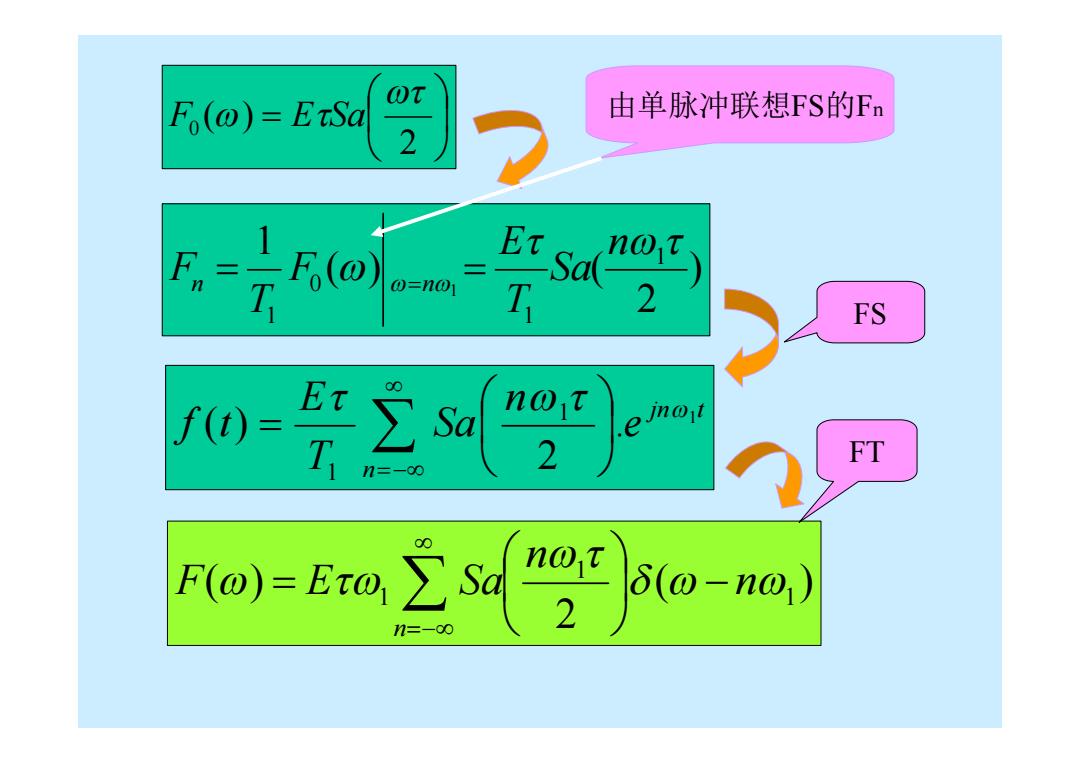
WT Fo(@)=ETSa 由单脉冲联想FS的Fn 2 F=Fo(@) not T 0=n01 T FS w学 FT δ(o-n0)） n=-o∞

       2 ( ) 0  F  ESa ) 2 ( ) ( 1 1 1 0 1 1      n Sa T E F T Fn  n  jn t n e n Sa T E f t 1 . 2 ( ) 1 1               ( ) 2 ( ) 1 1 1       n n F E Sa n            由单脉冲联想FS的Fn FS FT

4、周期单位冲激序列的FS Impulse-train 00 00 ,()=∑6(t-nT)=∑Fe n=-00 n=-00 1 T 8,0-72 1n=-00

4、周期单位冲激序列的FS Impulse-train 1 1 1 ( ) ( ) . jn t T n n n t t nT F e               1 2 1 1 1 2 1 1 1 1 ( ). T T jn t F t e dt n T T T        1 1 1 1 ( ) jn t T n t e T      

5、周期单位冲激序列的FT Impulse-train 8.0定u-0-立em7 00 n=-c0 1n=-g0 00 FT[f(t)]=2π ∑6(o-no,） T n=-o0 00 F(o)=FT[,()]=0∑6(o-no) n=-00

5、周期单位冲激序列的FT Impulse-train 1 1 1 1 1 1 ( ) ( ) . jn t jn t T n n n n t t nT F e e T                     ( ) 1 [ ( )] 2 1 1    n T FT f t n      1 1 1 ( ) [ ( )] ( ) T n F FT t n            