
§1-1-2 常见基本信号 ,指数信号exponential signals ,正弦信号sinusoidal signals Sa(t)信号Sa(t)signal
1 §1-1-2 常见基本信号 •指数信号exponential signals •正弦信号sinusoidal signals •Sa(t)信号Sa(t)signal
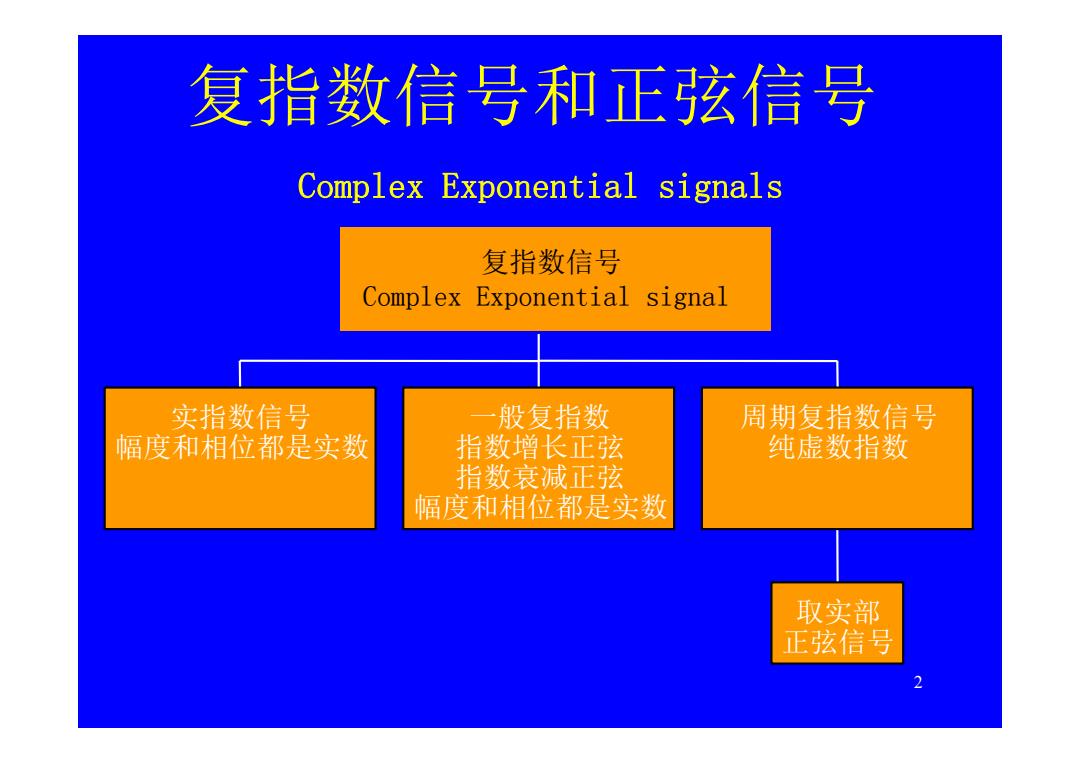
复指数信号和正弦信号 Complex Exponential signals 复指数信号 Complex Exponential signal 实指数信号 般复指数 周期复指数信号 幅度和相位都是实数 指数增长正弦 纯虚数指数 指数衰减正弦 幅度和相位都是实数 取实部 正弦信号 2
2 复指数信号和正弦信号 Complex Exponential signals 实指数信号 幅度和相位都是实数 一般复指数 指数增长正弦 指数衰减正弦 幅度和相位都是实数 取实部 正弦信号 周期复指数信号 纯虚数指数 复指数信号 Complex Exponential signal

复指数信号 ·连续时间复指数信号: x()=C6 ·C为复数 C=a+jβ ·a为复数 a=r+jo
3 复指数信号 • 连续时间复指数信号: • C为复数 • a为复数 a r j C j

实指数信号一C和a都是实数 若 C=+jB中的B为0,C实数 同时 若 a=r+j0中的@为0,a实数 则 ()=CS 为实指数函数
4 实指数信号— C 和 a都是实数 • 若 中的 为 0 , C实数 同时 • 若 中的 为 0 , a实数 则 为实指数函数 a r j C j

实指数信号一C和a都是实数 x(4)=欧Gu r>0 r<0 x()随t的增加 x)随t的增加 而指数增长 而指数衰减 5.. 。9 0.4 0.3 0.2 0
5 • • x(t)随 t 的增加 而指数增长 • • x(t)随 t 的增加 而指数衰减 r 0 r 0 0 2 4 6 8 1 0 1 2 1 4 0 0 . 1 0 . 2 0 . 3 0 . 4 0 . 5 0 . 6 0 . 7 0 . 8 0 . 9 1 0 2 4 6 8 1 0 1 2 1 4 0 5 1 0 1 5 2 0 2 5 3 0 3 5 4 0 4 5 实指数信号— C 和a都是实数

父(E) 笔 周期夏复指数信号一a=±jo ·若a为纯虚数,即 a=+jo时,则 x(t)=e ±j0ot 特点:该信号是周期的,周期为T。 ejat=e/o(+76) 7o= 2π 6
6 周期复指数信号— • 若a 为纯虚数,即 时,则 • 特点:该信号是周期的,周期为T0 a j a j j t x t e 0 ( ) 0 0 0 0 2 0 ( ) e e T j t j t T

正弦信号,一取周期复指数的实部 欧拉公式 )=COs()+jsin(ot+ 取实部则为正弦信号 x(t)=Acos(@t+)
7 正弦信号1—取周期复指数的实部 • 欧拉公式 • 取实部则为正弦信号 cos( ) sin( ) 0 0 ( ) 0 e t j t j t ( ) cos( ) x t A 0 t
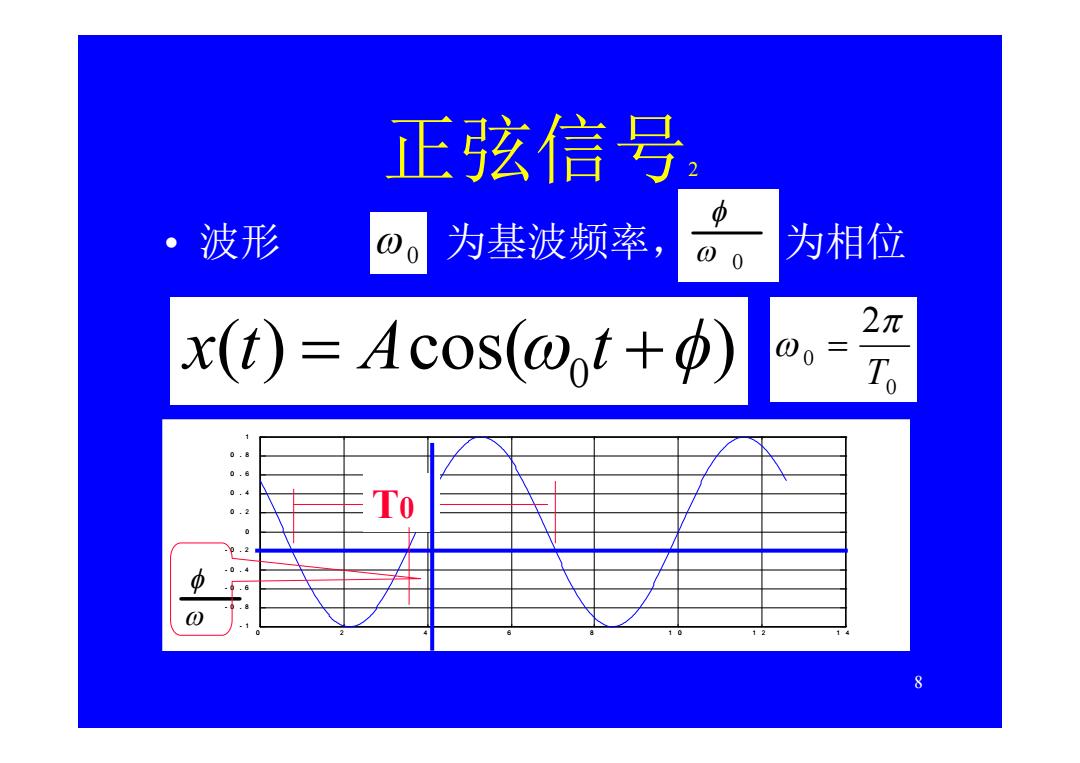
正弦信号 中 ·波形 00 为基波频率 、0 为相位 x(t)=Acos(@t+) 2π T To .2 0.4 .1 8
8 正弦信号2 • 波形 为基波频率, 为相位 ( ) cos( ) x t A 0 t 0 0 0 0 2 T 0 2 4 6 8 1 0 1 2 1 4 - 1 - 0 . 8 - 0 . 6 - 0 . 4 - 0 . 2 0 0 . 2 0 . 4 0 . 6 0 . 8 1 T0

x() CIE 一股复指数信号, 最一般的情况 x(t)=( t+jB )e(r+joo)! C用极座标,a用直角坐标来表示 x(t)=Ce -Cei -Ce"e-0) =Ce"cos(@t+0)+jCe"sin(@t+0) 9
9 一般复指数信号1 • 最一般的情况 • C用极座标,a用直角坐标来表示 r j t x t j e ( ) 0 ( ) ( ) cos( ) sin( ) ( ) 0 0 ( ) ( ) 0 0 Ce t jCe t Ce e x t Ce Ce e rt rt rt j t at j r j t
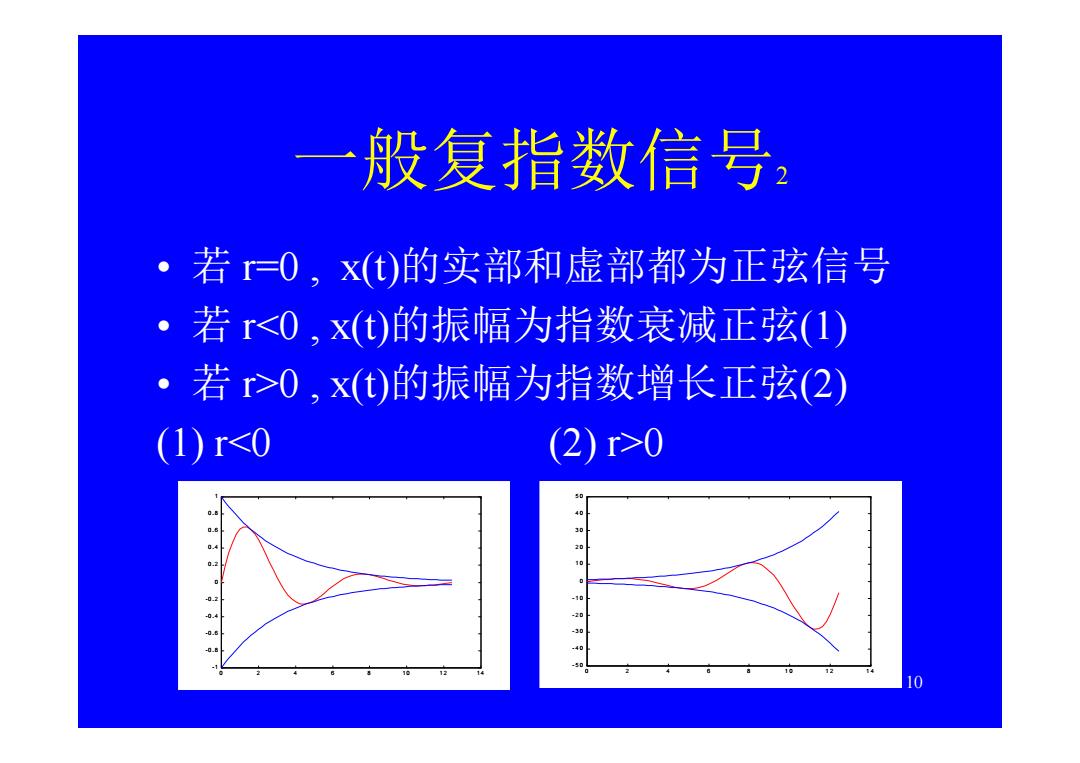
一般复指数信号 ·若=0,x(t)的实部和虚部都为正弦信号 。若r0,x(t)的振幅为指数增长正弦(2) (1)r0 00 10 40 40 10
10 一般复指数信号2 • 若 r=0 , x(t)的实部和虚部都为正弦信号 • 若 r0 , x(t)的振幅为指数增长正弦(2) (1) r0 0 2 4 6 8 1 0 1 2 1 4 -1 -0 . 8 -0 . 6 -0 . 4 -0 . 2 0 0 . 2 0 . 4 0 . 6 0 . 8 1 0 2 4 6 8 1 0 1 2 1 4 - 5 0 - 4 0 - 3 0 - 2 0 - 1 0 0 1 0 2 0 3 0 4 0 5 0