
细台形z幸院 antai Institute of Technology 原城台家人维年能 第九章机械臂的线性控制 四5.1时变位置和姿态的符号表示 四5.2刚体的线速度和角速度 四5.3机器人连杆的运动 四5.4雅可比矩阵 四5.5机械臂中的静力 2
2 5.1 时变位置和姿态的符号表示 5.2 刚体的线速度和角速度 5.3 机器人连杆的运动 5.4 雅可比矩阵 5.5 机械臂中的静力 第九章 机械臂的线性控制

细台形z幸院 antai Institute of Technology 引言 原城台好火维年院 线性控制仅适用于能够用线性微分方程进行 数学建模的系统. a0++a-云a0+ag0=An0++b700x 对于机械臂,这种方法实质上是一种近似的 方法,但是,这种近似通常是可行的,而且是当 前工程实际中最常用的方法
线性控制仅适用于能够用线性微分方程进行 数学建模的系统. 0 1 0 1 ( ) ( ) ( ) ( ) ( ) ( ) n m n n n m m m d d d d a c t a c t a c t b r t b r t b r t dt dt dt dt 对于机械臂,这种方法实质上是一种近似的 方法,但是,这种近似通常是可行的,而且是当 前工程实际中最常用的方法. 引言

细台程2幸优 antai Institute of Technology 反馈与闭环控制 原城台好火维年馆 1.开环控制 (1)由轨迹生成器给定关节角、关节角速度、关节角加 速度。 (2)用指定模型计算所需要的扭矩: x=M(⊙a)8.+V(⊙a,⊙a)+G(a) 如果模型是完备和精确的,且没有噪声或者其它干扰存 在,上式即可实现期望轨迹. Q,⑧,g 轨迹发生器 动力学 机械臂
1. 开环控制 (1)由轨迹生成器给定关节角、关节角速度、关节角加 速度。 (2)用指定模型计算所需要的扭矩: 如果模型是完备和精确的,且没有噪声或者其它干扰存 在,上式即可实现期望轨迹. ( ) ( , ) ( ) M d d V d d G d , , 轨迹发生器 动力学 机械臂 , , d d d d 反馈与闭环控制

细台形z幸院 antai Institute of Technology 反馈与闭环控制 原城台好火维年院 然而在实际情况下,由于动力学模型的不理 想以及不可避免的干扰使得这个方案并不实用。 这种控制技术称为开环控制方式,因为没有 利用关节传感器的反馈
然而在实际情况下,由于动力学模型的不理 想以及不可避免的干扰使得这个方案并不实用。 这种控制技术称为开环控制方式,因为没有 利用关节传感器的反馈。 反馈与闭环控制

细台形2幸院 antai Institute of Technology 反馈与闭环控制 原城台好火维年航 2.闭环系统 建立高性能的控制系统的唯一方法就是利用关 节传感器的反馈。 伺服误差: E=⊙-,E=© -⊙ 这样,控制系统就能够根据伺服误差函数计算 驱动器需要的力矩。这个基本思想是通过计算驱动 器的扭矩来减少伺服误差
2. 闭环系统 建立高性能的控制系统的唯一方法就是利用关 节传感器的反馈。 伺服误差: 这样,控制系统就能够根据伺服误差函数计算 驱动器需要的力矩。这个基本思想是通过计算驱动 器的扭矩来减少伺服误差。 , E d E d 反馈与闭环控制
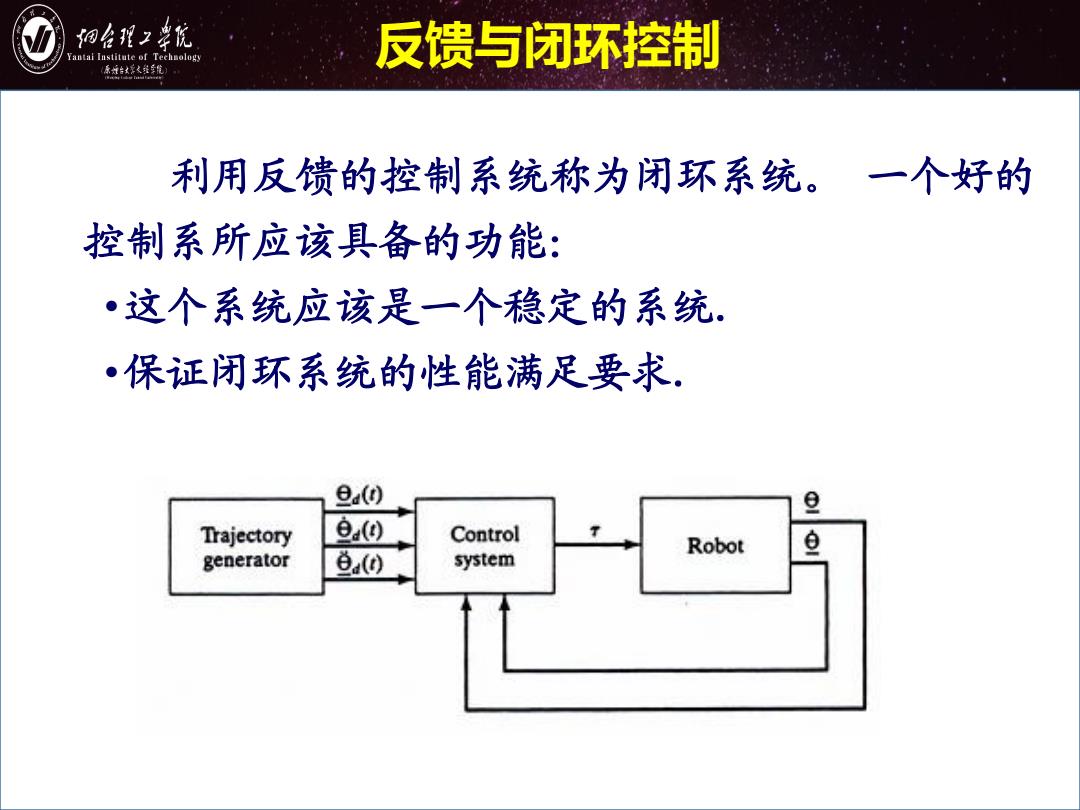
细台形z幸院 antai Institute of Technology 反馈与闭环控制 原城台家之金年院 利用反馈的控制系统称为闭环系统。一个好的 控制系所应该具备的功能: •这个系统应该是一个稳定的系统 ·保证闭环系统的性能满足要求. 旦(0 旦 Trajectory 8u0 Control Robot generator 色(0 system
利用反馈的控制系统称为闭环系统。 一个好的 控制系所应该具备的功能: •这个系统应该是一个稳定的系统. •保证闭环系统的性能满足要求. 反馈与闭环控制
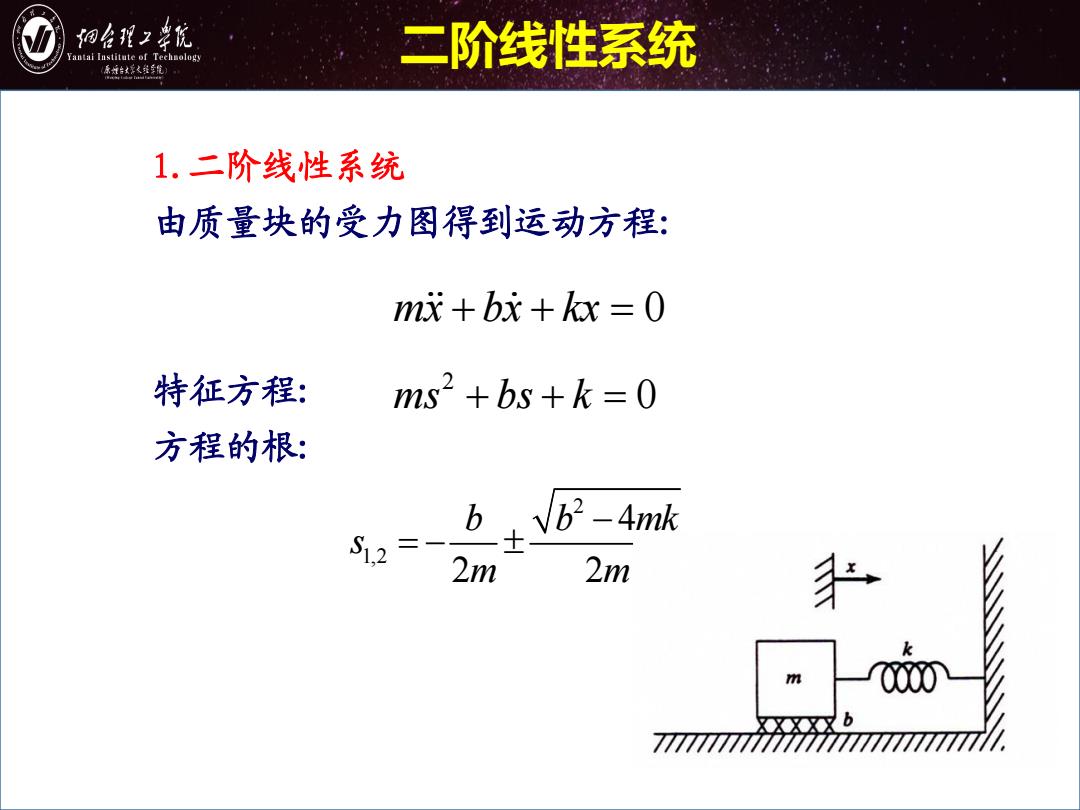
细台形2幸院 antai Institute of Technology 二阶线性系统 原城台好火维年航 1.二阶线性系统 由质量块的受力图得到运动方程: mx+bx+kx=0 特征方程: ms2 +bs+k 0 方程的根: 2=- 2m 2m ●XXX又b
1.二阶线性系统 由质量块的受力图得到运动方程: 特征方程: 方程的根: 2 1,2 4 2 2 b b mk s m m mx bx kx 0 2 ms bs k 0 二阶线性系统

细台程2幸优 antai Institute of Technology 二阶线性系统 承城台大家《维单能 一种描述二阶振动系统的两个参数是阻尼比(damping ratio)and固有 频率(natural frequency): s2+250nS+0=0 0=-51wn 衰减系数 Re Wa wv1-52 阻尼振荡频率 对于有阻尼的质量弹簧系统,阻尼比和固有频率分别为: b = 2√amn @=k/m 当无阻尼时(b=)0阻尼比为0;对于临界阻尼(b2=4阻尼比是1
一种描述二阶振动系统的两个参数是 阻尼比 ( damping ratio )and 固有 频率(natural frequency) : 对于有阻尼的质量-弹簧系统,阻尼比和固有频率分别为: 当无阻尼时 ( ), 阻尼比为0; 对于临界阻尼 ( ), 阻尼比是 1 . 2 2 2 0 n n s s 2 1 n d n w w w , / 2 n b k m km b 0 2 b 4km 衰减系数 阻尼振荡频率 二阶线性系统
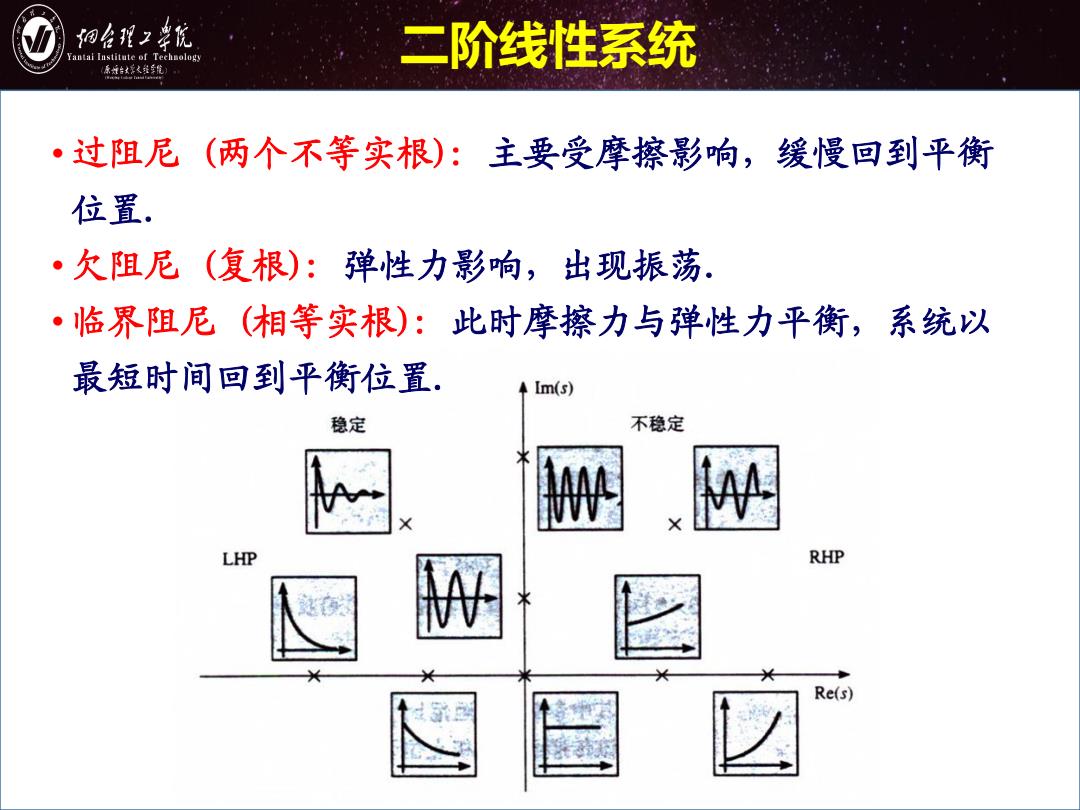
细台形2幸院 antai Institute of Technology 二阶线性系统 原城台好火维年航 ·过阻尼(两个不等实根):主要受摩擦影响,缓慢回到平衡 位置. ·欠阻尼(复根):弹性力影响,出现振荡. ·临界阻尼(相等实根):此时摩擦力与弹性力平衡,系统以 最短时间回到平衡位置. 4 Im(s) 稳定 不稳定 LHP RHP Re(s)
• 过阻尼 (两个不等实根): 主要受摩擦影响,缓慢回到平衡 位置. • 欠阻尼 (复根): 弹性力影响,出现振荡. • 临界阻尼 (相等实根): 此时摩擦力与弹性力平衡,系统以 最短时间回到平衡位置. 二阶线性系统
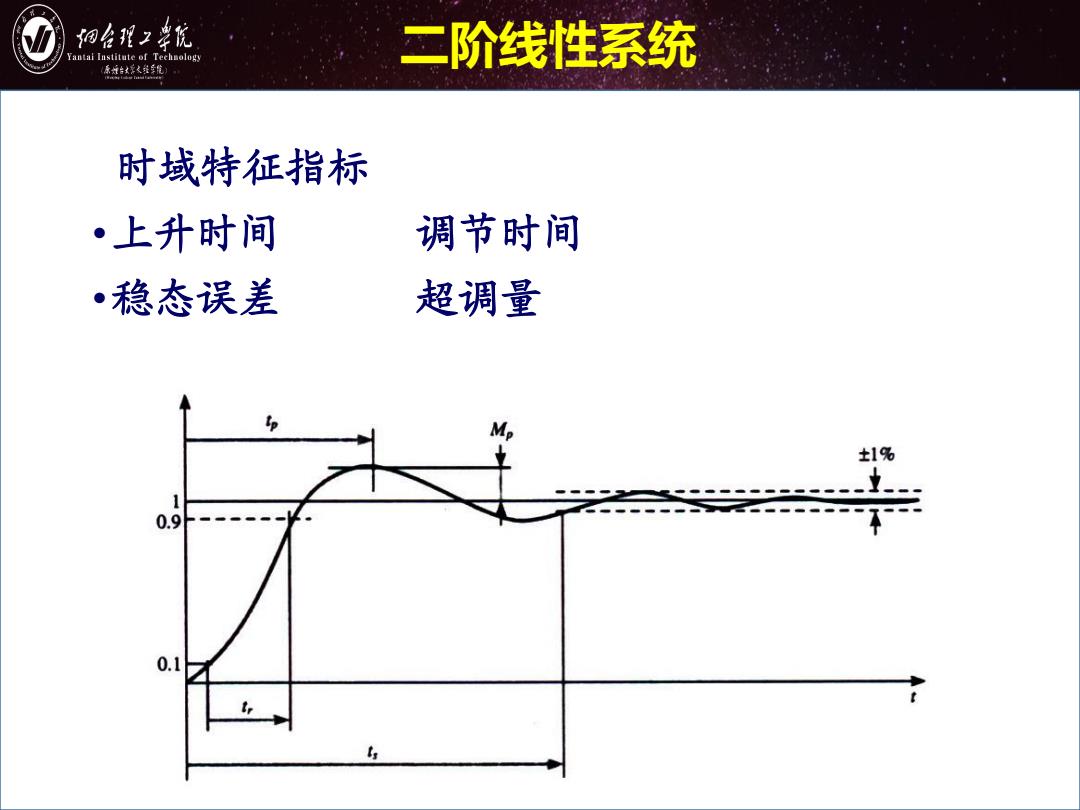
细台形2幸院 antai Institute of Technology 二阶线性系统 原城台好父维年航 时域特征指标 ·上升时间 调节时间 •稳态误差 超调量 p Mp 1% 1 0.9 0.1
时域特征指标 •上升时间 调节时间 •稳态误差 超调量 二阶线性系统