自动控制原理 3-5线性系统稳定性分析 1.稳定性的基本概念 任何系统在扰动作用下都会偏离原平: 偏差。所谓稳定性,是指系统在扰动: 差状态恢复到原平衡状态的能力。 a点为稳定平衡点 d点为不稳定平衡点
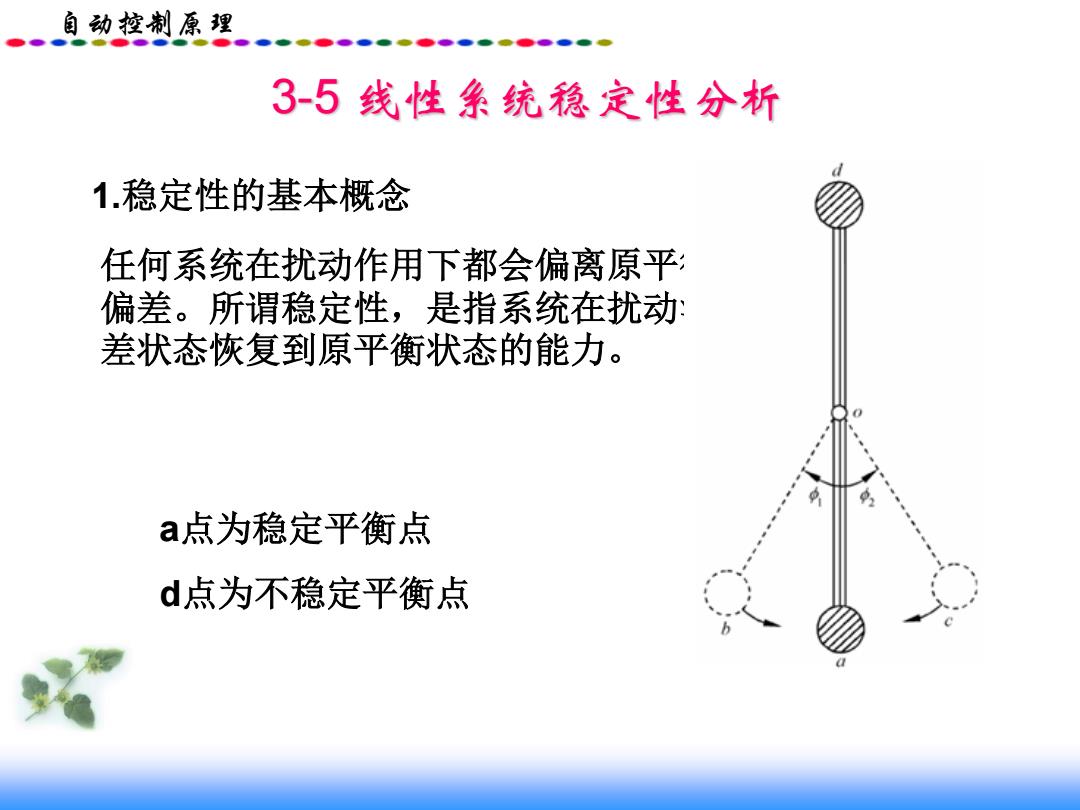
自动控制原理 3-5 线性系统稳定性分析 1.稳定性的基本概念 任何系统在扰动作用下都会偏离原平衡状态,产生初始 偏差。所谓稳定性,是指系统在扰动消失后,由初始偏 差状态恢复到原平衡状态的能力。 a点为稳定平衡点 d点为不稳定平衡点

自动控制原理 大范围稳定的系统: 不论扰动引起的初始偏差有多大,当扰动消失后,系统都 能以足够的准确度恢复到原平衡状态,则称该系统为大范 围稳定的系统。 小范围稳定的系统: 当扰动引起的初始偏差小于某一范围时,扰动消失后,系 统才能恢复到原平衡状态,否则不能恢复到原平衡状态, 则称该系统为小范围稳定的系统。 稳定的线性系统,都是大范围稳定的系统。 非线性系统才存在小范围稳定而大范围不稳定的情 况
自动控制原理 大范围稳定的系统: 不论扰动引起的初始偏差有多大,当扰动消失后,系统都 能以足够的准确度恢复到原平衡状态,则称该系统为大范 围稳定的系统。 小范围稳定的系统: 当扰动引起的初始偏差小于某一范围时,扰动消失后,系 统才能恢复到原平衡状态,否则不能恢复到原平衡状态, 则称该系统为小范围稳定的系统。 稳定的线性系统,都是大范围稳定的系统。 非线性系统才存在小范围稳定而大范围不稳定的情 况

自动控制原理 二、系统稳定的充要条件: 闭环极点严格位于S左半平面。 对线性定常系统,零初始条件下,若其脉冲响应收 敛,则系统稳定,否则不稳定。 bnsm+…+bo C(S)=Φ(S)·1= (s-S,f(s2+25oks+®) i=1 BS+C +s2+25wA5+o2 a0-2e”+2成evio4+g)
自动控制原理 对线性定常系统,零初始条件下,若其脉冲响应收 敛,则系统稳定,否则不稳定。 二、系统稳定的充要条件: 闭环极点严格位于S左半平面。 1 2 1 2 0 2 2 1 1 2 2 1 1 ( ) (s) 1 ( ) ( 2 ) 2 m m n n j k nk nk j k n n j k k j k j k nk nk b s b C s s s s s A B s C s p s s = = = = + + = = − + + + = + − + + 1 2 ' 1 1 ( ) sin( ) j k n n s t t j k dk k j k c t A e B e t − = = = + +
自动控制原理 即单位脉冲响应为: c(0)=之A,e+2B,e'sin(out+A) k=1 系统稳定 222222涂涂次22222涂2次222 lim c(t)=0 t→∞ 综上所述,要判断 一个系统是否稳定,取决于系统 的全部特征根。课本P110下部 线性系统稳定的充要条件:闭环系统特征方程的所 有根均具有负实部:或者说, 闭环传递函数的极点 均位于左半s平面
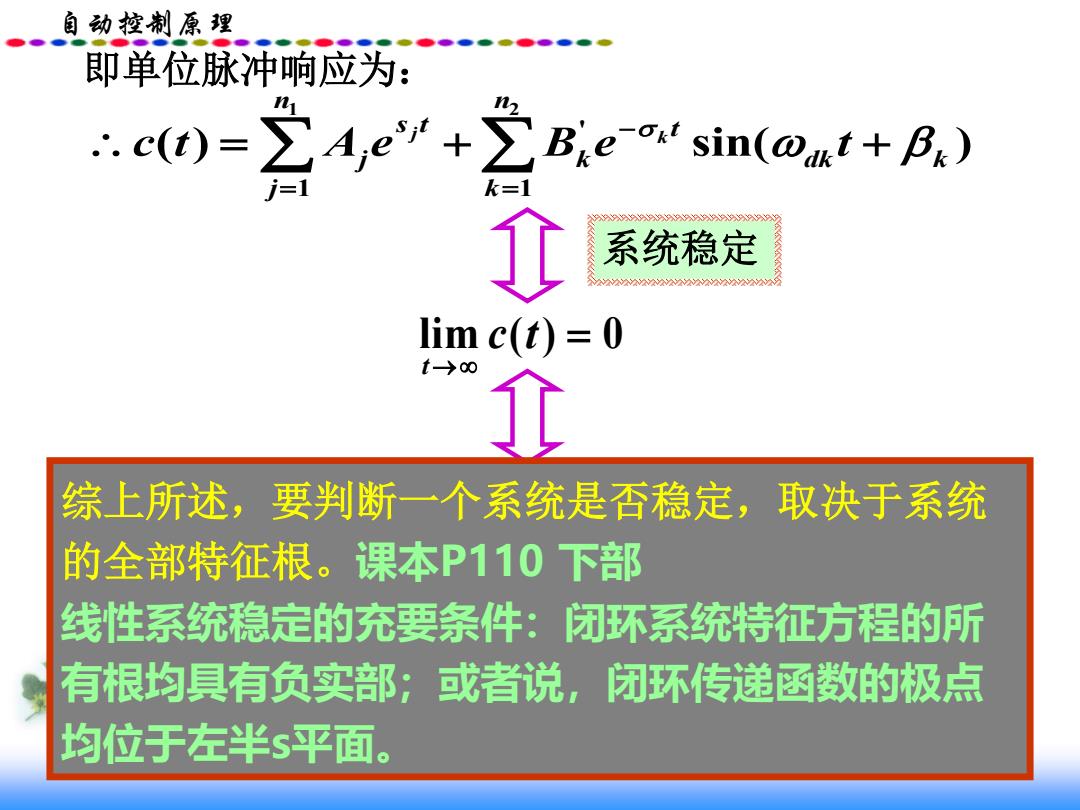
自动控制原理 lim ( ) 0 t c t → = 即单位脉冲响应为: 系统稳定 1 2 ' 1 1 ( ) sin( ) j k n n s t t j k dk k j k c t A e B e t − = = = + + j s 为负实数 − k 为负实部 综上所述,要判断一个系统是否稳定,取决于系统 的全部特征根。课本P110 下部 线性系统稳定的充要条件:闭环系统特征方程的所 有根均具有负实部;或者说,闭环传递函数的极点 均位于左半s平面

自动控制原理 3.劳思稳定判据 anS”+an-1S"-+…+4S+=0 (1)系统稳定的必要条件是特征方程的所有系数,>0 均大于零。 若不满足系统必定不稳定,若满足系统未必稳定。 (2)列劳思表 线性系统稳定的充要条件是劳思表中第一列所有 项系数均大于零。 第一列中系数符号变化次数为极点在右半平面的 个数
自动控制原理 3.劳思稳定判据 (1)系统稳定的必要条件是特征方程的所有系数ai>0 均大于零。 若不满足系统必定不稳定,若满足系统未必稳定。 (2)列劳思表 线性系统稳定的充要条件是劳思表中第一列所有 项系数均大于零。 第一列中系数符号变化次数为极点在s右半平面的 个数。 1 1 1 0 0 n n n n a s a s a s a − + + + + = −

自动控制原理 劳斯表的列法 特征方程为:D(s)=a,S5+a4s4+a4S3+a2s2+as+4 as as a 04 02 ao asa;-asaz=b a4a1-45=b2 04 Aa baz-abz=c b 00 cbz-biao d 0 C do
自动控制原理 5 4 3 2 1 5 4 3 2 1 0 D s a s a s a s a s a s a ( ) = + + + + + 0 0 1 1 1 1 2 1 0 1 0 1 2 1 2 4 2 2 4 4 1 5 0 1 4 3 4 3 5 2 4 5 3 5 0 0 2 0 4 1 s a d c c b b a s c a b b a a b s b a a a a a b a a a a a ss a a a s a a a = − = − = − = − 特征方程为: 劳斯表的列法

自动控制原理 例题3-7D()=5+2s3+3s2+4s+5=0,判定稳定性及在右半平 面根的个数。 夏 33 5 22 41 3 2×3-1×4 =1 2×5-1×0 =5 2 2 S 1×4-2×5 =-6 0 1 s 5 系统不稳定,劳斯表第一列变号两次,有两 个闭极点在S右半平面
自动控制原理 432 例题3-7 D s s s s s ( ) 2 3 4 5 0 = + + + + = ,判定稳定性及在右半平 面根的个数。 4 3 2 1 0 s s s s s 系统不稳定,劳斯表第一列变号两次,有两 个闭极点在s右半平面。 1 3 5 240 2 3 1 4 2 5 1 0 =1 =5 2 2 − − 1 4 2 5 =-6 0 1 − 5

自动控制原理 4、劳思判据特殊情况 1、某行首元素为0,其余元素不全为0 为负数,故系 统有两个S右 ①乘因子(s+a),a为任意正数。 半平面的根 ②以无穷小的整数ε替代。 例题2:D(s)=s3-3s+2=0,判定s右半平面 环根的 个数。 S3 1 -3 s3 1 3 s2 0 2 s2 (0)E 2 S1 oo s1 -3E-2)/E S0 2
自动控制原理 4、劳思判据特殊情况 1、某行首元素为0,其余元素不全为0 ①乘因子 (s+a),a为任意正数。 ②以无穷小的整数ε替代。 例题2: ,判定s右半平面中闭环根的 个数。 s 3 1 -3 s 2 0 2 s 1 ∞ s 0 s 3 1 -3 s 2 (0)ε 2 s 1 (-3ε-2)/ε s 0 2 3 D s s s ( ) 3 2 0 = − + = 为负数,故系 统有两个s右 半平面的根
自动控制原理 2、在劳斯阵列表中,出现全零行,则表明在平面 存在关于原点对称的特征根(如一对符号相反的实根、 一对共轭纯虚根或关于实轴对称的两对共轭复根)。 解决办法: 由全零行的上一行构筑辅助方程,将辅助方程导方 程的系数替代全零行继续计算。 由辅助方程可求得关于原点对称的特征根
自动控制原理 2、在劳斯阵列表中,出现全零行,则表明在s平面 存在关于原点对称的特征根(如一对符号相反的实根、 一对共轭纯虚根或关于实轴对称的两对共轭复根)。 解决办法: 由全零行的上一行构筑辅助方程,将辅助方程导方 程的系数替代全零行继续计算。 由辅助方程可求得关于原点对称的特征根

、 自动控制原理 补例:用劳斯判据分析系统的稳定性。 看P113 55+54+3s3+3s2+25+2=0 例题3-8 解: 1 3 2 S 1 3 2 0 全0行 由Q(s)=s+3s2+2=(s2+1)(s2+2)=0 得关于原点对称的根为:±j,±V2j 0 系统特征根为:j,±√2,1
自动控制原理 5 4 3 2 s s s s s + + + + + = 3 3 2 2 0 解: 2 3 2 0. 4 6 0. 2 2 6(0) 3 3 2 3 2 2 3 4(0) 1 1 4 2 3 0 1 2 3 4 5 s + s + = s + s = s s s s s s 辅方: 求导: 4 2 2 2 由 Q s s s s s ( ) 3 2 ( 1)( 2) 0 = + + = + + = 得关于原点对称的根为: j j , 2 0 0 全0行 补例: 用劳斯判据分析系统的稳定性。 看P113 例题3-8 系统特征根为: j j , -1 2