
自动控荆原理 第五章 频域分折法一频率法 5-3 频域稳定判据 奈氏(Nyquist)判据和对数频率稳定判据(奈 氏判据在伯德图上的应用)是常用的两种频 域稳定判据。 频域稳定判据的特点是根据开环系统频率特 性曲线判定闭环系统的稳定性
自动控制原理 第五章 频域分析法-频率法 5-3 频域稳定判据 奈氏(Nyquist)判据和对数频率稳定判据(奈 氏判据在伯德图上的应用)是常用的两种频 域稳定判据。 频域稳定判据的特点是根据开环系统频率特 性曲线判定闭环系统的稳定性
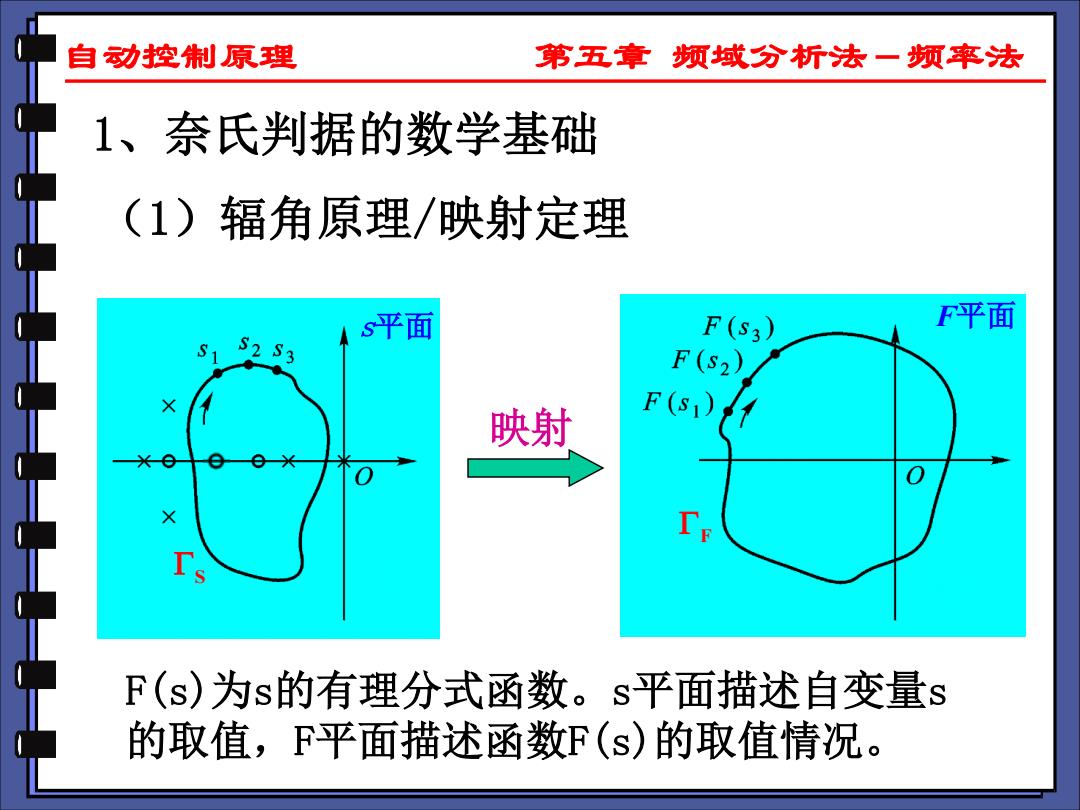
自动控荆原理 第五章频域分析法一频率法 1、奈氏判据的数学基础 (1)辐角原理/映射定理 s平面 F(s3) F平面 F(S2) 映射 F(s1) F(s)为s的有理分式函数。s平面描述自变量s 的取值,F平面描述函数F(s)的取值情况
自动控制原理 第五章 频域分析法-频率法 1、奈氏判据的数学基础 (1)辐角原理/映射定理 映射 F平面 F F(s)为s的有理分式函数。s平面描述自变量s 的取值,F平面描述函数F(s)的取值情况。 s平面 S

自动控原理 第五章频域分析法一频率法 辐角原理:若T包围了Fs)的Z个零点和P个极点,当s 顺时针沿T取值一周时,T绕原点转过R圈。其中 R=P-Z R>O,逆时针包围原点;R<O,顺时针;R=O,不包围。 (注意:工,不穿过F的零极点) 判别系统的稳定性实质就是判别系统在s右半平 面有无闭环极点。 那么如何将辐角定理应用于稳定性判别?
自动控制原理 第五章 频域分析法-频率法 辐角原理:若s包围了F(s)的Z个零点和P个极点,当s 顺时针沿s取值一周时, F绕原点转过R圈。其中 R= P – Z R>0,逆时针包围原点;R<0,顺时针;R=0,不包围。 (注意: s不穿过F(s)的零极点) 判别系统的稳定性实质就是判别系统在s右半平 面有无闭环极点。 那么如何将辐角定理应用于稳定性判别?
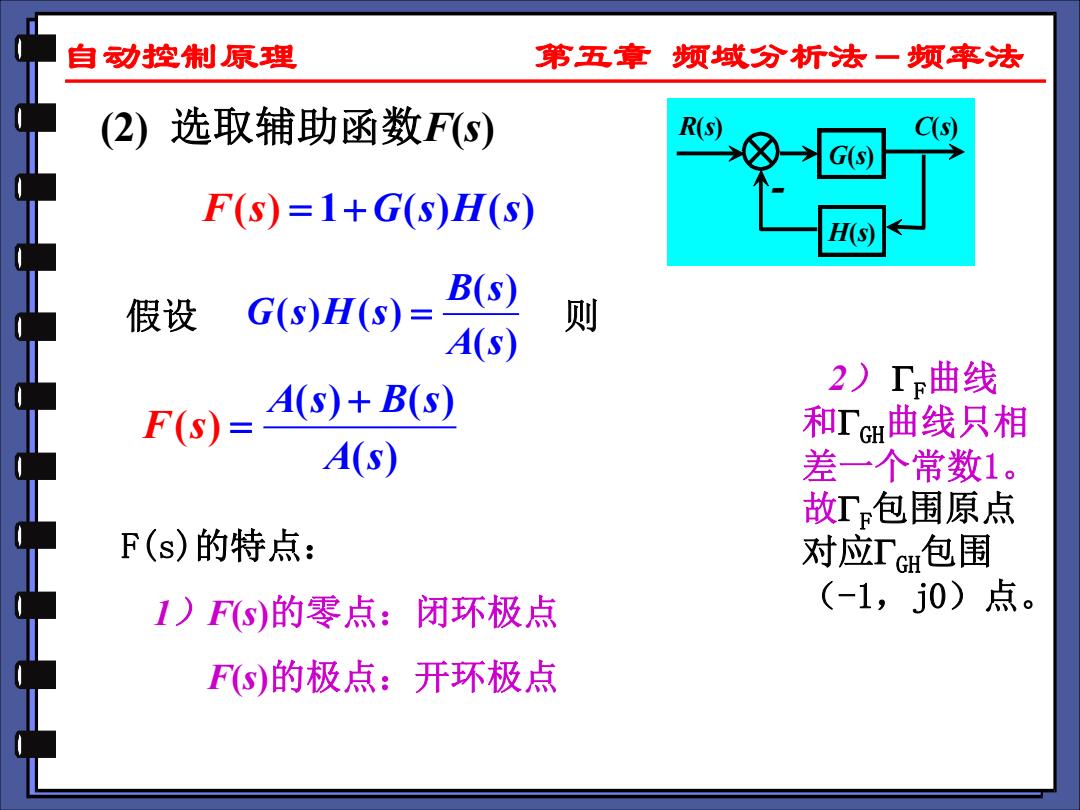
自动控制原理 第五章 频域分析法一频率法 (2)选取辅助函数Fs) R(s) C(s) F(s)=1+G(S)H(S) H(s 假设G(s)H(S)= B(s) 则 A(s) A(s)+B(s) 2)曲线 F(s)= 和T曲线只相 A(s) 差一个常数1。 故T包围原点 F(s)的特点: 对应TGH包围 1)F(s)的零点:闭环极点 (-1,j0)点。 F(s)的极点:开环极点
自动控制原理 第五章 频域分析法-频率法 (2) 选取辅助函数F(s) R(s) G(s) H(s) C(s) - F(s) = +1 ) ( G(s H s) 假设 ( ) ( ) ( ) ( ) B s G s H s A s = 则 ( ) ( ) ( ) ( ) F s A s B s A s + = 1)F(s)的零点:闭环极点 F(s)的极点:开环极点 F(s)的特点: 2) F曲线 和GH曲线只相 差一个常数1。 故F包围原点 对应GH包围 (-1,j0)点
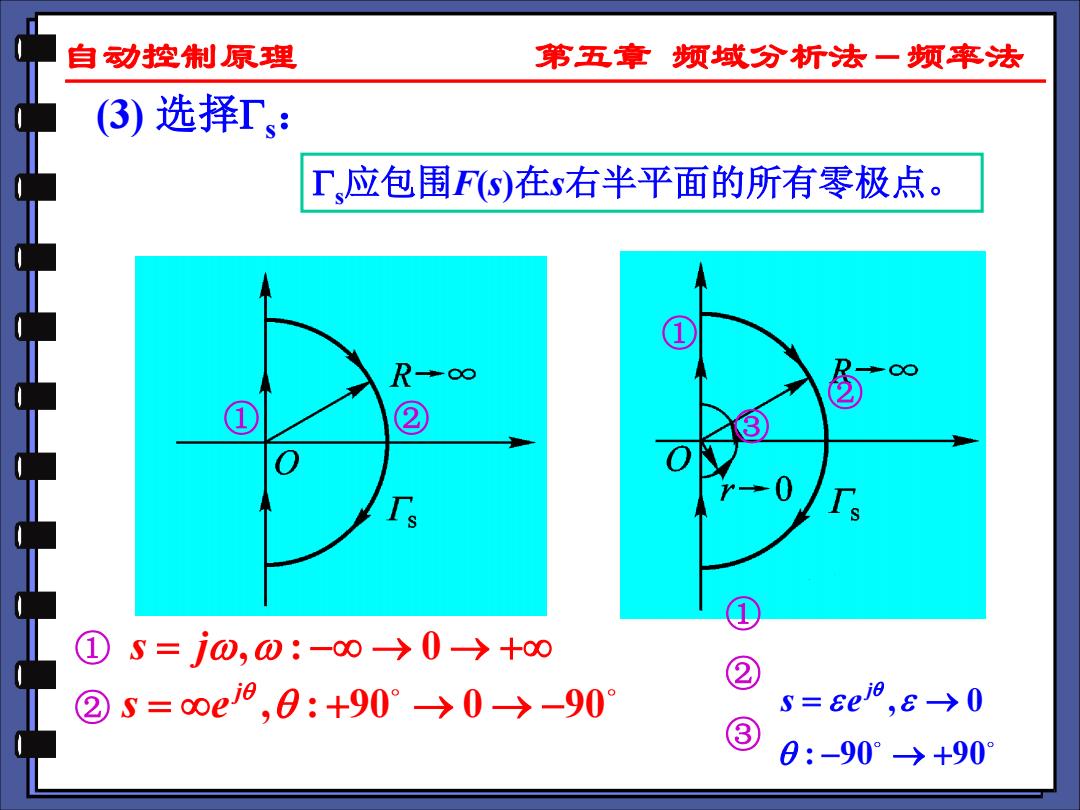
自动控制原理 第五章频域分析法一频率法 (3)选择Ts: T应包围Fs)在s右半平面的所有零极点。 R→o∞ ② ①S=j0,0:-0-→0→+0 ② ② s=ooe8,0:+90°→0→-90 s=6e9,s→0 ③ 0:-90°→+90
自动控制原理 第五章 频域分析法-频率法 (3) 选择s: s应包围F(s)在s右半平面的所有零极点。 ① ② ① s j = − → → + , : 0 ② , : 90 0 90 j s e = + → → − ③ ① ② ① ② ③ , 0 : 90 90 j s e = → − → +

自动控荆原理 第五章 (4)G(s)H(s)曲线的绘制 R→∞ 先来考察第一种情况的Γ、: ①虚轴(s=j0) 其在G(s)Hs)平面上的映射为GGo)HGo),o取值为- 00→十00。 ②无穷大半圆: 其在G(s)H(s)平面上映射为G(jo)H(jo)的终点。 因此,闭合的Γcu就是开环幅相曲线及其镜像
自动控制原理 第五章 频域分析法-频率法 ②无穷大半圆: 其在G(s)H(s)平面上映射为G(jω)H(jω)的终点。 先来考察第一种情况的s: ①虚轴(s=j) 其在G(s)H(s)平面上的映射为G(jω)H(jω),ω取值为- ∞→+∞。 (4) G(s)H(s)曲线的绘制 因此,闭合的GH就是开环幅相曲线及其镜像

自动控荆原理 第五章频域 R→o∞ 考察有积分环节的Γ: ③无穷小半圆 s=6ei0,6→0,0:-90°→+90° 其在G(S)H(S)平面上映射为无穷大圆弧。 K =ooei(-v0) 模值为∞,相角:v*90°→v*(-90°) 顺时针方向 0:0→0+ 顺时针补画v/2个无穷大圆, 0:0*-→0 逆时针补画v/4个无穷大圆
自动控制原理 第五章 频域分析法-频率法 ③无穷小半圆 考察有积分环节的s: 0 ( ) ( ) ( ) ( ) s j j K K G s H s e s e − → = = 模值为∞,相角:v*90°→v*(-90°) 顺时针方向 , 0, : 90 90 j s e = → − → + 其在G(s)H(s)平面上映射为无穷大圆弧。 : 0 0 − + → 顺时针补画v/2个无穷大圆. : 0 0 + → 逆时针补画v/4个无穷大圆
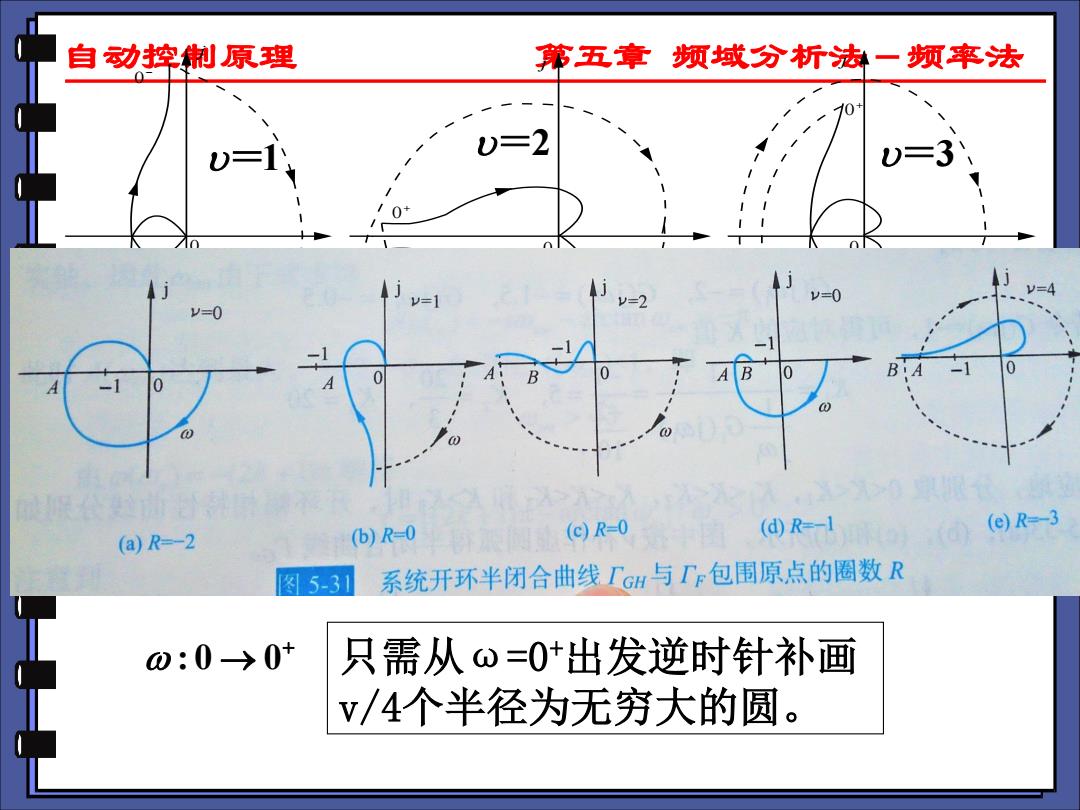
自动控制原理 第五章频域分析法一频率法 0=2 )三3 V=0 y=0 (④R=l (e)R=-3 (aR-2 (b)R-0 (c)R=0 图5-31 系统开环半闭合曲线TGH与TF包围原点的圈数R 0:0→0+ 只需从0=0+出发逆时针补画 v/4个半径为无穷大的圆
自动控制原理 0 − 第五章 频域分析法-频率法 − 0 − 0 + 0 + 0 + 0 j j j 0 0 0 =2 =1 =3 = 0 = 0 = 0 : 0 0 → + 只需从ω=0+出发逆时针补画 v/4个半径为无穷大的圆

自动控原理 第五章 频域分折法一频率法 2、奈氏判据 形式1 ◆R=P-Z→Z=P-R 当Z=0时闭环系统稳定,否则系统不稳定。 ①P:开环传函在s右半平面的极点个数; ②R:当o从-∞→+∞变化时,其奈奎斯特 曲线及其镜像对(-1,j0)点的包围圈数。 ③Z:闭环极点在s右半平面的个数。 系统稳定吗? 0=-00 0=十60 稳定 P=1
自动控制原理 第五章 频域分析法-频率法 2、奈氏判据——形式1 ◆R=P-Z →Z=P-R 当Z=0时闭环系统稳定,否则系统不稳定。 ①P:开环传函在s右半平面的极点个数; ②R:当ω从-∞→+∞变化时,其奈奎斯特 曲线及其镜像对(-1,j0)点的包围圈数。 ③Z:闭环极点在s右半平面的个数。 = + = − = 0 −2 −1 j P = 1 系统稳定吗? 稳定
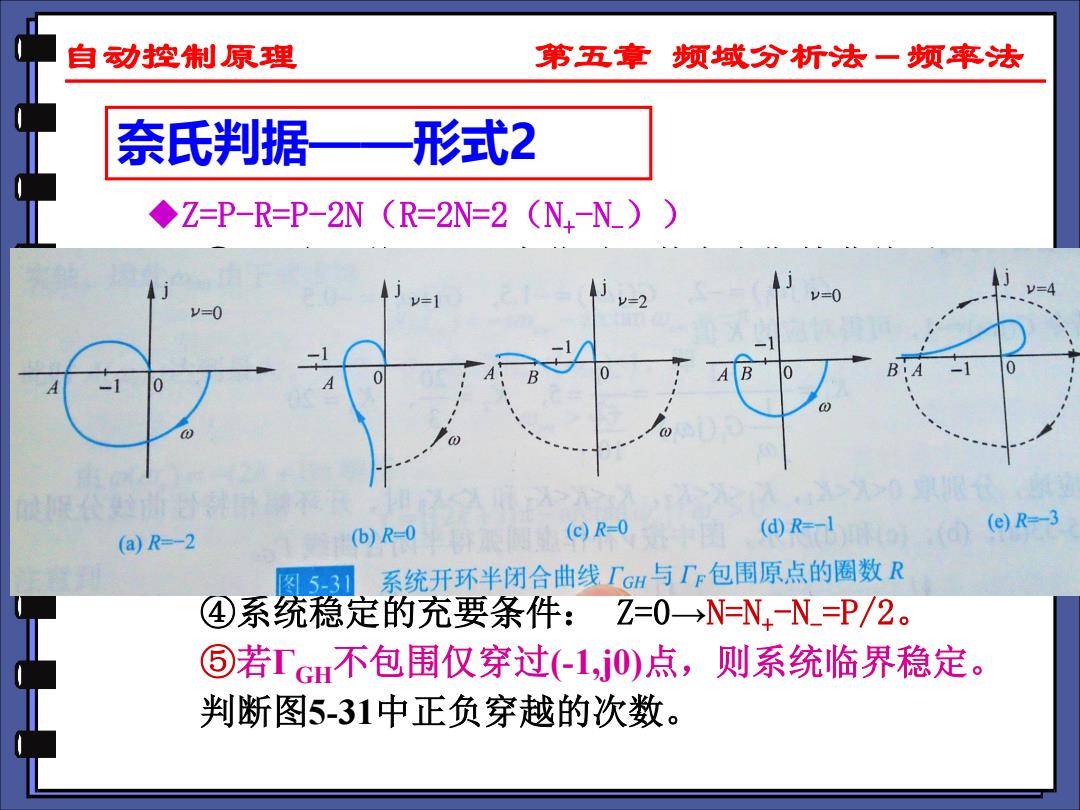
自动控原理 第五章频域分析法一频率法 奈氏判据 形式2 Z=P-R=P-2N (R=2N=2 (N.-N_) =0 y=0 (b)R-0 (c)R=0 (d)R--1 (e)R=-3 (a)R-2 图5-3 系统开环半闭合曲线TGH与T包围原点的圈数R ④系统稳定的充要条件:Z=0→NNN=P/2。 ⑤若Tc不包围仅穿过(-1,j0)点,则系统临界稳定。 判断图5-31中正负穿越的次数
自动控制原理 第五章 频域分析法-频率法 奈氏判据——形式2 ◆Z=P-R=P-2N(R=2N=2(N+-N-)) ①N:当ω从0→+∞变化时,其奈奎斯特曲线对 (-1,j0)点的包围圈数。 ②N:N=N+-N-(对应课本P193 (5)R的计算) i)N+:正穿越次数和(相角/象限数增加) ii)N-:负穿越次数和(相角/象限数减小) ③半次穿越:起始于/终止于负实轴上(-∞,-1) 的穿越。 ④系统稳定的充要条件: Z=0→N=N+-N-=P/2。 ⑤若ГGH不包围仅穿过(-1,j0)点,则系统临界稳定。 判断图5-31中正负穿越的次数