
第4章其于遗传算法的随机优化搜索 第4章基于遗传算法的随机优化搜索 4.1基本概念 4.2基本遗传算法 4.3遗传算法应用举例 4.4遗传算法的特点与优势 习题四 BACK
第 4 章 基于遗传算法的随机优化搜索 第 4 章 基于遗传算法的随机优化搜索 4.1 4.2 基本遗传算法 4.3 遗传算法应用举例 4.4 遗传算法的特点与优势 习题四

第4章基于遗传算法的随机优化搜索 4.1基本概念 1.适应度与适应度函数 适应度(fitness)就是借鉴生物个体对环境的适应程度, 而对所求解问题中的对象设计的一种表征优劣的测度。适应度 函数(fitness function)就是问题中的全体对象与其适应度之 间的一个对应关系,即对象集合到适应度集合的一个映射。 它一般是定义在论域空间上的一个实数值函数
第 4 章 基于遗传算法的随机优化搜索 4.1 基 本概 念 1. 适应度(fitness)就是借鉴生物个体对环境的适应程度, 而对所求解问题中的对象设计的一种表征优劣的测度。适应度 函数(fitness function)就是问题中的全体对象与其适应度之 间的一个对应关系, 即对象集合到适应度集合的一个映射。 它一般是定义在论域空间上的一个实数值函数

第4章其于遗传算法的随机优化搜索 2.染色体及其编码 遗传算法以生物细胞中的染色体(chromosome)代表问题中 的个体对象。而一个染色体可以看作是由若干基因组成的位串, 所以需要将问题中的个体对象编码为某种位串的形式。这样, 原个体对象也就相当于生命科学中所称的生物体的表现型 (phenotypel),而其编码即“染色体”也就相当于生物体的基 因型(genotype)。遗传算法中染色体一般用字符串表示,而基 因也就是字符串中的一个个字符。例如,假设数字9是某问题中 的个体对象,则我们就可以用它的二进制数串1001作为它的染 色体编码
第 4 章 基于遗传算法的随机优化搜索 2. 染色体及其编码 遗传算法以生物细胞中的染色体(chromosome)代表问题中 的个体对象。而一个染色体可以看作是由若干基因组成的位串, 所以需要将问题中的个体对象编码为某种位串的形式。这样, 原个体对象也就相当于生命科学中所称的生物体的表现型 (phenotype), 而其编码即“染色体”也就相当于生物体的基 因型(genotype)。遗传算法中染色体一般用字符串表示, 而基 因也就是字符串中的一个个字符。例如,假设数字9是某问题中 的个体对象, 则我们就可以用它的二进制数串1001作为它的染 色体编码

第4章基于遗传算法的随机优化搜索 3.种群 种群(population)就是模拟生物种群而由若干个染色体组 成的群体,它一般是整个论域空间的一个很小的子集。遗传 算法就是通过在种群上实施所称的遗传操作,使其不断更新换 代而实现对整个论域空间的搜索
第 4 章 基于遗传算法的随机优化搜索 3. 种群 种群(population)就是模拟生物种群而由若干个染色体组 成的群体, 它一般是整个论域空间的一个很小的子集。 遗传 算法就是通过在种群上实施所称的遗传操作,使其不断更新换 代而实现对整个论域空间的搜索

第4章基于遗传算法的随机优化搜索 4.遗传操作 遗传算法中有三种关于染色体的运算:选择-复制、交叉 和变异,这三种运算被称为遗传操作或遗传算子(genetic operator)
第 4 章 基于遗传算法的随机优化搜索 4. 遗传操作 遗传算法中有三种关于染色体的运算: 选择-复制、交叉 和变异,这三种运算被称为遗传操作或遗传算子(genetic operator)

第4章其于遗传算法的随机优化搜索 选择-复制 选择-复制(selection reproduction)操作是模拟 生物界优胜劣汰的自然选择法则的一种染色体运算,就是从种 群中选择适应度较高的染色体进行复制,以生成下一代种群。选 择-复制的通常做法是,对于一个规模为的种群S,按每个染色体 x,∈S的选择概率P(x)所决定的选中机会,分N次从S中随机选定 N个染色体,并进行复制。这里的选择概率Px)的计算公式为 P(x)= f(x) (4-1) ∑f(x,) i-
第 4 章 基于遗传算法的随机优化搜索 选择-复制 选择-复制(selection reproduction)操作是模拟 生物界优胜劣汰的自然选择法则的一种染色体运算, 就是从种 群中选择适应度较高的染色体进行复制,以生成下一代种群。选 择-复制的通常做法是, 对于一个规模为N的种群S,按每个染色体 xi∈S的选择概率P(xi )所决定的选中机会, 分N次从S中随机选定 N个染色体, 并进行复制。 这里的选择概率P(xi )的计算公式为 = = N j j i i f x f x P x 1 ( ) ( ) ( ) (4-1)

第4章其于遗传算法的随机优化搜索 其中,为适应度函数,孔x)为x的适应度。可以看出,染色体 x,被选中的概率就是其适应度x)所占种群中全体染色体适应 度之和的比例。显然,按照这种选择概率定义,适应度越高的 染色体被随机选定的概率就越大,被选中的次数也就越多,从 而被复制的次数也就越多。相反,适应度越低的染色体被选中 的次数也就越少,从而被复制的次数也就越少。如果把复制看 做染色体的一次换代的话,则这就意味着适应度越高的染色体 其后代也就越多,适应度越低的染色体其后代也就越少,甚至被 淘汰。这正吻合了优胜劣汰的自然选择法则
第 4 章 基于遗传算法的随机优化搜索 其中,f为适应度函数,f(xi )为xi的适应度。可以看出, 染色体 xi被选中的概率就是其适应度f(xi )所占种群中全体染色体适应 度之和的比例。 显然, 按照这种选择概率定义, 适应度越高的 染色体被随机选定的概率就越大, 被选中的次数也就越多, 从 而被复制的次数也就越多。相反,适应度越低的染色体被选中 的次数也就越少,从而被复制的次数也就越少。如果把复制看 做染色体的一次换代的话,则这就意味着适应度越高的染色体 其后代也就越多,适应度越低的染色体其后代也就越少, 甚至被 淘汰。 这正吻合了优胜劣汰的自然选择法则
第4章基于遗传算法的随机优化搜索 西安地子科发大之常版在 西交地 西安地子利数大 西来地 孝欢收羽 S2 0.45 Su 0.11 S4 S3 电 0.15 0.29 西安电 图4-1赌轮选择示例
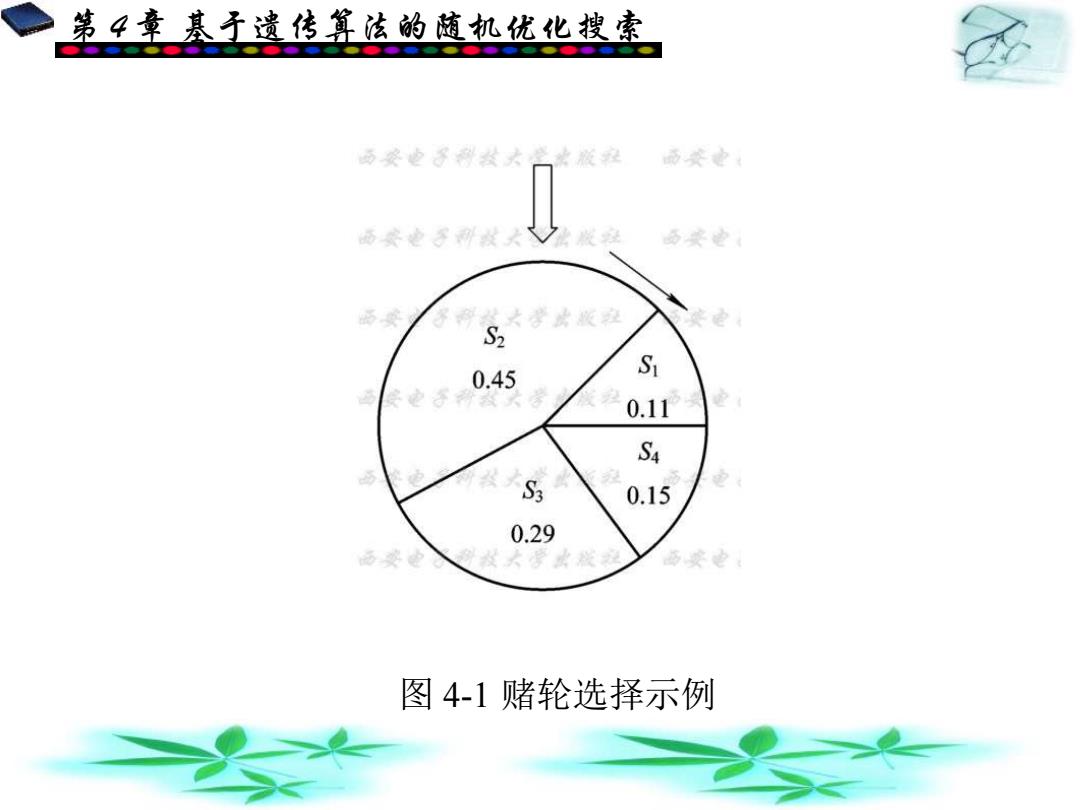
第 4 章 基于遗传算法的随机优化搜索 图 4-1 赌轮选择示例

第平章基于遗传算法的随机优化搜索 上述按概率选择的方法可用一种称为赌轮的原理来实现。 即做一个单位圆,然后按各个染色体的选择概率将圆面划分 为相应的扇形区域(如图4-1所示)。这样,每次选择时先转动 轮盘,当轮盘静止时,上方的指针所正对着的扇区即为选中的 扇区,从而相应的染色体即为所选定的染色体。例如,假设种 群S中有4个染色体:S1S2S3,S4,其选择概率依次为:0.11,0.45, 0.29,0.15,则它们在轮盘上所占的份额如图4一1中的各扇形 区域所示
第 4 章 基于遗传算法的随机优化搜索 上述按概率选择的方法可用一种称为赌轮的原理来实现。 即做一个单位圆, 然后按各个染色体的选择概率将圆面划分 为相应的扇形区域(如图4-1所示)。这样, 每次选择时先转动 轮盘, 当轮盘静止时,上方的指针所正对着的扇区即为选中的 扇区,从而相应的染色体即为所选定的染色体。 例如, 假设种 群S中有4个染色体: s1 ,s2 , s3 , s4 ,其选择概率依次为: 0.11, 0.45, 0.29, 0.15, 则它们在轮盘上所占的份额如图4-1中的各扇形 区域所示

第4章基于遗传算法的随机优化搜索 在算法中赌轮选择法可用下面的子过程来模拟: ①在[0,1]区间内产生一个均匀分布的伪随机数r。 ②若≤91,则染色体x,被选中。 ③若qk-1<9(2≤N),则染色体x被选中。 其中的qg称为染色体x,(=1,2,.,n)的积累概率,其计算公式 为 q,=∑P(x) i_1
第 4 章 基于遗传算法的随机优化搜索 在算法中赌轮选择法可用下面的子过程来模拟: ① 在[0, 1]区间内产生一个均匀分布的伪随机数r。 ② 若r≤q1 ,则染色体x1被选中。 ③ 若qk-1<r≤qk (2≤k≤N), 则染色体xk被选中。 其中的qi称为染色体xi (i=1, 2, …, n)的积累概率, 其计算公式 为 = = i j i j q P x 1 ( )