自动控荆原理 第五章 频域分析法一频率法 第五章 线性系统的频域分析法 频域分析法是研究自动控制系统的一种工程方法, 它能反映不同频率的正弦信号作用下系统的性能。 5.1频率特性 一、基本概念 系统
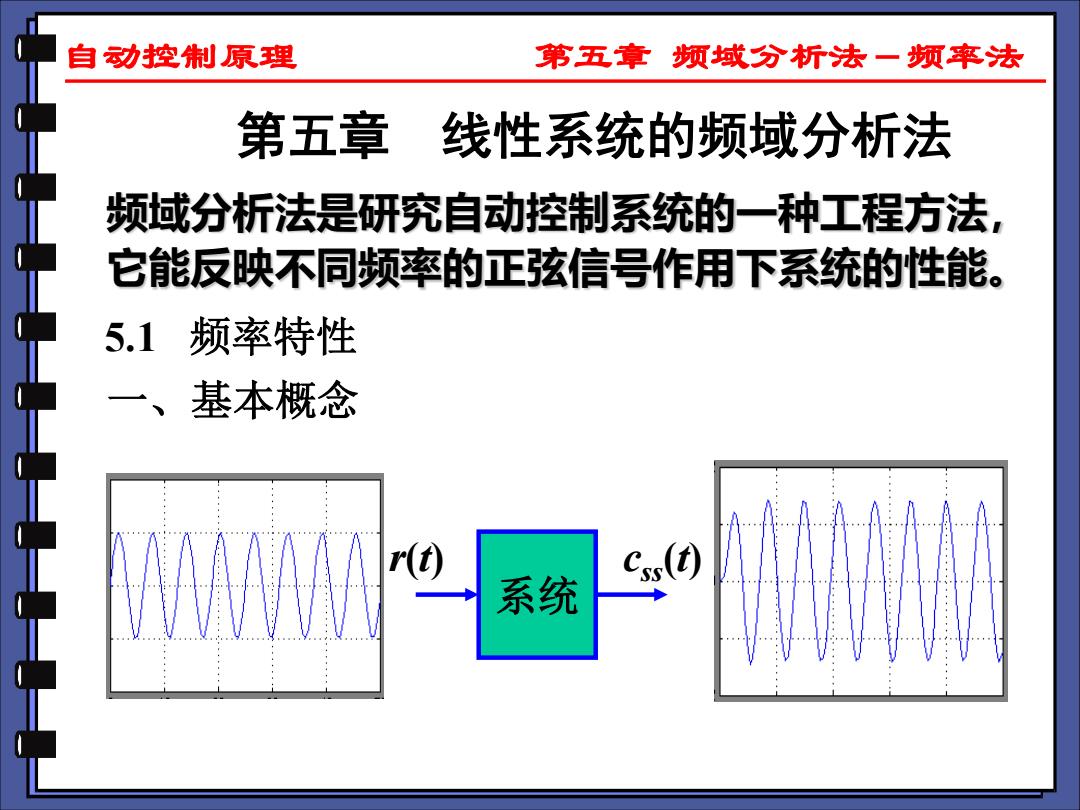
自动控制原理 第五章 频域分析法-频率法 第五章 线性系统的频域分析法 5.1 频率特性 一、基本概念 系统 r(t) css(t) 频域分析法是研究自动控制系统的一种工程方法, 它能反映不同频率的正弦信号作用下系统的性能

自动控原理 第五章 领域分析法一频率法 个稳定的系统,假设有一正弦信号输入 r(t)=A.sinot 其稳态输出可写为 A。-稳态输出的振幅 Css(t)=A。sin(ot+pj ⑩-稳态输出的相角 稳态输出的振幅与输入振幅之比,称为幅频特性。 稳态输出的相位与输入相位之差0,称为相频特性。 称为频率特性
自动控制原理 第五章 频域分析法-频率法 稳态输出的振幅与输入振幅之比,称为幅频特性。 稳态输出的相位与输入相位之差,称为相频特性。 c r A A A = 一个稳定的系统,假设有一正弦信号输入 r r t A t ( ) sin = 其稳态输出可写为 ss c c t A t ( ) sin( ) = + Ac --稳态输出的振幅 --稳态输出的相角 A 称为频率特性
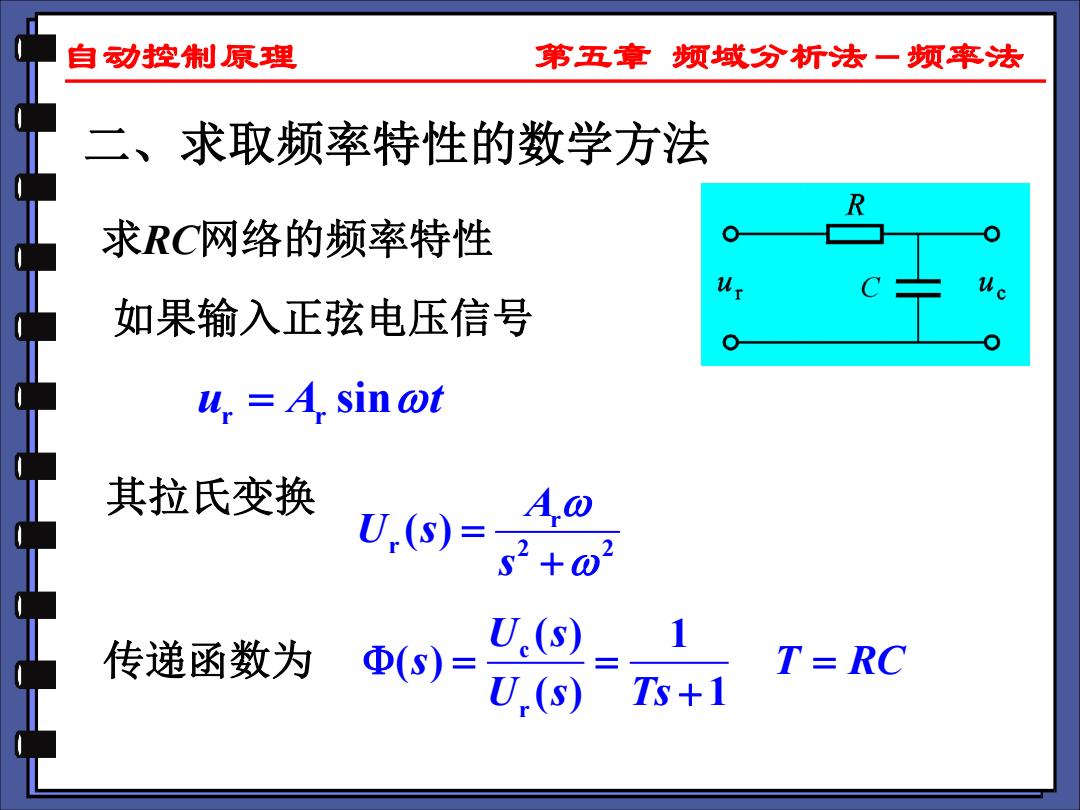
自动控荆原理 第五章频域分析法一频率法 二、求取频率特性的数学方法 求RC网络的频率特性 如果输入正弦电压信号 u,=A,sin @t 其拉氏变换 A@ U,)=s2+02 传递函数为 Φ(S)= U.(S) T=RC U.(s) Ts+1
自动控制原理 第五章 频域分析法-频率法 二、求取频率特性的数学方法 求RC网络的频率特性 c r ( ) 1 ( ) ( ) 1 U s s T RC U s Ts = = = + 如果输入正弦电压信号 r r u A t = sin 其拉氏变换 r r 2 2 ( ) A U s s = + 传递函数为

自动控原理 第五章频域分析法一频率法 所以系统的输出为 8=oc0)不4140 拉氏反变换为 A@T A I+o'Tie 十 sin(@t-arctan @T) 1+@'T2 式中第一项为动态分量,第二项为稳态分量。 mo0=+7 sin(@t-arctan @T)
自动控制原理 第五章 频域分析法-频率法 所以系统的输出为 r c r 2 2 1 ( ) ( ) ( ) 1 A U s s U s Ts s = = + + 拉氏反变换为 r r c 2 2 2 2 ( ) e sin( arctan ) 1 1 t T A T A u t t T T T − = + − + + 式中第一项为动态分量,第二项为稳态分量。 r c 2 2 lim ( ) sin( arctan ) 1 t A u t t T T → = − +

自动控原理 第五章频域分析法一频率法 稳态输出: u,A.sin ot sin(O arctan @l 幅频特性:A(@)=1+02T2 二者仅是频率的函数 相频特性:p(o)=-arctan @T 频率特性: G(s)j=G(j@)=A(@)Lp(@)
自动控制原理 第五章 频域分析法-频率法 稳态输出: r c 2 2 lim ( ) sin( arctan ) 1 t A u t t T T → = − + 幅频特性: 相频特性: 2 2 1 ( ) 1 A T = + ( ) arctan = − T 二者仅是频率的函数 频率特性: ( ) ) ( ( ) ( ) s j G s G j A = = = r r u A t = sin
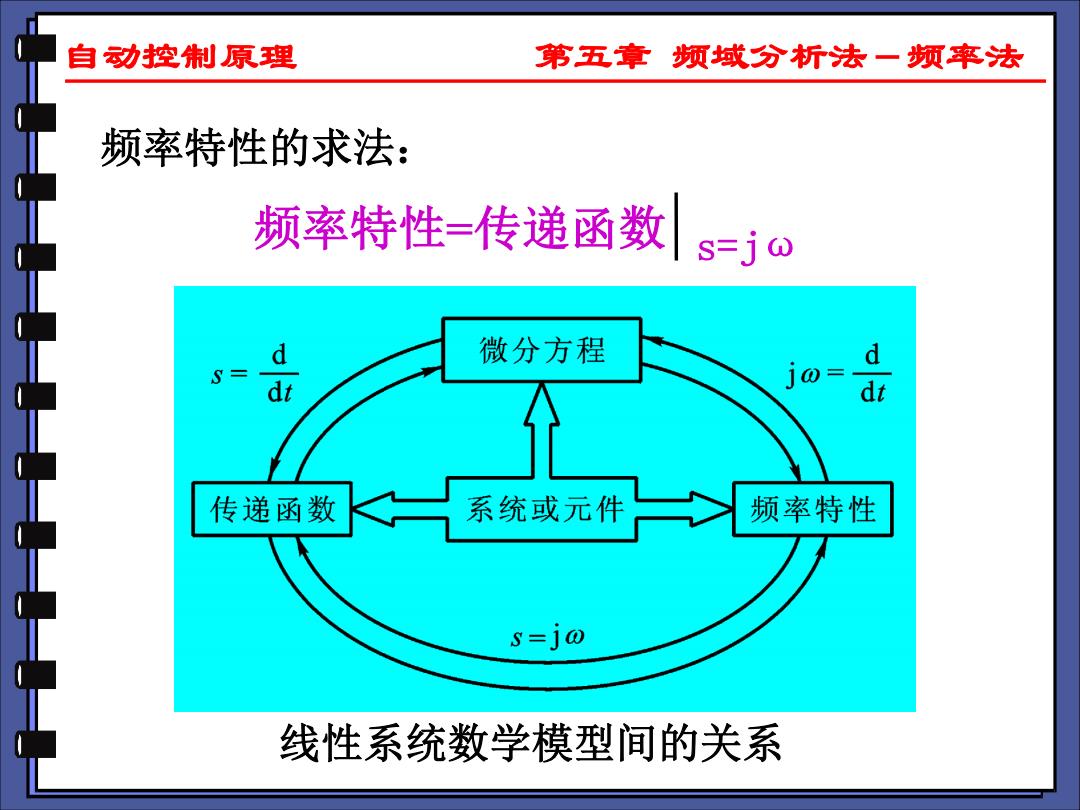
自动控荆原理 第五章频域分析法一频率法 频率特性的求法 频率特性=传递函数 s=jw 微分方程 d j0= d 传递函数 系统或元件 频率特性 s-j@ 线性系统数学模型间的关系
自动控制原理 第五章 频域分析法-频率法 频率特性的求法: 频率特性=传递函数 s=jω 线性系统数学模型间的关系

自动控荆原理 第五章 频域分折法一频率法 1 补例设系统的传递函数为 G(S)= 0.5s+1 试求输入信号r(t)=10sin2t 时,系统的稳态 输出c小. 解:系统频率特性为 1 G(jω)= ∠-arctan0.5o 0.5w+1 /0.2502+1 当频率0=2时, 60j2)=a4-45e 故系统的稳态输出为 c.④=10x sin(2t-45)
自动控制原理 第五章 频域分析法-频率法 • 补例 设系统的传递函数为 • 试求输入信号 时,系统的稳态 输出c ss(t). 1 ( ) 0.5 1 G s s = + r t t ( ) 10sin 2 = 解:系统频率特性为 2 1 1 ( ) arctan 0.5 0.5 1 0.25 1 G j j = = − + + 当频率ω=2时, 1 ( 2) 45 2 G j = − 故系统的稳态输出为 1 ( ) 10 sin(2 45 ) 2 ss c t t = −
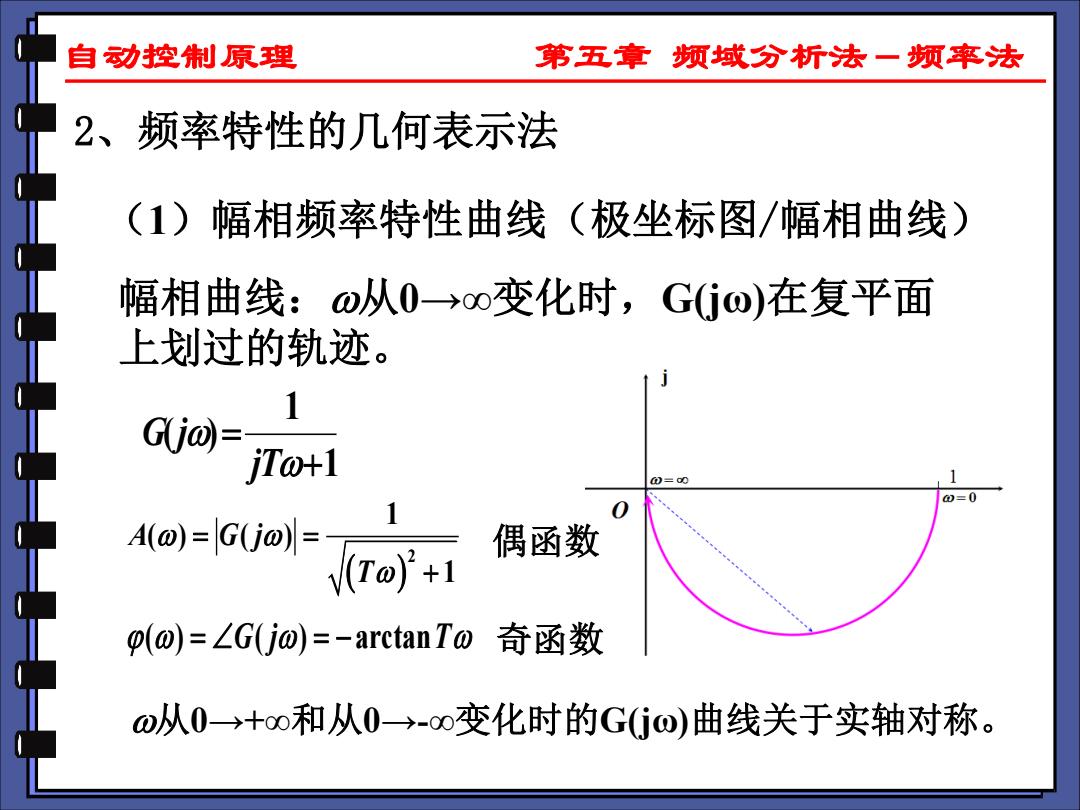
自动控制原理 第五章频域分析法一频率法 2、 频率特性的几何表示法 (1)幅相频率特性曲线(极坐标图/幅相曲线) 幅相曲线:o从0→oo变化时,GGjo)在复平面 上划过的轨迹。 G(j0= iT@+1 0=a0 Ae)-ca-T 偶函数 (@)=ZG(jo)=-arctanTo 奇函数 o从0→+o0和从0→-o变化时的G(G@)曲线关于实轴对称
自动控制原理 第五章 频域分析法-频率法 2、频率特性的几何表示法 (1)幅相频率特性曲线(极坐标图/幅相曲线) 幅相曲线:从0→∞变化时,G(jω)在复平面 上划过的轨迹。 1 ( ) 1 G j jT = + ( ) 2 1 ( ) ( ) 1 A G j T = = + ( ) ( ) arctan = = − G j T 偶函数 奇函数 从0→+∞和从0→-∞变化时的G(jω)曲线关于实轴对称
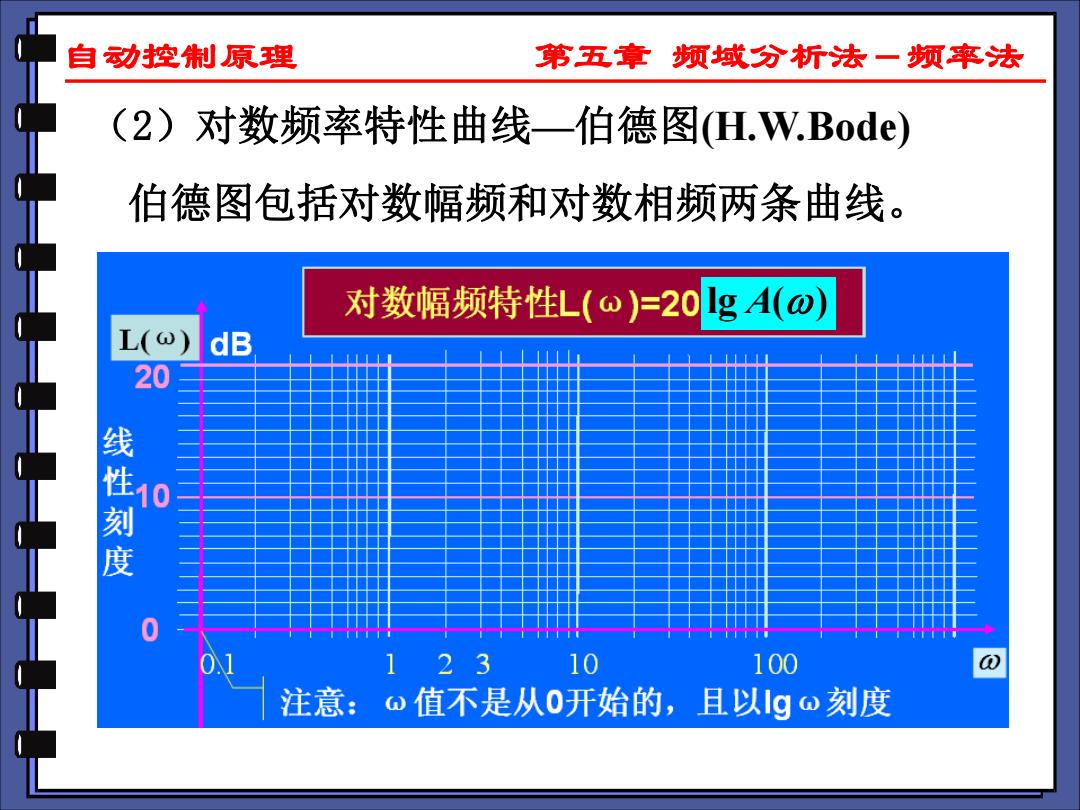
自动控制原理 第五章 频域分析法一频率法 (2)对数频率特性曲线一伯德图H.W.Bode) 伯德图包括对数幅频和对数相频两条曲线。 对数幅频特性L(o)=201gA(ω)》 L() dB 20 线性刻度 123 10 100 注意:⊙值不是从0开始的,且以Igo刻度
自动控制原理 第五章 频域分析法-频率法 (2)对数频率特性曲线—伯德图(H.W.Bode) 伯德图包括对数幅频和对数相频两条曲线。 lg ( ) A
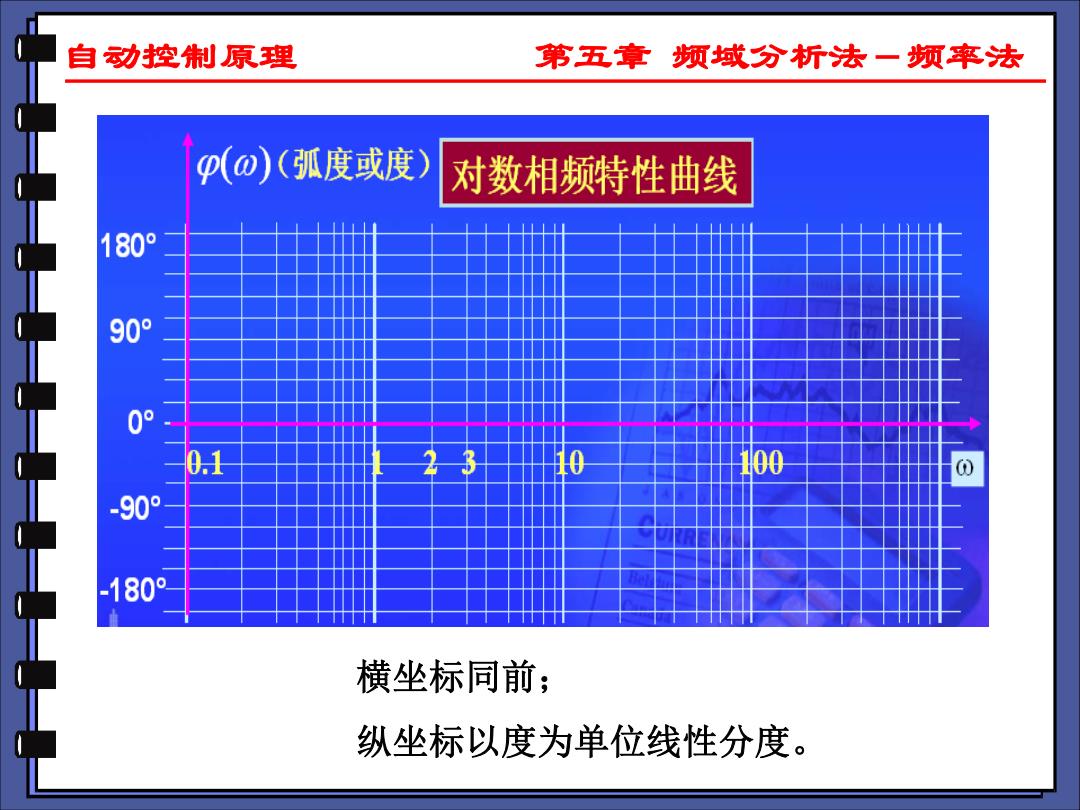
自动控原理 第五章频域分析法一频率法 (⊙)(弧度或度 对数相频特性曲线 180° 90 0° 0.1 230 100 -90° 180° 横坐标同前; 纵坐标以度为单位线性分度
自动控制原理 第五章 频域分析法-频率法 横坐标同前; 纵坐标以度为单位线性分度