
细台形z幸院 antai Institute of Technology 原城台好火维年院 第五章速度和静力 四5.1时变位置和姿态的符号表示 四5.2刚体的线速度和角速度 四5.3机器人连杆的运动 四5.4雅可比矩阵 四5.5机械臂中的静力 2
2 5.1 时变位置和姿态的符号表示 5.2 刚体的线速度和角速度 5.3 机器人连杆的运动 5.4 雅可比矩阵 5.5 机械臂中的静力 第五章 速度和静力

细台程2幸优 antai Institute of Technology 时变位置和姿态的符号表示 原城台好父维年能 >位置失量PQ的微分 BVQ二dt BPo(t+At)-BPo(t) △t-→0 △t 位置失量BPo相对于坐标系B}的微分 0=是 表达在坐标系{A)中 =BRB(BVQ)=BRBVO 当两个坐标系是同一个坐标系时 UVC ORG 坐标系{C}的原点相对于世界参考坐标系的速度
3 时变位置和姿态的符号表示 Ø 位置矢量 的微分 位置矢量 相对于坐标系{B}的微分 表达在坐标系{A}中 当两个坐标系是同一个坐标系时 坐标系{C}的原点相对于世界参考坐标系的速度
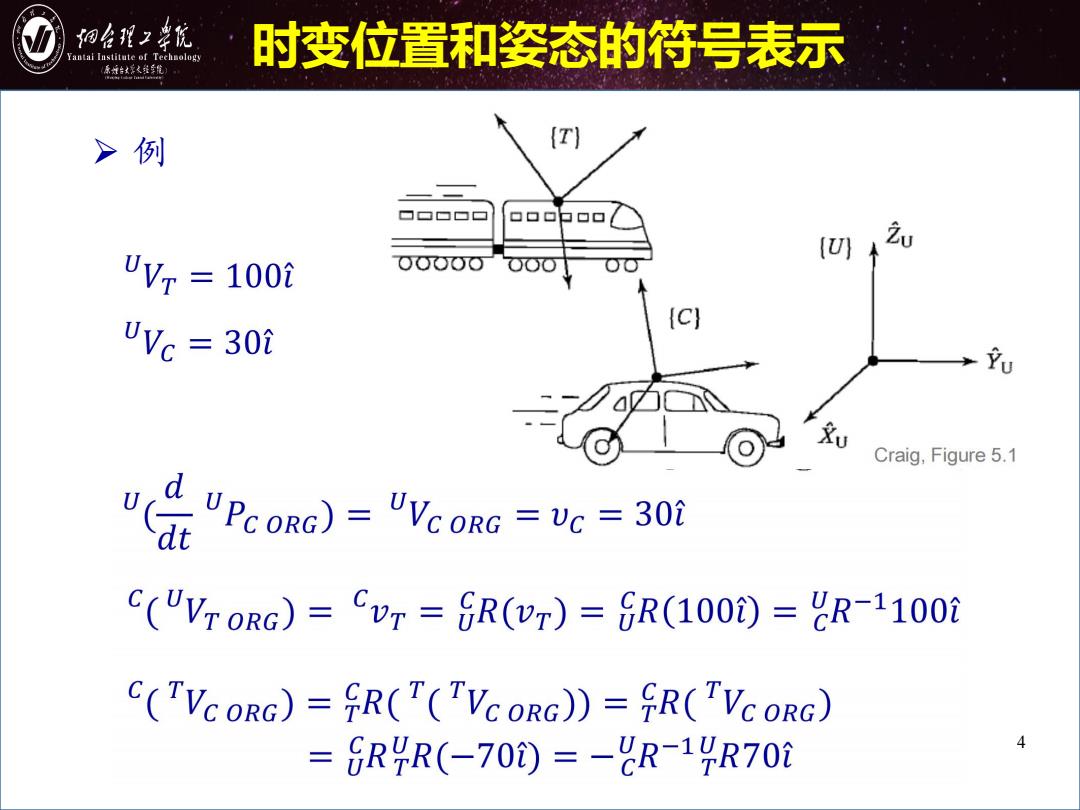
细台程2幸优 antai Institute of Technology 时变位置和姿态的符号表示 原城台好火维年馆 >例 (T □口口口口 (U) 1000 0000o UVc 30i [c] u Craig,Figure 5.1 d UPcORG)=VVeORG-vc=30 v(at C("V7oRG)=Cv7=R(r)=R(100)=&R-1100i C(TVCORG)=fR(T(TVCORG))=fR(VCORG) = SRR(-70)=-光R-14R70i 4
4 时变位置和姿态的符号表示 Ø 例

细台程2幸优 antai Institute of Technology 时变位置和姿态的符号表示 原城台家之维能 >角速度夫量A2B ◆坐标系{B)相对于坐标系{A的转动 ◆ A2B的方向:瞬时的旋转轴 A2g的大小:旋转的速度 B {A} C(AOB) 在坐标系(C)的表达 wc USc 坐标系{C)相对于世界参考坐标 系{U}的角速度。 5
5 时变位置和姿态的符号表示 Ø 角速度矢量 u坐标系{B}相对于坐标系{A}的转动 u 的方向:瞬时的旋转轴 u 的大小:旋转的速度 在坐标系{C}的表达 坐标系{C}相对于世界参考坐标 系{U}的角速度

细台形2幸院 antai Institute of Technology 刚体的运动 原城台好火维年馆 >线速度失量 TA=xAI+yAJ A TB TA/B =(xBI+yB])+(XA/Bi+ya/Bj) TA/B X =TB +TA/B Y B =(xBi+yB])+(xa/Bi+yA/Bj) diff. U仍 TB Z X VA TA=XA1+yAJ =亩+TA/B Z =(xBI+yB])+(XA/BI+yA/BJ) 6
6 刚体的运动 Ø 线速度矢量

阳台理:华优 antai Institute of Technology 刚体的运动 原城台好火维年航 A=馆+AB =(xB1+yB])+(xi/Bi+yi/Bi)+(xA/B i+yA/Bj) =xA/B(⑥×)+yA/B(而×) 1o1=0 Magnitude: ldel lelsingde e=lelsinge=lellulsin lel sin Direction: de⊥e de⊥ e(t+△t) 〉è=0×e 7
7 刚体的运动
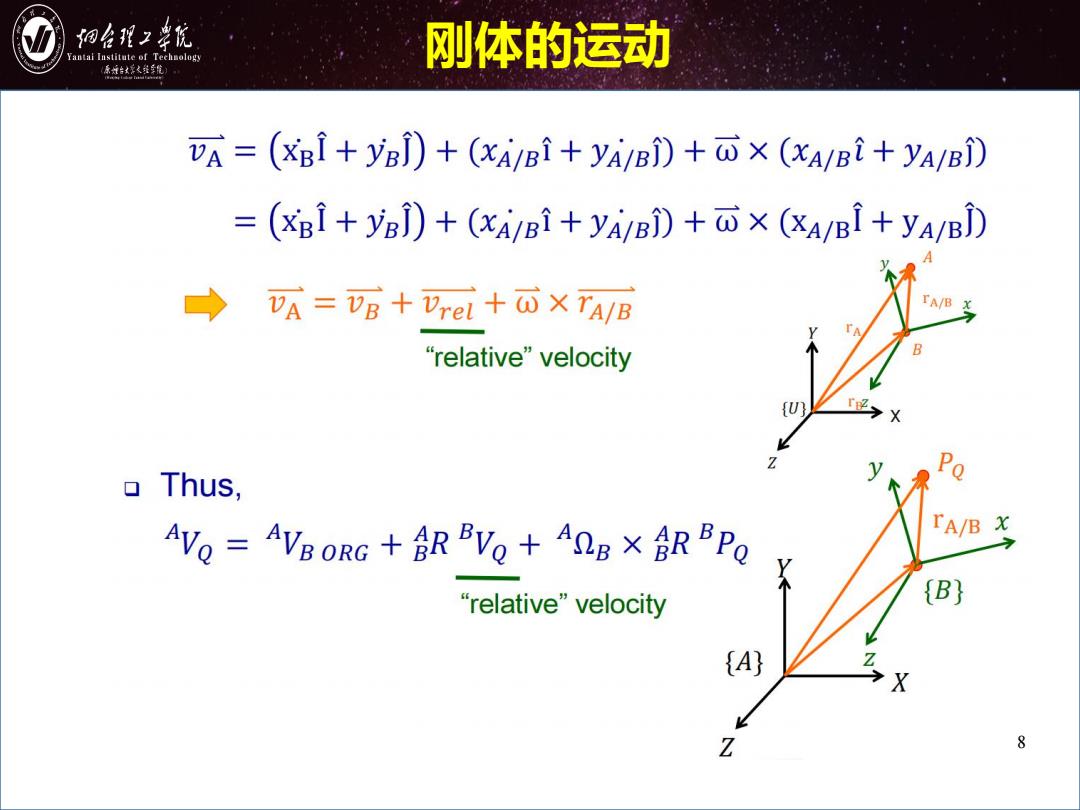
细台形2幸院 antai Institute of Technology 刚体的运动 原城台家父维缆 VA=(xBi+yB])+(xi/Bi+yi/Bi)+x (xA/Bi+yA/B) =(XB1+yB)+(xA/B1+yABi)+而×(&A/Bi+yA/B) → a=店+re+西XTA/B A/B “relative”velocity o Thus, Po AVo AVB ORG+R Vo+AQB xR Po TA/B x “relative”velocity (B) (A} X Z 8
8 刚体的运动

细台程2幸优 antai Institute of Technology 速度在连杆之间的传递 原城台好火维年院 >策略:已知连杆i在坐标系{}中的线速度和角速度, 找到它们和相邻连杆之间的速度和角速度的关系。 Axis i+1 Axis i i*10*1 i01 2+1 1+1D1+1 Link i iPirl Xi+1 0 L0+1 9
9 速度在连杆之间的传递 Ø 策略:已知连杆i在坐标系{i}中的线速度和角速度, 找到它们和相邻连杆之间的速度和角速度的关系
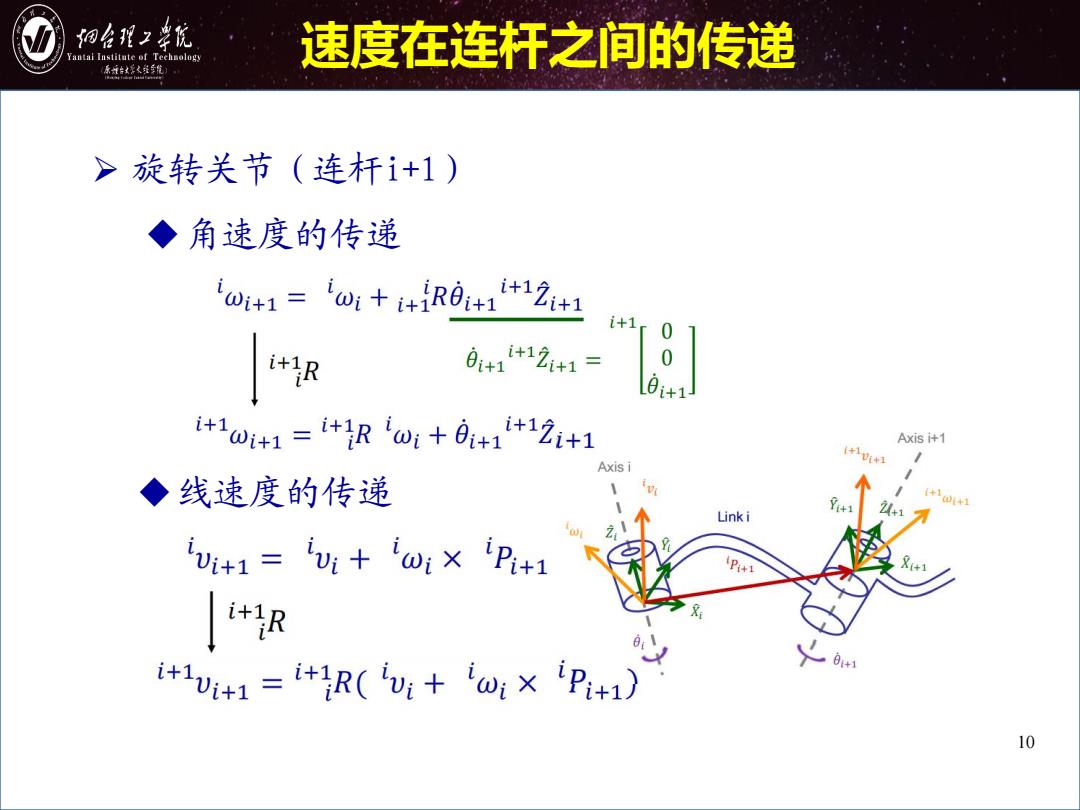
细台程2幸优 Yantai Institute of Technology 速度在连杆之间的传递 原城台文家之维单能 >旋转关节(连杆i+1) ◆角速度的传递 w+1=iw+i+iR0+1+12+ i+1 0 0+1+12+1= 0 0+1 +1ω+1=i+Rw:+0+1+12+1 Axis i+1 Axis i +1*1 ◆线速度的传递 *1 2认17 +10*1 Linki vi+1=v+ωi×P+1 P*1 +R i+1v+1=i+1R(u:+w:×P+1) 0+1 10
10 速度在连杆之间的传递 Ø 旋转关节(连杆i+1) u角速度的传递 u线速度的传递
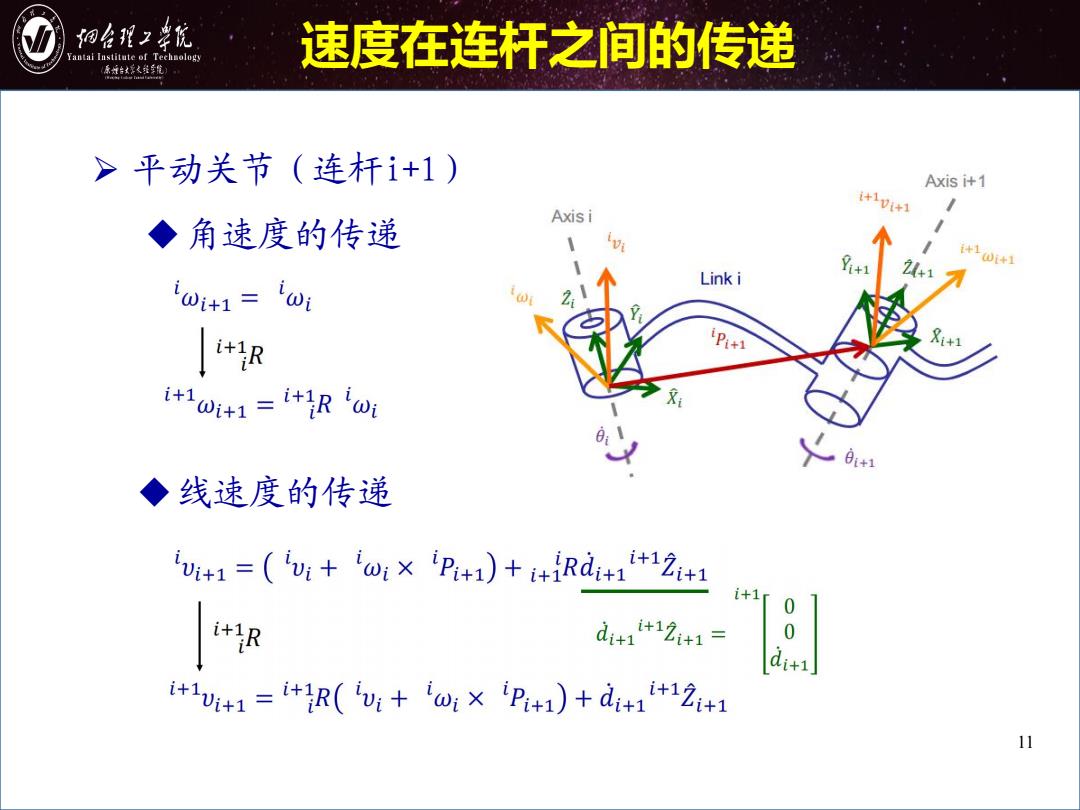
细台程2幸优 Yantai Institute of Technology 速度在连杆之间的传递 原城台大家之维单能 >平动关节(连杆i+1) Axis i+1 Axis i *10*1 ◆角速度的传递 2*17 计10*1 twi=wr Link i |+R i+ i+1w+1=i+Rω 0+1 ◆线速度的传递 u+1=(+w×ip+i)+i+iRd+1+12+1 0 R d+112+1= 0 i+1u+1=i+R(u+w×P+1)+d+1+12+1 11
11 速度在连杆之间的传递 Ø 平动关节(连杆i+1) u角速度的传递 u线速度的传递